Вопрос №1. Электрическое смещение. Поток смещения.

Лекция № 4

Расчет полей заданных электрических зарядов

План лекции:

1. Электрическое смещение. Поток смещения.

2. Теорема Гаусса для электрического поля в диэлектрике.

3. Расчет поля равномерно заряженных бесконечных плоскостей.

4. Напряженность и потенциал поля равномерно заряженной сферической поверхности.

5. Напряженность и потенциал поля объемно заряженного шара.

6. Напряженность и потенциал заряженных цилиндра, бесконечной прямой нити.

 

 

Вопрос №1. Электрическое смещение. Поток смещения.

Для описания электростатического поля используют его силовую характеристику — напряженность поля Е. Эта величи­на зависит от свойств среды, которые определяются диэлектрической проницаемо­стью е в выражении:

.

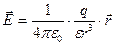В диэлектрической среде напряженность поля определя­ется как свободными, так и связанными зарядами.

Связанными зарядами называются заряды, которые входят в состав атомов и молекул, а также заряды ионов в кристалли­ческих диэлектриках с ионной решеткой. Свободные заряды — это заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электроны проводимости в металлах и полупроводниках, электроны в ва­кууме, ионы в электролитах и ионизированных газах). К свободным относятся также избыточные заряды, сообщаемые телу и нарушающие его электростатическую ней­тральность (например, заряды, нанесенные извне на поверхность диэлектрика).

Чтобы при описании поля в изотропной среде (диэлектрике) скомпенсировать влияние этой среды на напряженность Е (Е = Ео / ε), вводят дополнительную характе­ристику поля, называемую электрическим смещением 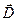(прежнее название — элек­трическая индукция):

(1.1)

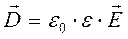
В случае точечного заряда проекция вектора 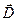на направ­ление радиус-вектора 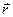определяется по формуле

(1.2)

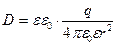откуда следует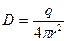

Из выражения (1.2) видно, что электрическое смещение 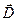не зависит от электриче­ской проницаемости ε среды и определяется только свободным зарядом q. Оно измеряется в тех же единицах, что и поверхностная плотность σ заряда, т.е. [D] = 1 Кл/1 м².

Рис 1.

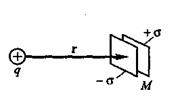
Элек­трическое смещение в определенной небольшой области пространства можно измерить с помощью «пластинок Ми», которые представляют собой обкладки плоского конден­сатора. Если расположить эти пластинки на некотором расстоянии r от точечного заряда q и сориентировать так, чтобы их плоскость была перпендикулярна вектору 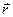(рис. 1.), то плотность заряда σ, индуцированного на одной из пластинок, будет численно равна электрическому смещению D, создаваемому зарядом q в точке М.

 

 

Из выражения (1.2) видно, что электрическое смещение фактически характери­зует интенсивность поля, создаваемого только свободными зарядами. Так же как и на­пряженность Е, электрическое смещение D удовлетворяет принципу суперпозиции.

Аналогично вводят линии электрического смещения, направление и густота которых удовлетворяют тем же правилам, которые справедливы для линий напряженности.

Для расчета электростатических полей большое значение имеет поток электриче­ского смещения Ф, который вводится следующим образом.

Рис. 2.

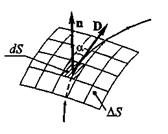
Пусть имеется небольшая произвольно ориентированная поверхность Δ S, расположенная в электрическом поле (рис. 2).

 

 

(1.3)

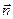Разобьем ее произвольным образом на элементарные площадки dS, к каждой из которых проведем вектор нормали . Тогда элементарным потоком вектора смеще­ния 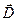, пронизывающим площадку dS, называется величина d Ф = D · ndS = DdS ·cos a = = D_n · dS, a значение потока через всю поверхность dS получим интегрированием:

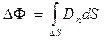
В дальнейшем для расчета характеристик поля, т.е. смещения D и напряженности Е, нам понадобится поток D сквозь замкнутую поверхность S в направлении внешней нормали к этой поверхности:

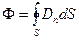- определение потока вектора D.