Пусть А – случайное событие по отношению к некоторому испытанию. Представим себе, что это испытание произведено N раз и при этом событие А наступило в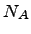 
случаях. Тогда отношение
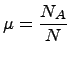называется частотой события А в данной серии испытаний.
Определение. Вероятностью случайного события А называется число 
, около которого колеблется частота этого события в длинных сериях испытаний.
Случайное событие является следствием очень многих обстоятельств, точно учесть которые невозможно. Теория вероятностей не отвечает на вопрос, произойдет или не произойдет некоторое единичное случайное событие. Например, если один раз бросить монету, то нельзя сказать, упадет она «гербом» кверху или нет. Если же бросить монету 1000 раз, то примерно 500 раз появится «герб».
Пусть есть некоторое событие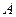 
. Производится 
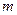опытов. В числе опытов 
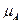событие 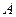имеет место. Допустим, что предел 
существует. Тогда он называется вероятностью события :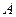
.
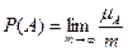При помощи статистического определения можно получить вероятность любого события.
Недостатком статистического определения вероятности является неоднозначность статистической вероятности; так в примере с бросанием монеты в качестве вероятности можно принять не только число 0,5, но и 0,49 или 0,51 и т.д. Для надежного определения вероятности нужно проделать большое число испытаний (опытов), что не всегда просто.
При неоднократном повторении испытаний наблюдаются закономерности, свойственные массовым случайным явлениям. Эти закономерности обладают свойством устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными.
Пусть производится большая серия однотипных опытов. Исход каждого отдельного опыта является случайным, неопределенным. Однако, несмотря на это, средний результат всей серии опытов утрачивает случайный характер, становится закономерным.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел.
Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.
К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим.
В основе доказательства теорем, объединенных термином "закон больших чисел", лежит неравенство Чебышева, по которому устанавливается вероятность отклонения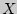 
от ее математического ожидания:
Теорема Бернулли. Если в каждом из 
независимых испытаний вероятность 
появления события 
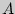постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если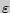 
сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство
При доказательстве теоремы Бернулли получаем оценку
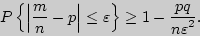
Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности
Алгебра событий.
Событие, относящиеся к результату некоторого испытания (эксперимента), которое может при наличии некоторого комплекса условий S произойти или не произойти, называется случайным событием.
Событие, которое в результате испытания
– наступит всегда, называется достоверным событием;
– не наступит никогда, называется невозможным событием.
Случайные события будут обозначаться буквами A, B, C, …; достоверные – Ω, невозможные – ∅.
Суммой двух событий A и B называется событие C = A + B, (или иначе, C = A ∪ B), которое произойдет, если произошло хотя бы одно из этих событий A или B (рис. 1.1).
Произведением двух событий A и B называется событие C = A ⋅ B, (или C = A ∩ B), которое произойдет, если произошли оба события A и B (рис. 1.2).
Разностью двух событий A и B называется событие C = A – B (или C = A \ B), которое произойдет, если произошло событие A, но не произошло событие B (рис. 1.3).
А В А В А В
Рис. 1.1 A + B Рис. 1.2 A ⋅ B Рис. 1.3 A \ B
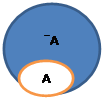
Событие⎯A = Ω \ A называется противоположным событию A, если оно наступает тогда и только тогда, когда не происходит событие A (рис. 2.1).
Если каждое появление события A влечет за собой появление события B, то говорят, что из A следует B, и пишут: A ⊂ B (рис. 2.2). Если одновременно имеют место соотношения A ⊂ B и B ⊂ A, то события A и B называют равносильными. События называются несовместными в данном испытании, если они не могут произойти вместе, т.е. A ⋅ B = ∅.
 | |||
 | |||
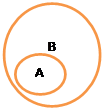Рис. 2.1 Событие A. Рис. 2.2 A ⊂ B
Полной группой событий называются такие события А, В, С, …, что при всякой реализации комплекса условий S хотя бы одно из них обязательно происходит, то есть А+В+С+…= Ω.
Действия над событиями могут быть проиллюстрированы с помощью диаграмм Bенна, которые и представлены на рис.1 и 2.
