Лекція 23
Тема: Числові ряди.
Основні поняття
Нескінченні ряди широко використовуються в теоретичних дослідженнях математичного аналізу, мають різноманітні практичні застосування.
Числовим рядом (або просто рядом) називається вираз вигляду
(1)
де 
дійсні або комплексні числа, які називають членами ряду, 
- загальним членом ряду.
Ряд (1) вважається заданим, якщо відомий загальний член ряду 
виражений як функція його номера 
.
Сума перших 
членів ряду (1) називається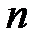 
-ою частинною сумою ряду і позначається через 
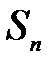, тобто 
. Розглянемо часткові суми
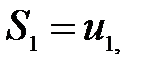
Якщо існує кінцева границя 
послідовності часткових сум ряду (1), то цю границю називають сумою ряду (1) і говорять, що ряд збігається. Записують: 
. 
Якщо 
не існує або 
, то ряд (1) називають тим, що розбіжний. Такий ряд суми не має.
Розглянемо приклади:
1. Ряд 2 + 17 - 
+ 196 +... не можна вважати заданим, а ряд 2 + 5+8 +... — можна: його загальний член задається формулою 
2. Ряд 0 + 0 + 0 +... + 0 +... збігається, його сума дорівнює 0.
3. Ряд 1 + 1 + 1 +... + 1 +... розбіжни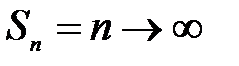й 
при 
4. Ряд 1 – 1 + 1 –1 + 1 – 1 +... розбіжний, оскільки послідовність, частинних сум 1,0,1,0,1,0...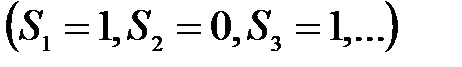 
не має границі.
5. Ряд 
збігається. Дійсно,
……………………,
Отже, 
тобто ряд збігається, його сума дорівнює 1.
Властивість 1. Якщо ряд (1) збігається і його сума дорівнює 
, то ряд
(2)
де с – довільне число, також збігається і його сума дорівнює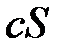 
. Якщо ж ряд (1) розбіжний і 
, то і ряд (2) розбіжний.
Позначимо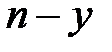 
частинну суму ряду (2) через 
. Тоді
.
Отже, 
тобто ряд (2) збігається і має суму 
Покажемо тепер, що якщо ряд (1) розбіжний 
, то і ряд (2) розбіжний. Припустимо протилежне: ряд (2) збігається і має суму 
.
Тоді 
Звідси отримуємо: 
тобто ряд (1) збігається, що суперечить умові про розходження ряду (1).
Властивість 2. Якщо збігається ряд (1) і збігається ряд
(3)
а їх суми дорівнюють 
і 
відповідно, то збігаються і ряди
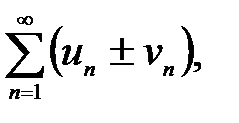(4)
причому сума кожного дорівнює відповідно 
.
Позначимо 
частинні суми рядів (1), (3) і (4) через 
, 
і 
відповідно. Тоді 
тобто кожний з рядів (4) збігається, і сума його дорівнює 
відповідно.
З властивості 1 витікає, що сума (різниця) рядів, що збігаються і рядів, що розбіжні є ряд, що розбіжний.
В справедливості цього твердження можна переконатися методом від протилежного.
Відзначимо, що сума (різниця) двох рядів, що розбіжні, може бути як рядом, що збігається, так і рядом, що розбіжний.
Властивість 3. Якщо до ряду (1) додати (або відкинути) кінцеве число членів, то отриманий ряд і ряд (1) збігаються або розбіжні одночасно.
Позначимо через 
суму відкинутих членів, через 
— найбільший з номерів цих членів. Щоб не змінювати нумерацію членів ряду (1), що залишилися, вважатимемо, що на місці відкинутих членів поставили нулі. Тоді при п > 
виконуватиметься рівність 
де 
— це п-а частинна сума ряду, отриманого з ряду (1) шляхом відкидання кінцевого числа членів. Тому 
. Звідси випливає, що границі в лівій і правій частинах одночасно існують або не існують, тобто ряд (1) збігається (розбіжний) тоді і тільки тоді, коли збігаються (розбіжні) ряди без кінцевого числа його членів. Аналогічно міркуємо у разі приписування до ряду кінцевого числа членів.
Ряд 
(5) називається 
-ою остачею ряду (1). Він отримується з ряду (1) відкиданням п перших його членів. Ряд (1) виходить із остачі додаванням кінцевого числа членів. Тому, згідно властивості 3, ряд (1) і його остача (5) одночасно збігаються або розбіжні.
З властивості 3 також випливає, що якщо ряд (1) збігається, то його остача 
прямує до нуля при 
, тобто 
Ряд геометричної прогресії. Дослідимо збіжність ряду
(
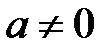), (6)
який називається рядом геометричної прогресії. Ряд (6) часто використовується при дослідженні рядів на збіжність.
Як відомо, сума перших 
членів прогресії знаходиться по формулі 
. Знайдемо границю цієї суми:
Розглянемо наступні випадки в залежності від величини 
1. Якщо |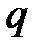 
| < 1, то 
при 
. Тому 
ряд (6) збігається, його сума дорівнює 
2. Якщо | 
| > 1, то 
при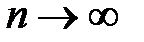 
. Тому 
, ряд (6) розбіжний;
3. Якщо | 
| = 1, то при 
= 1 ряд (6) приймає вигляд 
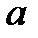+ а + 
+... + 
+..., для нього 
і 
, тобто ряд (6) розбіжний; при 
= - 1 ряд (6) приймає вигляд а - 
- в цьому випадку 
= 0 при парному п і 
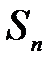= а при непарному п. Отже, 
не існує, ряд (6) розбіжний.
Отже, ряд геометричної прогресії збігається при | 
| < 1 і розбіжний при | 
| 
1.
Необхідна ознака збіжності числового ряду. Гармонійний ряд.
Знаходження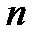 
-ої частинної суми 
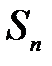і її границі для довільного ряду у багатьох випадках є непростою задачею. Тому для з'ясування збіжності ряду встановлюють спеціальні ознаки збіжності. Першою з них, як правило, є необхідна ознака збіжності.
Теорема Якщо ряд (1) збігається, то його загальний член и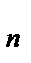 
прямує до нуля, тобто 
= 0.
□ Нехай ряд (1) збігається і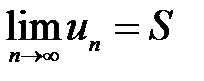 
. Тоді і 
(при 
і 
Враховуючи, що 
при 
>1, отримуємо: 
■
Наслідок 1. (достатня умова розбіжності ряду). Якщо 
0 або ця границя не існує, то ряд розбіжний.
□ Дійсно, якби ряд сходився, то (за теоремою)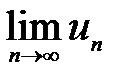 
=0. Але це суперечить умові. Значить, ряд розбіжний. ■
Теорема 1. дає необхідну умову збіжності ряду, але не достатню: з умови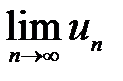 
=0 не випливає, що ряд збігається. Це означає, що існують ряди, що розбіжні, для яких, 
= 0.
Для прикладу розглянемо так званий гармонійний ряд
(7)
Очевидно, що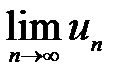 
=0. Проте ряд (7) розбіжний. Покажемо це.
Як відомо, 
Звідси випливає, що при будь-якому 
має місце нерівність 
Логарифмуючи цю нерівність на основі 
, отримаємо: 
тобто 
Підставляючи в отриману нерівність по черзі 
отримаємо:
Склавши поважно цю рівність, отримаємо 
Оскільки 
отримуємо 
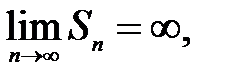тобто гармонійний ряд (7) розбіжний.
В якості другого прикладу можна взяти ряд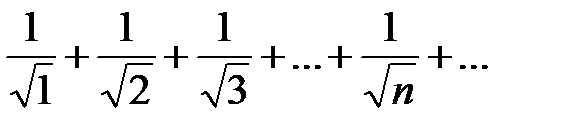 
Тут 
= 
Проте цей ряд розбіжний.
Дійсно, 
тобто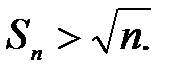 
Отже, 
при 
, ряд розбіжний.
Достатні ознаки збіжності знакосталих рядів. Необхідна ознака збіжності не дає, взагалі кажучи, можливості говорити про те, чи збігається даний ряд чи ні. Збіжність і розбіжність ряду у багатьох випадках можна встановити за допомогою так званих достатніх ознак.
Розглянемо деякі з них для знакосталих рядів, тобто рядів з від’ємними членами (знаконегативний ряд переходить знакосталий шляхом множення його на (-1), що, як відомо, не впливає на збіжність ряду).
Ознаки порівняння рядів.
Збіжність або розбіжність знакосталих ряду часто встановлюється шляхом порівняння його з іншим («еталонним») рядом, про який відомо, збігається він чи ні. В основі такого порівняння лежать наступні теореми.
Теорема Нехай дано два знакосталі ряди
(2.1) 
(2.2)
Якщо для всіх 
виконується нерівність
(2.3)
то із збіжності ряду (2.2) виходить збіжність ряду (2.1), з розбіжності ряду (2.1) виходить розбіжність ряду (2.2).
□ Позначимо 
-і частинні суми рядів (2.1) і (2.2) відповідно через 
і 
. З нерівності (2.3) виходить, що
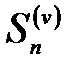(2.4)
Нехай ряд (2.2) збігається і його сума дорівнює 
. Тоді 
Члени ряду (2.2) додатні, тому 
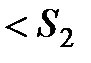і, отже, з урахуванням нерівності (2.4), 
Таким чином, послідовність 
монотонно зростає (
) і обмежена зверху числом 
За ознакою існування границі послідовно 
має границю 
тобто ряд (2.1) збігається.
Нехай тепер ряд (2.1) розбіжний. Оскільки члени ряду від’ємні, в цьому випадку маємо 
Тоді, з врахуванням нерівності (2.4), отримуємо 
тобто ряд (2.4) розбіжний. ■
Зауваження. Теорема 2.1 справедлива і у тому випадку, коли нерівність (2.3) виконується не для всіх членів рядів (2.1) і (2.2), а починаючи з деякого номера 
. Це випливає з властивості 3 числових рядів.
Теорема (гранична ознака порівняння). Нехай дано два знакосталі ряди (2.1) і (2.2). Якщо існує кінцева, відмінний від 0, границя 
то ряди (2.1) і (2.2) збігаються або розбіжні одночасно.
□ За визначенням границі послідовності для всіх , крім, можливо, кінцевого числа їх, для будь-якого 
> 0 виконується нерівність 
, або 
(2.5)
Якщо ряд (2.1) збігається, то з лівої нерівності (2.5) і теореми 14.2.1, випливає, що ряд 
також збігається. Але тоді, згідно властивості 1 числових рядів, ряд (2.2) збігається.
Якщо ряд (2.1) розбіжний, то з правої нерівності (2.5), теореми 2.1, властивості 1 випливає, що і ряд (2.2) розбіжний.
Аналогічно, якщо ряд (2.2) збігається (розбіжний), то рядом, що збігається (розбіжний) буде і ряд (2.1). ■
Ознака Даламбера. На відміну від ознак порівняння, де все залежить від здогадки і запасу відомих рядів, що збігаються і розбіжні, ознака Даламбера (1717-1783, французький математик) дозволяє часто вирішити питання про збіжність ряду, виконавши лише деякі операції над самим рядом.
Теорема 2.3. Нехай дано ряд (1) з додатніми членами і існує кінцева або нескінченна границя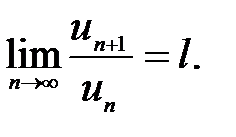 
Тоді ряд збігається при 
<1 і розбіжний при 
> 1.
□ Оскільки 
, то за означенням границі для будь-якого 
>0 знайдеться натуральне число N таке, що при п > N виконується нерівність
або 
. (2.6)
Нехай 
< 1. Можна підібрати 
так, що число 
< 1. Позначимо 
+ = 
, 
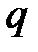<1. Тоді з правої частини нерівності (2.6) отримуємо 
або и 
< 
и 
, п>N. Через властивість 3 числових рядів можна вважати, що и 
< и 
для всіх =1,2,3... Даючи номеру 
ці значення, одержимо серію нерівностей:
тобто члени ряду 
менше відповідних членів ряду 
, який збігається як ряд геометричної прогресії із знаменником 0< 
<1. Але тоді, на підставі ознаки порівняння, збігається ряд 
, отже, збігається і початковий ряд (1).
Нехай 
>1. В цьому випадку 
. Звідси випливає, що, починаючи з деякого номера N, виконується нерівність 
>1, або 
тобто члени ряду зростають із збільшенням номера . Тому 
. На основі наслідку з необхідної ознаки ряд (1) розбіжний. ■
Зауваження.
1. Якщо 
, то ряд (1) може бути як, тим що збігається, так і тим, що розбіжний.
2. Ознаку Даламбера доцільно застосовувати, коли загальний член ряду містить вираз 
або 
Радикальна ознака Коші. Іноді зручно користуватися радикальною ознакою Коші для дослідження збіжності знакосталого ряду. Ця ознака багато в чому схожа з ознакою Даламбера, про що говорять його формулювання і доведення.
