Комплексные числа и действия над ними, их геометрическое толкование.
Функции комплексного переменного. Предел и непрерывность функции комплексного переменного.
Дифференцирование и интегрирование ФКП.
Аналитические ФКП и их связь с гармоническими функциями.
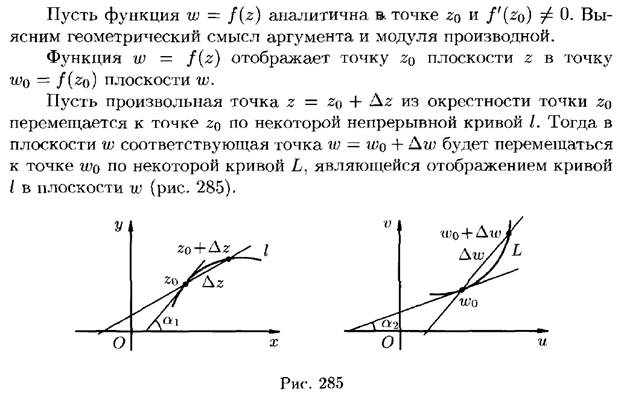
Теорема Коши.
Интегральная формула Коши.
Интеграл типа Коши.
Степенные ряды в комплексной области.
Ряд Тейлора.
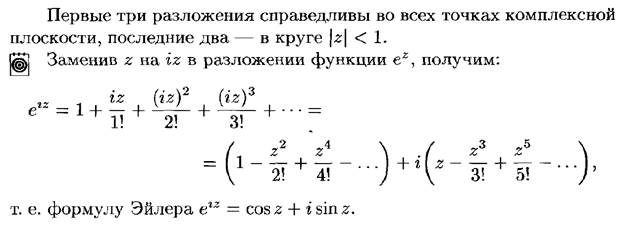
Ряд Лорана.
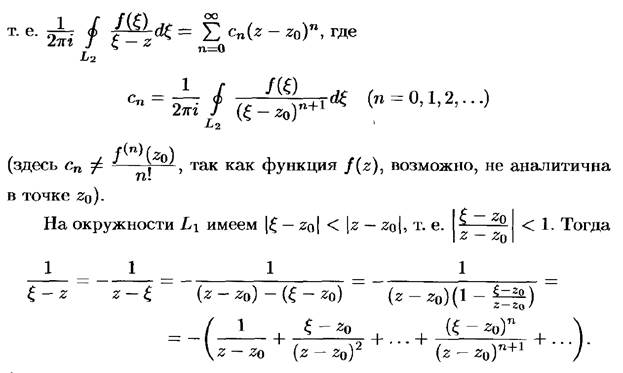
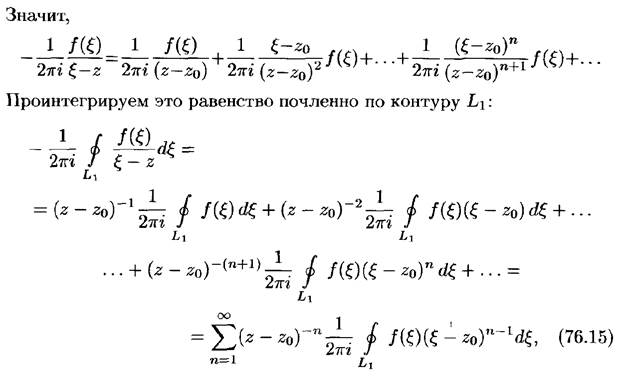
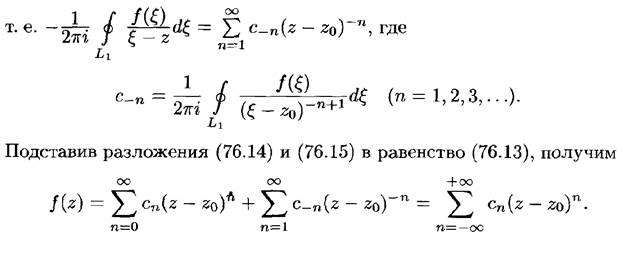
Особые точки и их классификация.
Вычеты и их вычисление. Теорема Коши о вычетах.
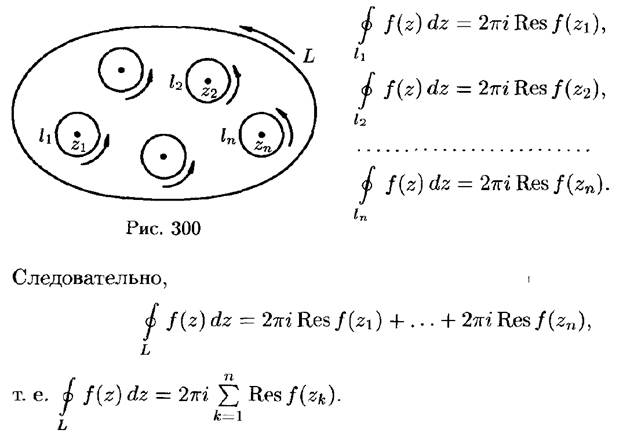
Применение вычетов и вычислений интегралов.
Преобразование Лапласа и его свойства.
Теоремы единственности, подобия, линейности, смещения изображения.
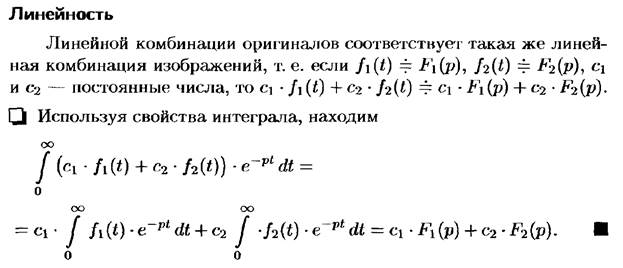
Теоремы дифференцируемости и интегрируемости изображения и оригинала.
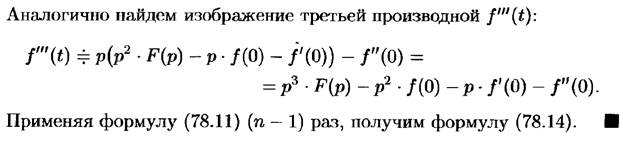
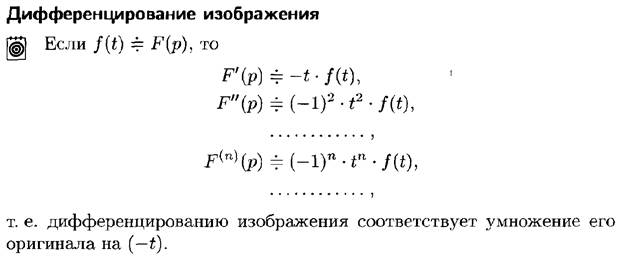
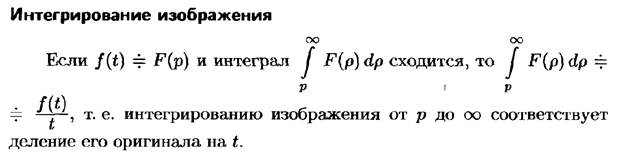
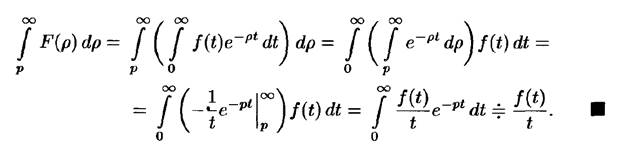
Решение обыкновенных дифференциальных уравнений и систем операционным методом.
Элементы комбинаторики. Схема случаев.
Классическое определение вероятности.
Геометрическое определение вероятности.
Условная вероятность. Теоремы сложения и умножения вероятностей.
Формулы полной вероятности и Байса.
Повторные испытания. Формула Бернулли и ее приближения (формула Пуассона, локальная и интегральная теоремы Муавра-Лапласа).
Испытания наз. независимыми, если вероятность результата каждого события А в каждом испытании не зависит от того, какие результаты имели предыдущие испытания, то такие испытания наз. независимыми относительно соб. А.
Если делается n независимых испытаний в одинаковых условиях, причем в каждом из них событие А появляется с вероятностью р, то вероятность появления в этих испытаниях события А равно m раз и находится по формуле Бернулли.
Формула Бернулли. Если вероятность р наступление события А в каждом испытании постоянна, то вероятность того, что в n независимых испытаниях событие А наступит ровно m раз, вычисл. по формуле
,
Где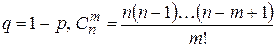 
Если число испытаний велико, а вероятность успеха мала, то вероятность m успехов в n испытаниях рассчитывается по формуле Пуассона.
Th. Пуассона. Если вероятность наступления события А в каждом испытании постоянна, но мала, а число n достаточно большое, но число 
небольшое, то вероятность того, что в этих испытаниях событие А наступит m раз вычисляется по формуле Пуассона:
.
Условие применения формулы Пуассона: 
При больших n пользуются локальной теоремой Муавра- Лапласа, которая дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события m раз из n испытаний, если число испытаний достаточно велико.
Th. Если вероятность Р появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Pn(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции:
Где 
- называется функцией Лапласа.
Для вычисления функции 
имеются таблицы, при чом для 
и владеет такими свойствами:
1. 
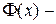непарная, т.е. 
2. 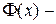монотонно возрастающая, т.е. при 
3. граница функции при 
равна единице 
4. для всех значений 
строго больше 4 можно считать, что 
