По требованию курсового проекта необходимые электрические и геометрические параметры антенны в КВ диапазоне будут рассчитаны исходя из заданной диаграммы направленности, спроектированной в программе MMANA - GAL basic.
ДН данной антенны рассчитывается по формуле:
Полагая для приближённого анализа, что амплитуда бегущей волны вдоль провода спирали не меняется, ДН спиральной антенны можно представить произведением ДН одиночного витка на множитель решётки.
В области малых значений угла θ выражение для ДН одиночного витка с бегущей волной можно приближённо записать в виде:
F1θ(θ) ≈ cos(θ); (1)
F1φ(θ) ≈ cos(θ). (2)
где F1θ(θ) — нормированная ДН меридиональной составляющей поля;
F1φ(θ) — нормированная ДН азимутальной составляющей поля.
Из формул (1), (2) видно, что одиночный виток характеризуется слабой направленностью и концентрация излучаемой энергии вдоль оси спирали получается, очевидно, за счёт близкого к синфазному сложения полей витков в этом направлении.
Поэтому можно считать, что ДН спирали определяется множителем решётки:
(3)
где n — число витков;
S — расстояние между соседними витками;
θ — угол, отсчитываемый от оси спирали;
ψ — сдвиг по фазе между точками в соседних витках.
В режиме осевого излучения сложение полей отдельных витков в направлении оси спирали должно быть близким к синфазному. Для того чтобы это могло иметь место, ток в каждом последующем витке должен отставать по фазе от тока в предыдущем на угол:
Ψ = (2∙π/λ)∙S + 2∙π (4).
Сдвиг по фазе между токами в соседних витках можно представить формулой:
Ψ = (2∙π/λсп)∙L, (5)
где λсп — длина волны в проводе спирали.
Приравнивая выражения (4) и (5), получим условие синфазного сложения полей вдоль оси спирали в виде:
S/λ + 1 = L/λсп, (6)
откуда
L = (S+λ)/ξ, (7)
где ξ = λ/λсп — коэффициент укорочения волны.
Так как в цилиндрических спиральных антеннах ξ имеет значение от 1 до 1,4, то длина витка L в режиме осевого излучения должна быть примерно равной длине волны λ.
(8).
Тогда ДН спиральной антенны, равная произведению ДН одиночного витка на множитель решётки определится выражением:
С учётом (5) и (7) формулу (3) можно привести к виду:
Рисунок 4 – ДН спиральной антенны при частоте 30 МГц
Рисунок 4.1 – 3D модель ДН спиральной антенны при частоте 30 МГц
Рассчитаем шаг спирали:
Ширина диаграммы направленности:
Откуда 
,
Длину антенны вычислим по формуле:
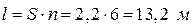
Длину витка спирали, при которой излучение максимально вдоль оси нужно выбрать из интервала 
, 
Радиус спирали:
Диаметр проводника антенны:
Диаметр экрана:
Угол подъема спирали:
Коэффициент направленного действия:
Входное сопротивление антенны:
Чтобы наглядно продемонстрировать излучение антенны в диапазоне УКВ, воспользуюсь программой проектирования, где эта же антенна будет излучать на частоте 2400 МГц.
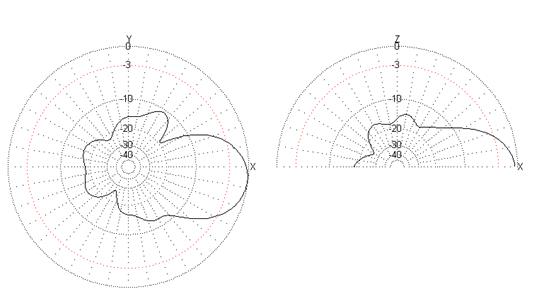
Рисунок 5 – ДН антенны цилиндрической спиральной антенны в УКВ диапазоне
Рисунок 6.1 – 3D – модель излучения цилиндрической спиральной антенны в УКВ диапазоне
Рисунок 6.2 – 3D – модель излучения цилиндрической спиральной антенны
в УКВ диапазоне
Расчет питающей линии
Подключение антенны к входу приемника или выходу передатчика осуществляется с помощью соединительных линий, которые называютсяся фидерами(от английского to feed-питать). В зависимости от назначения антенны устанавливаются либо на антенном поле на большом расстоянии от технического здания, где расположена передающая или приемная аппаратура, либо на высоких опорах(мачтах или башнях). Исключение составляют приемно-передающие системы подвижной связи, где антенны и приемно-передающая аппаратура часто составляют единый интегральный модуль.
На более высоких частотах (метровые и дециметровые волны) симметричные фидеры начинают излучать или принимать радиоволны подобно антеннам. Это явление называется антенным эффектом. Антенный эффект приводит к дополнительным потерям энергии на излучение и приводит к искажениям диаграмм направленностей приемных и передающих антенн.
Поэтому в диапазоне метровых и дециметровых волн применяют в качестве фидеров коаксиальные линии. Коаксиальные линии со сплошным заполнением диэлектриком называются коаксиальными кабелями.
В качестве фидеров передающих KB антенн наиболее часто используются двух- и четырехпроводные воздушные симметричные линии (рис. 8), также четырехпроводные перекрещенные фидеры (рис. 9), состоящие из соединенных перемычками крест-накрест проводов. Эти фидеры обычно выполняют из биметаллических (стальной провод, покрытый медной оболочкой) проводов диаметром 3... 6 мм. Расстояние между проводами составляет 225... 450 мм. Двухпроводные фидеры (W = 600 Ом) могут пропускать мощность до 50кВт, четырехпроводные (W = 300 Ом) — до 100 кВт. При больших уровнях мощности провода фидера выполняются в виде многопроволочных цилиндров (рис. 9). Волновое сопротивление двухпроводного (однопроволочного) фидера при 
(что обычно имеет место) равно:
W = 276 lg(D/a).
Четырехпроводный однопроволочный симметричный неперекрещенный фидер имеет:
Перекрещенный —
,
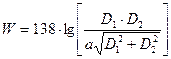Для питания передающих антенн используют также несимметричные концентрические и несимметричные плоские. В случае концентрического фидера многопроволочным может быть выполнен только внешний провод или оба — внешний и внутренний провода. Симметричные фидеры крепят на деревянных, асбоцементных или железобетонных опорах. Последние используются для подвески тяжелых фидеров W= 120 Ом. К опорам фидеры крепят с помощью специальных изоляторов.
Основными параметрами, которыми оценивается качество передающего фидера, являются пропускная мощность и КПД. Максимальная мощность, пропускаемая фидером, определяется электрической прочностью изоляторов и воздуха, окружающего фидер. Если напряженность поля превосходит некоторое определенное значение, то начинается ионизация воздуха, что может привести к его пробою.Начальная напряженность поля равна примерно 30 кВ/см. Обычно принимается, допустимая амплитуда напряженности поля Е доп примерно равна 6... 7 кВ/см. Максимальная напряженность поля возникает у поверхности провода. Ее ток распределен равномерно по периметру проводника, то I= 2p На (Н — напряженность магнитного поля). Так как вдоль воздушной линии распространяются Т-волны, то E=WCH, где W с=120 pОм, и, следовательно, Етax = 120p I /2p a. Поскольку I=U/W, где U — напряжение между проводами линии, то Emax = 60 U/(aW). В многопроводной линии ток, приходящийся на один провод, уменьшается в п раз (п —число пар проводов), и в данном случае:
.
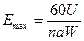Амплитуда напряжения в пучности связана с мощностью, передаваемой по линии, соотношением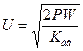 
. После подстановки этого выражения в получаем:
.
Здесь Етах — амплитуда напряженности электрического поля у поверхности проводника в пучности напряжения. Мощность, которую можно передать по воздушной линии без опасности факельного истечения, причем заменяют Етах на Едоп :
Если провода фидера выполнены из многопроволочных цилиндров, то
.
Коэффициенты x1 и x2, учитывающие неравномерность распределения по проводам цилиндра, показывают, во сколько раз ток в проволоке с максимальным значением тока превышает среднее значение I/п. Коэффициент x2 учитывает неравномерность распределения тока по периметру одной проволоки. Коэффициент x1 зависит в основном от волнового сопротивления и типа фидера. Коэффициент x2 можно оценить по формуле
x2 = 1 + (n — 1) a / R, где а — радиус провода, R — радиус цилиндра; n — число проволок в цилиндре.
Для увеличения электрической прочности фидера надо стремиться к тому, чтобы коэффициент x1 был близок к единице. Этого можно добиться неравномерным размещением проволок в цилиндре. Коэффициент полезного действия фидера равен отношению активной мощности, выделяемой в нагрузке на конце фидера (Р н), к полной активной мощности, подведенной к началу линии Р 0.
Если отражение от нагрузки отсутствует, то КПД можно найти по формуле:
,
где L — длина фидера; aф = R 1 /2W —коэффициент затухания; R 1— сопротивление фидера на единицу длины.
Расчет фидера:
Зададим некоторые параметры для расчета питающей линии:
D=20 см расстояние между проводниками
а=3мм радиус проводника
U=110В напряжение в фидере
n= 2 количество пар проводников
P=5 кВт
Едоп=6 В/см
R=7мм радиус цилиндра
R1=75 Ом сопротивление фидера на единицу длины
L=3м длина питающей линии
1. Рассчитаем волновое сопротивление фидера:
2. Рассчитаем максимальную напряженность электрического поля фидера:
3. Рассчитаем значение дополнительной мощности:
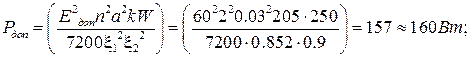
Где к-коэффициент, ξ1ξ2- коэффицтенты, учитывающие неравномерность распределения по проводам цилиндра, показывают, во сколько раз ток в проволоке с максимальным значением тока превышает среднее значение I/п
4. Рассчитаем КПД фидера:
КПД в общем случае:
Загоризонтальная передача
В свободном пространстве (ero = l; mro = l; sо = 0) амплитуда напряженности электрического поля в точке наблюдения (точке приема) равна:
,
где 
— мощность, подводимая к передающей антенне; G 1 — коэффициент усиления передающей антенны относительно изотропного излучателя; r— расстояние от точки передачи до точки приема.
Произведение 
= P 1экв называют эквивалентной мощностью излучения, которую надо подвести к ненаправленной антенне, чтобы получить в точке приема такую же напряженность поля, как от направленной антенны с коэффициентом усиления G 1, к которой подведена мощность . Из (15.1) следует, что даже в свободном пространстве, среде без потерь, напряженность поля в точке приема убывает обратно пропорционально первой степени расстояния, что обусловлено уменьшением плотности мощности (среднего за период колебаний значения вектора Пойнтинга) при удалении от источника. Во многих случаях, например при расчете радиолиний в диапазонах коротких (KB), средних (СВ) и длинных (ДВ) волн, пользуются не амплитудным, а действующим значением напряженности поля, которое в условиях свободного пространства:
.
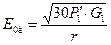При расчете и проектировании радиолиний, особенно в диапазонах сантиметровых и дециметровых волн, необходимо знать мощность сигнала на входе приемника. Эта мощность определяется различно для радиолиний двух типов. На радиолинии I типа передача информации ведется непосредственно из пункта передачи в пункт приема. На радиолиниях II типа принимаются сигналы, испытавшие пассивную ретрансляцию на пути от передатчика к приемнику. На этих линиях непосредственная передача энергии волны от источника до точки приема по каким-либо причинам невозможна (например, этот путь перекрыт препятствием). На наземных радиолиниях с пассивной ретрансляцией на пути распространения имеется специальное антенное устройство, которое облучается первичным полем и переизлучает его в виде вторичного поля, предназначенного для приема. По такому же принципу работают системы пассивной радиолокации, где первичное поле облучает обнаруживаемую цель, а поле, переизлученное целью, принимается локатором.
На любой радиолинии мощность на входе приемника Р 2связана с плотностью потока мощности в месте приема П2 соотношением:
Р2 = Л2S д × h2,
где h2 — КПД фидера приемной антенны; 
— действующая площадь приемной антенны. На радиолинии I типа в условиях свободного пространства плотность потока мощности в месте приема:
,
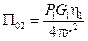На радиолинии II типа значение П02 зависит от тех же параметров, что и на линии I типа, и, кроме того, от переизлучающих свойств ретранслятора. Если какое-либо тело облучается полем, то его способность переизлучать это поле оценивается эффективной площадью рассеяния sэф (ЭПР). Величина ЭПР зависит от формы, размеров, электрических свойств материала, из которого выполнен переизлучатель, а также от его ориентации относительно направления распространения первичного поля и направления на прием.
Если около переизлучающего тела плотность потока мощности первичного поля 
, то переизлученная мощность:
P 0П = П 0П × sэф,
а плотность потока мощности вторичного поля вблизи приемной антенны в условиях свободного пространства:
.
.
В тех случаях, когда r 1 = r2 = r,
.
Из формул видно, что в свободном пространстве при отсутствии пассивного ретранслятора на линии мощность на входе приемника уменьшается обратно пропорционально квадрату расстояния, а при работе с ретранслятором — обратно пропорционально четвертой степени. Такое быстрое убывание поля на линиях II типа объясняется тем, что поле дважды испытывает расходимость: первичное поле — на пути от источника (передающей антенны) до ретранслятора и вторичное поле — на пути от источника (ретранслятора) до пункта приема.
При проектировании систем удобно иметь сведения о потерях при передаче электромагнитной энергии. Потерями передачи L называют отношение мощности , подводимой к передающей антенне, к мощности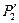 
на входе приемной антенны:
,
где Р 1— мощность на выходе передатчика; Р 2— мощность на входе приемника.
Полные потери передачи обычно выражают через L 0. Так, можно записать:
В случае реальных сред, отличных по своим свойствам от свободного пространства, вводят так называемый множитель ослабления:
,
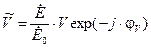где V — модуль множителя ослабления, который оценивает дополнительное ослабление амплитуды напряженности поля по сравнению с ее ослаблением в условиях свободного пространства; j V — фаза множителя ослабления, которая оценивает дополнительное изменение фазы волны. Из следует, что
.
Потери передачи на радиолиниях I типа
,
а на радиолиниях II типа (при r 1 = r 2 = r)
Вывод
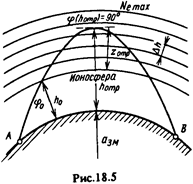
В курсовом проекте были рассчитаны геометрические и электрические параметры цилиндрической спиральной антенны по заданному графику диаграммы направленности. Расчёт антенны произведен для КВ диапазона в передающем режиме для загоризонтальной передачи. На практике спиральные антенны работают в УКВ диапазоне, в этом случае загоризонтальная передача осуществляется с помощью ретрансляторов, стоящих на расстоянии 50 километров друг от друга, так как ультра короткие волны распространяются в пределах прямой видимости. Для передачи КВ волн с помощью таких антенн необходимо использовать отражение от ионосферы. Массо-габаритные соотношения спиральных антенн КВ диапазона очень велики и осуществить использование таких антенн не представляется целесообразным.
Для наглядности излучения антенны в пространстве, была смоделирована трёхмерная модель антенны в идеальных условиях (без учёта земли). Объёмная диаграмма излучения повторяет форму тороида, что подтверждает теоретический материал, представленный в одном из пунктов. Для моделирования использовалась программа MMANA – GAL basic.
Список литературы:
1. Под редакцией Г.З. Айзенберга «Антенны УКВ», Ч. 2, М., «Связь», 1977.
2. Д.М. Сазонов «Антенны»
3. В.В. Никольский «Антенны и устройства, работающие в СВЧ диапазоне»
4. А.С. Лавров Г.Б. Резников «Антенно-Фидерные Устройства» Советское радио Москва 1974
5. Г.Б. Белоцерковский «Основы радиотехники и антенны» Радио и Связь 1974
6. Программное обеспечение MMANA – GAL basic V 3.0.0.25, Makoto Mori
