Тақырып. Кодтар, антикодтар. Хемминг коды.

Жоспар: Кодтар, антикодтар. Хемминг кодымен таныстыру.

Кілттік сөздер: антикод, қайтымды кодтар

Иллюстрациялық материал: слайд

Информатиканың бастапқы түсініктерін қарастырғанда біз дискретті ақпаратты анықтау үшін кейбір алфавиттерді қолданатынын білдік. Бірақта ақпарат пен алфавит арасында біртектілік сәйкестік жоқ. Басқа сөзбен айтқанда, бір ақпарат әр түрлі алфавит арқылы көрсетілуі мүмкін. Мұндай мүмкіндіктің арқасында бір алфавиттен екіншісіне өту мәселесі туындайды, бірақта мұндай алмастыру ақпаратты жоғалтуға алып келмеуі тиіс. Алмастыруға дейінгі ақпаратты– алғашқы; ал соңында көрсетілетін, яғни кодталған ақпаратты- екінші деп атауға келісейік.

Анықтамалар тізбегін еңгізейік:

Код – (1) сәйкес белгілерді бейнелейтін немесе олардың бір алфавиттің белгілермен сәйкес келуін зерттейтін ереже болып табылады; - (2) белгілерді көрсету үшін немесе олардың алғашқы алфавитпен сәйкес келуі үшін қолданатын екінші алфавиттің белгілері.

Кодтау – алғашқы алфавиттен кодтар тізбегімен көрсетілген ақпараттың алмасуы.

Декодтау – қайтымды кодтау операциясы, яғни алынған кодтар тізбегінен ақпаратты алғашқы алфавитке келтіру.

Кодтау және декодтау операциясын қайтымды деп атайды, егер олардың қолдану тізбегі ақпаратты жоғалтуынсыз бастапқы қалпына келуін қамтамасыз ететін болса.

Қайтымды кодтаудың мысалы болып телеграфтық кодтауындағы белгілер табылады. Қайтымды емес кодтаудың мысалы ретінде бір тілден екінші тілге аудару және керісінше аударманы алуымызға болады.

Осылайша, кодтау ақпарат беруді және сатауды қамтамасыз етеді. Ертеректе айтылып кеткендей, ақпаратты сақтау оның таратушыларына байланысты, ал ақпарат беру – уақыт ағымындағы күйінің аласуына байланысты. Бұл күйлерді немесе дыбыстарды элементарлы дыбыстар деп атаймыз.

Келесі қадамда кодтау есебінің математикалық қойылымын қарастырамыз.

 

Дәріс

Тақырып. Сызықтық (топтық кодтар). Циклдық кодтар. Синдроп бойынша декодтау.

Жоспар: Сызықтық кодтар. Циклдық кодтар. Синдроп бойынша декодтау.

Кілттік сөздер: цикл, синдроп

Иллюстрациялық материал: слайд

Сызықтық (топтық кодтар). Циклдық кодтар. Синдроп бойынша декодтау.

Теориялық информатика. Шеннон теориясында ақпаратты кодтау. Компьютерде санды қамтамасыздандыру. Компьютермен әр түрлі есептеу және есептік информация арқылы есеп шығарғанда немесе компьютерлік графикада қолданады. Осыдан таңдау жүргіземіз, компьютердегі оптималдық санды нақты 8- битті (байттық) бүтін санға қолданылатын кодтау. Бірақ, бұндай кодтау оптималды болмайды. Оны мына мысалдан көруге болады: берілген екі мәнді 13- саны 8- битті кодтау бөлек цифрларды ASCII кодында оның әдісі былай болып көрінеді: 00110001001100011 код 16- бит ұзындық болды. Егер ол екілік каскада бойынша берілсе,(мысалы, таңдаулы каскад алсақ «Угадай-ка- 16» бұдан бері жазылды) онда төрт битті тізімді аламыз 1101. Маңызды әр түрлі түрмен көрсетпей-ақ берілгенді (әріп немесе сан) көрсету. Онымен операцияларды жасау. Әріптердің орнын бірдей қалдыру, санды өзгерту. Мысалы, басқа санның көмегімен түбір табу. Компьютердегі формалармен салыстырғанда мектеп кезінен келе жатқан екі маңызды түбір бар «Біріншіден сан екілік санау жүйесі бойынша жазылады(бірінші ондықтан қарағанда). Екіншіден санның жазылғанда аяқты разрядтардан басталады(арифметикада бұндай тәсіл мүмкін емес)»

 

Дәріс

Тақырып. Симметриялық емес қателіктерді түзететін квадрат.

Жоспар: квадрат көмегімен симметриялық емес қателіктерді түзетіп үйрету.

Кілттік сөздер: симметрия

Иллюстрациялық материал: слайд

Симметриялық емес қателіктерді түзететін квадрат

Хемминг бірінші болып «қателерді түзейтін кодтарды» (Error-Correcting Code, ECC) ұсынғандығы анық екенін білеміз. Бұл кодтардың қазіргі заманғы модификациялары барлық ақпараттарды сақтау жүйелерінде және жад пен процессор арасындағы алмасулар үшін қолданатыны белгілі. Олардың бір нұсқасы Рид-Соломонның коды компакт-дискілерде қолдланылады. Хэмминг тәсілі бойынша жасалынған көптеген кодтар нұсқалары бар, олар кодтау алгоритмдері бойынша және тексеретін биттер саны бойынша айырмашылықтары бар. Мұндай кодтарға планетааралық станциялармен космостық байланыс жасау үшін ерекше көңіл беріле бастады, мысалы, Рид-Мюллердің кодтарын 7 ақпараттық битке 32 тексеруші бит немесе 6 ақпараттық битқа – 26 тексеруші биттар келетін болды. Хемминг өзінің мақаласын 1950 жылы жарыққа шығарды, бірақта ішкі жазбаларда кодтау теориясы 1947 жылмен белгіленген. Сондықтанда кейбіреулер кодтау теориясының атасы ретінде Шеннонды емес, Хеммингті атау керек деп ойлайды. Бірақта, техника тарихында алғашқыны іздеу пайдасыз нәрсе.

ECC жаңа кодтардың бірі ретінде LDPC (Low-Density Parity-check Code) кодын айтуымызға болады. Негізінде олар отыз жыл бұрын танымал блған, бірақта қазіргі уақытта оларға ерекше көңіл бөлінуде. LDPC коды 100-пайыздық анықтылығы бомағанмен, ол қатенің мүмкіндігін керекті нәтижеге дейін жеткізуімізге мүмкіндік береді және сонымен қатар каналдың жіберу мүмкіндігі максимальді толық түрде қолданылады. Оларға «турбокодтар» (Turbo Code) өте жақын келеді, олар алыс космостағы объектілермен жұмыс жасағанда өте қолайлы.

 

Дәріс

Тақырып. Байттық кодтардың халықаралық жүйелері. Рида – Маллер кодтары.

Жоспар: Рида – Маллер кодтарымен таныстыру.

Кілттік сөздер: алфавит, халықаралық жүйе

Иллюстрациялық материал: интернет сайты

Рида – Маллер кодтары

Әрбір белгіге ақпараттың орта мәніне тең келетін N белгі A алғашқы алфавитінде бар болсын және олардың бар болу мүмкіндігі анықталған болсын I₁^(A) (төменгі индекс бірінші қозғалысты қарастыратынжағдайларды көрсетеді, ал жоғарғы индекс жақшаның ішінде алфавитті көрсетеді). I₁^(A) ақпараттық орта сиымдылығына сәйкес келетін М белгі В екенін алфавитінде бар болсын, алфавитте көрсетілетін бастапқы мәліметтерде n белгілер, ал кодтталған мәліметтерде – m белгілер бар болсын. Егер бастапқы мәліметте I^(A) ақпарат бар болса, онда кодтталғанда – I^(B) болсын. Сонда кодттаудың қайтымы шарты төмендегідей жазылады:

I^(A) 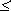I^(B),

Мұның мәні қайтымды кодттаудың операциясы мәліметтердегі ақпарат санын көбейте алады, бірақ оны көшіре алмайтынын көрсетеді. Бірақ бұл теңсіздіктегі әрбір шартты сыйымдылық белгісімен алмастыра алады, яғни алғашқы алфавиттің белгісін

m/n, қатынынасы кодттау үшін қлданылатын екінші алфавиттің белгілерінің орта мәнін сипаттайды және оны код ұзындығы немесе код тізбегінің ұзындығы деп атайды және K^(B) деп белгілейміз(жоғарғы индекс алфавиттің кодттарын көрсетеді).

Жеке жағдайда, I₁^(B)=log₂M, Хартли формуласына сәйкес екінші алфавиттің керек белгілерінің пайда болуы мүмкін болғанда, сонда

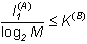(1)

Шығады.

Тілдің артықшылығын сипаттайтын R биіктігінің аналогиясы бойынша кодттың артықшылық қатынасын (Q) енгізуімізге болады:

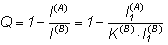(2)

Көрсетілген шарт бойынша кодттау операциясы бастапқы мәліметті қанша есеге дейін ұзартқандығын көре аламыз Q кіші болған жағдайда кодттың тиімді екенін көрдік.

Дәріс

Тақырып. Мебиус функциясы және синхромизацияланатын кодтар.

Жоспар: Синхромизацияланатын кодтармен таныстыру.

Кілттік сөздер: мебиус функциясы

Иллюстрациялық материал: слайд

Мебиус функциясы және синхромизацияланатын кодтар

Мәліметтерді кодтаудың қажеттілігімен алғашқы рет жүз елу жыл бұрын тап болды. Каналдар өте қымбат және сенімсіз болғандықтан телеграммаларды жіберудің өте тиімді жолдары қарастырылды.1845 жылы пайдалануға арнайы кодтау кітаптары шықты; олардың көмегімен телеграфистер қолмен мәліметтердегі ұзақ сөйлемдерді қысқа кодтармен алмастырды. Сол кездері мәліметтердің жіберілуінің дұрыстығын тексеру үшін жұптық бақылау әдісі қолданылды, бұл әдісті перфокарталардың дұрыстығын тексеру үшін компьютердің бірінші және екінші буындарында да қолданылды. Ол үшін ең соңғы мәліметтер колодасына арнайы дайындалған бақылау сомасы бар картаны салған. Егер енгізу құрылғысы сенімсіз болса (немесе колода тым ұзын болған жағдайда), онда қате тууы мүмкін. Оны жөндеу үшін картадағы сомамен сәйкес келмегенше процедураны қайталай беретін. Бұл сұлбаның ыңғайсыз болғанымен қатар, ол екі есе қателер жіберетін.

Мебиус функциясы байланыс каналдарының дамуымен қатар бақылаудың өте тиімді механизмі керек болды.

Бұл мәселенің теориялық шешімін алғашқы болып ақпараттың статистикалық теориясынының негізін қалаушы Клод Шеннон ұсынды. Шеннон өз заманының жұлдызы болды,ол АҚШ-тың академиялық элитасынынң мүшесі болған. Ванневар Буштың аспиранты болып, ол 1940 жылы жасы 30 жетпеген оқымыстыларға берілетін Нобель атындағы сыйлыққа ие болды (Нобель премиясымен шатастырмаңыздар). Bell Labs жұмыс істеп жүріп Шеннон «Мәліметтерді жіберудің математикалық теориясы» (1948) атты жұмыс жазды, ол жұмыста Шеннон каналдың жіберу мүмкіндігі мәліметтердің энтропия бастауынан жоғары болса, онда мәліметтерді ешқандай ақаусыз жіберілетіндей етіп кодтап қоюға болатынын дәлелдеді.Бұл түйіндеме Шеннонның көптеген дәлелдеген теоремалардың біреуінде бар. Сонымен қатар, ол каналда шудың бар болуына қарамастан мәліметтің жіберілу мүмкіндігінің теориялы түрде дәлелдеп берді.Шеннонның Мичиган штатында өзінің туып өскен қаласында орнатылған ескерткішінде ойып жазылған формуланы C = W log ((P+N)/N) Альберт Эйнштейннің E = mc² формуласының мәнімен салыстырады.

Шеннонның еңбектері ақпараттар теория облысындағы ары қарай зерттеулерінде өз ықпалын тигізді, бірақта оларда инженерлік практикалық қосымшасы бар болмады. Теориядан практикаға алмасу Ричарда Хэммингтің жұмысынан байланысты болды. Ол Шеннонның Bell Labs бойынша әріптесі болды және кодтар класын ашқандығы үшін әйгілі болды, оларды «Хэмминг коды» деп атады. Өзінің жаңалығын Хемминг 40 жылдардың ортасында Bell Model V есептеуіш машинасының перфокарталармен жұмыс жасау қолайсыздығынан ашты деген аңыз бар. Оған операторлар жоқ болғанда, яғни демалыс күндерде машинамен жұмыс жасауға мүмкіндік берді және ол өзі енгізулермен жұмыс жасады. Хемминг байланыс каналдарындағы, сонымен қатар компьютерлердегі ақпараттарды беру магистральдарында, ең бастысы жад пен процессор арасындағы қателерді түзете алатын кодты ұсынды. Хемминг коды Шеннон теоремасында көрсетілген мүмкіндіктерді практикалық түрде қалай іске асыруға болатындығын көрсетеді.

Хемминг өзінің мақаласын 1950 жылы жарыққа шығарды, бірақта ішкі жазбаларда кодтау теориясы 1947 жылмен белгіленген. Сондықтанда кейбіреулер кодтау теориясының атасы ретінде Шеннонды емес, Хеммингті атау керек деп ойлайды. Бірақта, техника тарихында алғашқыны іздеу пайдасыз нәрсе.

Хемминг бірінші болып «қателерді түзейтін кодтарды» (Error-Correcting Code, ECC) ұсынғандығы анық екенін білеміз. Бұл кодтардың қазіргі заманғы модификациялары барлық ақпараттарды сақтау жүйелерінде және жад пен процессор арасындағы алмасулар үшін қолданатыны белгілі. Олардың бір нұсқасы Рид-Соломонның коды компакт-дискілерде қолдланылады. Хэмминг тәсілі бойынша жасалынған көптеген кодтар нұсқалары бар, олар кодтау алгоритмдері бойынша және тексеретін биттер саны бойынша айырмашылықтары бар. Мұндай кодтарға планетааралық станциялармен космостық байланыс жасау үшін ерекше көңіл беріле бастады, мысалы, Рид-Мюллердің кодтарын 7 ақпараттық битке 32 тексеруші бит немесе 6 ақпараттық битқа – 26 тексеруші биттар келетін болды.

ECC жаңа кодтардың бірі ретінде LDPC (Low-Density Parity-check Code) кодын айтуымызға болады. Негізінде олар отыз жыл бұрын танымал блған, бірақта қазіргі уақытта оларға ерекше көңіл бөлінуде. LDPC коды 100-пайыздық анықтылығы бомағанмен, ол қатенің мүмкіндігін керекті нәтижеге дейін жеткізуімізге мүмкіндік береді және сонымен қатар каналдың жіберу мүмкіндігі максимальді толық түрде қолданылады. Оларға «турбокодтар» (Turbo Code) өте жақын келеді, олар алыс космостағы объектілермен жұмыс жасағанда өте қолайлы.

Бұл теореманы әркім әрқалай атайды, соның ішінде «WKS теоремасы» (аббревиатура WKS взята от Whittaker, Kotelnikov, Shannon). Кейбір бастауларда Nyquist-Shannon sampling theorem және Whittaker-Shannon sampling theorem деп те аталады, ал өзіміздің жоғарғы оқу орындарының оқулықтарында жай ғана «Котельников теоремасы» деп кездестіреміз. Шын мәнінде теореманың өзіндік тарихы бар. Оның бірінші бөлігін 1897 жылы француз математигі Эмиль Борель дәлелдеген. Ал 1915 жылы өзінің еңбегін Эдмунд Уиттекер қосты. 1920 жылы жапондық Кинносуки Огура Уиттекер зерттеулеріне өзінің жөндеулерін жариялады, ал 1928 жылы американдық Гарри Найквист цифрлардың принциптерін және аналогтық сигналдың қайтадан қалпына келуін дәлелдеді.

Дәріс

Тақырып. Латындық квадраттар және кодтар.Адамар матрицалары және кодтау.

Жоспар: Латындық квадраттар және кодтар түрін қарастыру

Кілттік сөздер: квадрат

Иллюстрациялық материал: слайд

Латындық квадраттар

Ақпаратты жіберуде кедергілер болмаған жағдайда мәліметтерді кодтаудың мынандай нұсқасын кодтайтын алфавиттің бір белгісіне сәйкес келетіні бар болуы мүмкін, код белгілерінің орташа мәні алғашқы және екінші алфавиттің ақпараттық орта мәнінің қатынасына жақын болады.

Кодтық артықшылық түсінігін пайдалана отырып бұл теорияны қысқаша былай жазуымызға болады:

Ақпарат жіберуде кедергілер болмаған жағдайда мәліметтерді кодтаудың мынандай нұсқасы бар болады: код артықшылығы әр уақытта 0-ге жақын болады.

Бұл ереже теорема болып табылғандықтан олар дәлелдеуі тиіс. Бірақ біз оны дәлелдемейміз. Бізге теорема кодтаудың оптимальді мүмкіндікті алатыны өте маңызды.

Ары қарай M = 2 жағдайымен шектейміз, яғни жолдарында кодтты көрсететін екі тип сигналдары қолданылады- бірінші іске асырылатын нұсқа ал екінші оның жоқ болуы(пауза); бар болуы және жоқ болуы; мұндай кодттауды екілік кодттау деп атайды.

Екілік алфавиттің белгілерін "0" және "1" деп белгілейміз,бірақ оларды сан ретінде емес әріп ретінде қарастыруымыз керек. Бұл кодттың қолайлылығы санда әрбір элементарлы сигнал өзінде1 бит ақпараты бар (log₂M = 1); сонда Шеннонның 1-ші теоремасын аламыз:

I₁^(A) 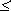K⁽²⁾

және Шеннонның бұл теоремасы келесідей сипатталады:

Ақпарат жіберуде кедергілер болиаған жағдайда екілік кодттың орташа ұзындығы алғашқы алфавиттің белгісіне келетін ақпараттың орта мәніне сәйкес келеді.

Екілік кодттау үшін формула келесідей болады:

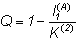
Екілік кодттауда жіберілген ақпараттың санының анықтамасы импульстар(бірлік) және паузалардың (ноль) санын есептеумен аламыз. Осы кезде мынандай проблема туады: жеке кодттардың амалдар ағымынан ажыратып алуы.

Қабылдағыш құрылғы дыбыстың ұзындығы мен жиілігін белгілейді. Элементарлы дыбыстар бірдей немесе әр-түрлі ұзындықта болуы мүмкін. Олардың кодттағы саны да бірдей немесе әр түрлі болуы мүмкін. Нәтижесінде кодттау кезінде келесі байланыс нұсқалары бар болуы мүмкін:

кесте 1. Қиылысу нұсқалары