Эллипсойд бетіндегі кез келген нүктесіндегі қисық тұрақты емес, сол себепті әр нүктеде көп шамалы жазықтықта қисықтар радиусын алуға болады. Эллипсоидтың кез келген нүктесінде екі өзара перпендикуляр нүкте болады, олар үшін қисықтар радиусы экстималды болып саналады. Мұндай бағыттар үшін меридиан бағыты қисық радиусының минималымен және бірінші ввертикалдың бағыты қисық радиусының максималына тең болады. Қисықтың барлық жеке радиустары осы экстремал радиустар арасында орналасқан. Меридиандық қилыстың қисық радиусы мен бірінші вертикалдың қилысы қисықтың басты радиусы деп аталады.
Қисықтың кезкелген жазықтығында қисықтың радиусы төмендегі формуламен анықталады:
(17)
(17) теңдеуін меридиан эллипсіне қолдана отырып (2) теңдеуімен, дифференциалдағаннан кейін және сәйкесінше туындылардан кейін алатынымыз:
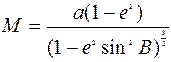(18)
N шамасының мәнін анықтау үшін келесі теореманы қолданамыз: егер эллипсоидтың екі нүктесінде екі қилысу кездесетін болса, онда екеуіне ортақ жанасатын сызықтың біреуіне тігінен, ал екіншісіне иілген болса, қисықтың радиусы қарапайым қима шамасына тең болады, яғни қиынды арасындағы косинус бұрышына тең болады,
Сурет 10
Осы жағдайда (Сурет 10) қараймыз:
(19)
Мұнда z- параллел радиусы;
N- бірінші вертикалдың қисығы;
В- геодезиялық ендік;
Суреттегіден (10) шығатыны
(20)
(19) бен (20) формулаларынан алатынымыз
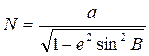(21)
Қисықтың орташа радиусы эллипсоидтың бірілген нүктесінде төмендегі формуламен анықталады:
(22)
Ал қисықтың радиусының қимасы А туынды азимутының қимасымен анықталады.
(23)
№1 Референц-эллипсоиданың бетін қолдана отырып, әртүрлі геодезиялық есептерді шешу
Берілген нүктедегі эллипсоид бетінің басты қисық радиусының координаттар жүйесі арасындағы байланыс.
Геодезиялық ендігі B=53°54'30" + 10"·n болатын нүкте үшін есептеу қажет:
1. формула бойынша тікбұрышты координатты х у меридиан эллипсінің жазықтығында:
2. Ф геоцентрлік ендікті төмендегі формуламен:
` 
 |
3. U келтірілген ендікті төмендегі формуламен:
 |
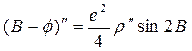4. меридиан эллипсінің қисық радиусы Μ төмендегі формуламен:
5. бірінші вертикал қиманың радиусын Nтөмендегі формуламен:
 |
6. қисықтың орташа радиусы R төмендегі формуламен:
7. азимутпен қилысқан қисықтың радиусын А = Ι24°36 45" + 30"·n
8. 5" ендікті өлшеу кезінде қисықтың радиусының өсімшесін М дифференциал арқылы анықтау керек.
ҮЛГІ
Ғимараттарды есептеу мен өңдеу (нөлдік нұсқа)
Бастапқы берілгендер: a= 6378245.Ом
е2 =0,0066934216
ρ- 206264,81" -
B= 53°54'30"
I. тікбұрышты координаттарды анықтау х, у.
| cosB a cosB | 0.5890788 3757289.10 |
sin B
sin2B
e2sin2B
1-e2sin2B
| 0.8080755 0.60529861 0.0047069 0.99562931 0.9978122 |
| x | 3765527.10 |
1-e2
a (1-e2)
| 0.9933065784 6335552.72 0.9978122 |
| y | 5130829.70 |
2. геоцентрлік ендікті есептеу
| tgB (1-e2) | 1.3713613 0.9933066 |
| tg ф ф | 1.3625795 53043'29.9" |
| E2/2 p " 2B sin2B | 0,00334671 206264.81 107049'00" 0.9520404 |
| (B-ф)" ф | 657.20"=10'57.20'' 53043'32.80'' |
3. келтірілген ендікті есептеу
| 1-e2 tgB | 0.9966476 1.3717613 |
| tgU U | 1.3671627 53049'00.12'' |
2. меридианның қисық радиусын есептеу.
  а(1-е2)
| 6335552.20 0,9978122 0.9934509 |
| M | 6377317.50 м |
3. бірінші вертикал радиус қисығын есептеу.
 α
| 6378245.0 0.9978Ι22 |
| N | 6392229.90 м |
6. қисықтың орташа радиусын есептеу,
| √M √N | 2525,3351 2528,2859 |
| R | 6384769.10 |
7. азимутпен қилысқан қисықтың радиусын есептеу
А = 124°36'45"
| cos A cos2A Ncos2A | - 0.5680233 0.3226504 2062456.00 |
| Sin A Sin2M MSin2A | 0.8230Ι24 0.6773495 4319672.90 |
| p A | 6387410.60 м |
8. М нүктесін β сәйкес есептеп шығарып бастапқы мәндеріне қою үшін (.18) формуласын дифференциалдау қажет.
| (B-U)'' | 328.60''=5'28.60'' |
| U | 53049'01.40'' |
2. ЕКІ МЕРИДИАН МЕН ПАПАЛЛЕЛДЕРДІҢ ҰЗЫНДЫҒЫН ЕСЕПТЕУ
Сферадағы тұрақты радиустың доға ұзындығын есептеген кезде белгілі формуланы қолданады;
• S= R.- ạ, (1)
мұнда R - сфера радиусы;
a - іздеп отырған доғаның орталық бұрышы.
Параллель дөңгелек шама болғандықтан, (I,) формуласы бойынша бойлықтар белгілі пункттер арасындағы параллель доғасын еспептеу, төмендегі формулаға сәйкес болады:
(2)
мұнда z- параллелдер радиусы;
L - пункттердің бойлығы;
ρ".- 205264,81"
г параллельдер радиусы белгілі болғандықтан, төмендегі формула бойынша есептеледі
 |
(3)
Мұнда a - референц-эллипсоидтың үлкен жарты осі;
e2- меридина эллипсінің бірінші эксцентриситетінің квадраты;
β – параллельдің геодезиялық ендігі,
Меридиан доғасының ұзындығын (I) формуласымен есептеу, тек шексіз кішкентай доғалар болған жағдайда, жалпы жағдайда меридиан доғасы төмендегі формуламен есептеледі:
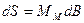(4)
мұнда M m – есептеп отырған қисық радиусы доғасыныңорташа интегралды мәні;
db – геодезиялық ендіктің доға бойымен өсуі.
Меридиандар доғасының ұзындығын есептеген кезде соңғы ұзындығын (4) есептелуі бойынша доға ұзындығын түгелдей интегралдау қажет.
 |
(5)
Интегралданған функция элементарлы функциялар үшін қайта интегралдануы мүмкін емес, сондықтан интегралданған функцияны интегралдау үшін дәрежелі қатарға қояды, артыан әр мүшесін жеке-жеке интегралдайды. Интералдағаннан кейін кез келген меридианның доғасының ұзындығын есептеу үшін төмендегі есептеу қолданылады:
мұнда А,В,С,Д - е 2 дәрежесіне қатысты, берілген референц-эллипсоидтың коэффициенттері.
Арнайы жеке есептеулер кезінде (6) формуласы жеңілдетілген болады.
I. Экватордан меридиан ұзыдығын анықтаған кезде берілген нүктеден ендігі белгілі (геодезиялық кесте құрған кезде) B1 = 0 болса, онда sin2B1=sin4B1=sin6B1=0, (6) формула келесі түрде болады
 |
(7)
a, е2, А,В,С, Д сандық мәндерін қойғаннан кейін:
 |
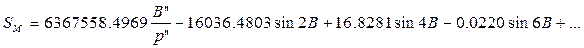(8)
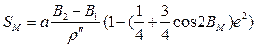2. Градустық өлшеулерді өңдеу кезінде эллипсоидтың жерлік өлшемін анықтау мақсатында (6) формуласы төмендегідей өзгереді:
(9).
1. Қабырғалары 400 км болатын триангуляциялардың өңдеу кезінде
(10)
мұнда ММ- өлшенетін доға бойы қисығының орташа радиусы. Бұл өлшем төмендегі формуламен анықталады:
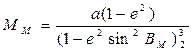
(11)
мұнда
(12)
4. Қабырғалары 45 км тең болатын триангуляциларды өңдеу кезінде
 |
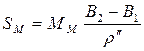(13)
5. Ұзындығы 1000 км тең болатын доғаның ұзындығын анықтау кезінде Симпсон формуласын қолдануға болады
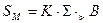(14)
мұнда 
(15)
(16)
(17)
Шамалы арақашықтықта (14) формуласы доғаның ұзындығын есептеуде 1-2 см дәлдікпен өлшеуді қамтамасыз етеді.
Сондықтан, меридиан доғасының ұзындығын анықтау кезінде ендікке байланысты келесі формулалар қолданылуы мүмкін (8), (9), (10), (13), (14).
