Алгебра. 10 сынып.
Сабақтың тақырыбы: Туынды тарауын қайталау.
Сабақтың мақсаты: Оқушылардың туынды тарауы бойынша теориялық білімдерін, дифференциалдау ережелерін қолдануға, жанама теңдеуін жазуға, функцияны зерттеуге, күрделі функцияның туындысын табуға, есептер шығарту арқылы білімдерін тексеру
Сабақтың түрі: білімді тиянақтау сабағы.
Сабақтың әдісі: СТО технологиясы.
Күтілетін нәтиже:
1. Туынды табу ережелерін, формулаларын есептер шығаруда қолдана алады.
2. Өмірмен байланысты есептерді туынды көмегімен зерттей алады.
3. Туындысы бойынша функцияны таба біледі.
Бағалау:
Формула, ережені жатқа білу.
Ауызша есеп шығаруы.
Тестпен жүмыс жасауы.
Көрнекілігі: Power Point-та слайд,
интерактивті тақта,
плакаттар;
таблицалар,
формулалар.
Сабақтың барысы.
І. Қызығушылықты ояту.
Мұғалім: Сәләмәтсіздер де, оқушылар! Бүгін біздер туынды тарауын қайталаймыз. Алдыменен туынды туралы білімдерімізді жинақтап алайық. Туынды ассоциациясын толтырыңдар.
 |
Енді, формулаларға кезек берейік. Төмендегі формулаларды жалғастырыңдар.
1. 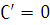 6.
6.  =
= 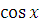
2.  7.
7.  =
= 
3. 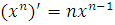 8.
8. 
4.  9.
9.  =
= 
5. 
осы формулаларды оқушылар өз беттерімен қорытып дәлелдейді.
Ауызша есептер:
1. f(x) =cos x2. Жауабы: -2хsinx2
2. f(x) = (1-2х)(2х+1) функциясы берілген. f ¢(0,5) есептеңіз. Жауабы: -4
3. f(x) = sin 5x cos 6x+cos 5x sin 6x туындысын тап. Жауабы: 11cos11х
4. f(x) =2x3 – 5x функциясының графигіне М(2;6) нүктесінде жүргізілген жанаманың көлбеулік бұрышының тангенісін табыңдар.
Жауабы: tqα=19
5. f(x) =(8х5-5х8)12 күрделі функциясының туындысын тап. Жауабы: 480(8х5-5х8)11(х4-х7)
II.Мағынаны тану:
Оқушылар өздері дайындаған слайдтары арқылы
1. Туындының көмегімен функцияның өсу,кему аралығын табу,
2.Функцияның ең үлкен, ең кіші мәнін табу,
3. Жазбаша есептерге туындыны қолдану
жұмыстарын көрсетті.
Сыныпта шығарылатын есептер:
1)  функциясының
функциясының
а) нөлдерін Жауабы: а) (1; 0), (-1; 0); б) жоқ; в) (-∞; 0),(0;+∞)
б) өсу аралығын
в)кему аралығын тап.
2)f (x) = x² -12x +27 функциясының [3;7] аралығында ең үлкен, ең кіші мәндерін тап. Жауабы: fмах(3)=0, fmin(6)=-9.
3)  функциясының
функциясының
а)барлық сындық нүктелерін Жауабы: а) х=-2; 2, б) хмах=2, хmin=-2.
б)минимум, максимум нүктелерін тап.
4)Бүйір қабырғасы 1-ге тең болатын дұрыс төртбұрышты пирамида көлемінің ең үлкен мәнін табыңыз.
Жауабы:
Пирамиданың көлемінің формуласы:  (1)
(1)
Біздің есебімізде, бүйір қыры 1-ге тең болғандықтан ол келесі түрде жазылады: 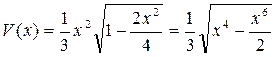 (2)
(2)
Осы функцияның туындысын тауын, нөлге теңестіріп, теңдеуді шешеміз:
4х3-3х5=0. Осыдан х2= 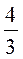 ; H=
; H= 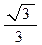 , (1), (2) формуланы пайдаланып, орнына қойсақ,
, (1), (2) формуланы пайдаланып, орнына қойсақ, 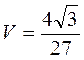 шығады.
шығады.
ІІІ. Ой толғаныс. Тест бойынша оқушылар бағаланады.
ТЕСТ
1. Туындыны тап 
A) 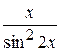
B) 
C) 
D) 
E) 
2. Абсциссасы х = 0 нүктесінде f(x) = 5x3 + 9x - 27 функциясының графигіне жанама жүргізілген. Жанама мен Ох осінің қиылысу нүктесінің абсциссасын табыңыз.
A) 3
B) 2
C) 1
D) 4
E) -2
3. Функцияның туындысын табыңыз: f(x) = 
A)  .
.
B) -  .
.
C) 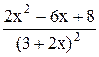 .
.
D) 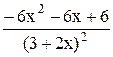 .
.
E) -x.
4. f(x) =  функциясы берілген. f ¢(-2) есептеңіз.
функциясы берілген. f ¢(-2) есептеңіз.
A)  .
.
B)  .
.
C) -4.
D)  .
.
E) 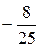 .
.
5. у = 2x2 - 1 функциясының графигіне x0 = 3 нүктесінде жүргізілген жанаманың теңдеуін жазыңыз.
A) y = 2x - 1.
B) y = 9x - 13.
C) y = 12x - 19.
D) y = 4x + 5.
E) y = 18x - 19.
Тесттің жауаптары:
1)д; 2)а; 3)б; 4)е; 5)с
Үйге тапсырма: Үйге № 231, 232.
Тесттер жинағы 2011ж, нұсқа 7,8,9,10 №17,18.
Орытындылау.
Мұғалім: Дифференциалдау амалы 11 сыныпта интеграл тақырыбында жалғасын табады. Дифференциалдау амалы интегралдау амалына кері амал болып табылады.
Оқушыларды бағалау.
Жалғамалар:










