ЛАБОРАТОРНАЯ РАБОТА №5
По дисциплине: «Технология Цифровой Связи»
Тема: «Простые межсимвольные помехи»
Специальность: Радиотехника, электроника и телекоммуникации
Выполнили: Нурахмет Д., Ауелханулы О., Сарсумбеков Т. Группа: РЭТ 13-5
Приняла: асс. Аширбаева С. М.
____________________________ «____» _______________2016г.
Алматы 2016
Цель работы
Исследовать явление межсимвольной интерференции в простом канале связи; построение глазковой диаграммы; изучить методы, применяемые в технике связи для устранения и уменьшения МСИ.
Рабочее задание
I. Исследование передачи сигналов при идеальной фильтрации.
II. Построение глазковой диаграммы.
III. Исследование явления межсимвольной интерференции в простом канале.
IV. Исследование методов уменьшения и устранения межсимвольной интерференции путем использования фильтров типа приподнятого косинуса.
Выполнение работы
Межсимвольная интерференция.
Ограничение спектра сигнала в каналах связи, нелинейность частотных характеристик вызывают появление переходных процессов, которые искажают или расширяют импульсный сигнал, проходящий через канал. Если ширина полосы канала приблизительно равна ширине полосы сигнала, то искажение будет превышать длительность передачи символа и приведет к наложению импульсов сигнала (единичные элементы сигнала, растягиваясь во времени, перекрываются соседними элементами). Этот эффект называется межсимвольной интерференцией (МСИ, intersymbolinterference - ISI). Это влечет за собой появление колебаний амплитуды принимаемых импульсов и, следовательно, снижает помехоустойчивость передачи дискретной информации. При больших искажениях частотных характеристик передача оказывается невозможной даже при отсутствии помех.
Идеальная фильтрация по Найквисту.
Исследованием проблемы предотвращения появления МСИ при приеме долгое время занимался Найквист. Он показал, что минимальная теоретическая ширина полосы системы, требуемая для детектирования Rs символов/секунду без МСИ, равна Rs/2 Гц. Это возможно, если передаточная функция системы H(f) имеет прямоугольную форму, как показано на рисунке 4.1, а. Для низкочастотных систем с такой H(f), односторонняя ширина полосы фильтра равна 1/2Т (идеальный фильтр Найквиста), импульсная характеристика функции H(f) имеет вид h(t)=sinc(t/T) (см. рисунок 4.1, б). Импульс, описываемый функцией sinc(t/T), называется идеальным импульсом Найквиста; он имеет бесконечную длительность и состоит из многочисленных лепестков: главного и боковых, именуемых хвостами. Найквист установил, что если каждый импульс принятой последовательности имеет вид sinc(t/T), импульсы могут детектироваться без МСИ. Это условие называют первым условием Найквиста. Оно выполняется для импульса, который только в некоторый момент отсчета имеет отличное от нуля характеристическое значение и нулевые значения во всех остальных отсчетных точках. Следовательно, предполагая идеальную синхронизацию процесса взятия выборок, получаем, что МСИ не будет влиять на процесс детектирования сигнала, несущие которых сдвинуты по фазе на 90о.
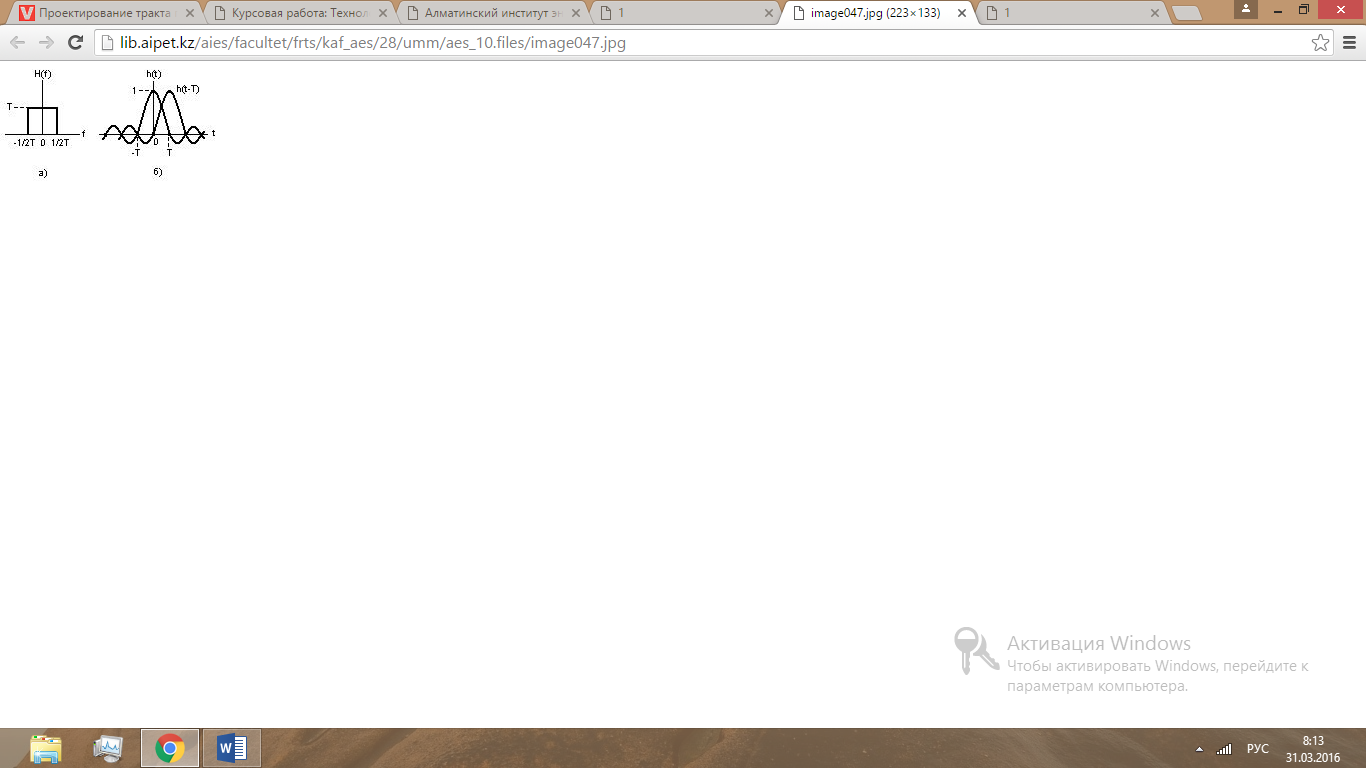
а) прямоугольная передаточная функция системы H(f);
б) принятый импульс h(t)=sinc(t/T).
Рисунок 1 – Каналы Найквиста для нулевой межсимвольной интерференции
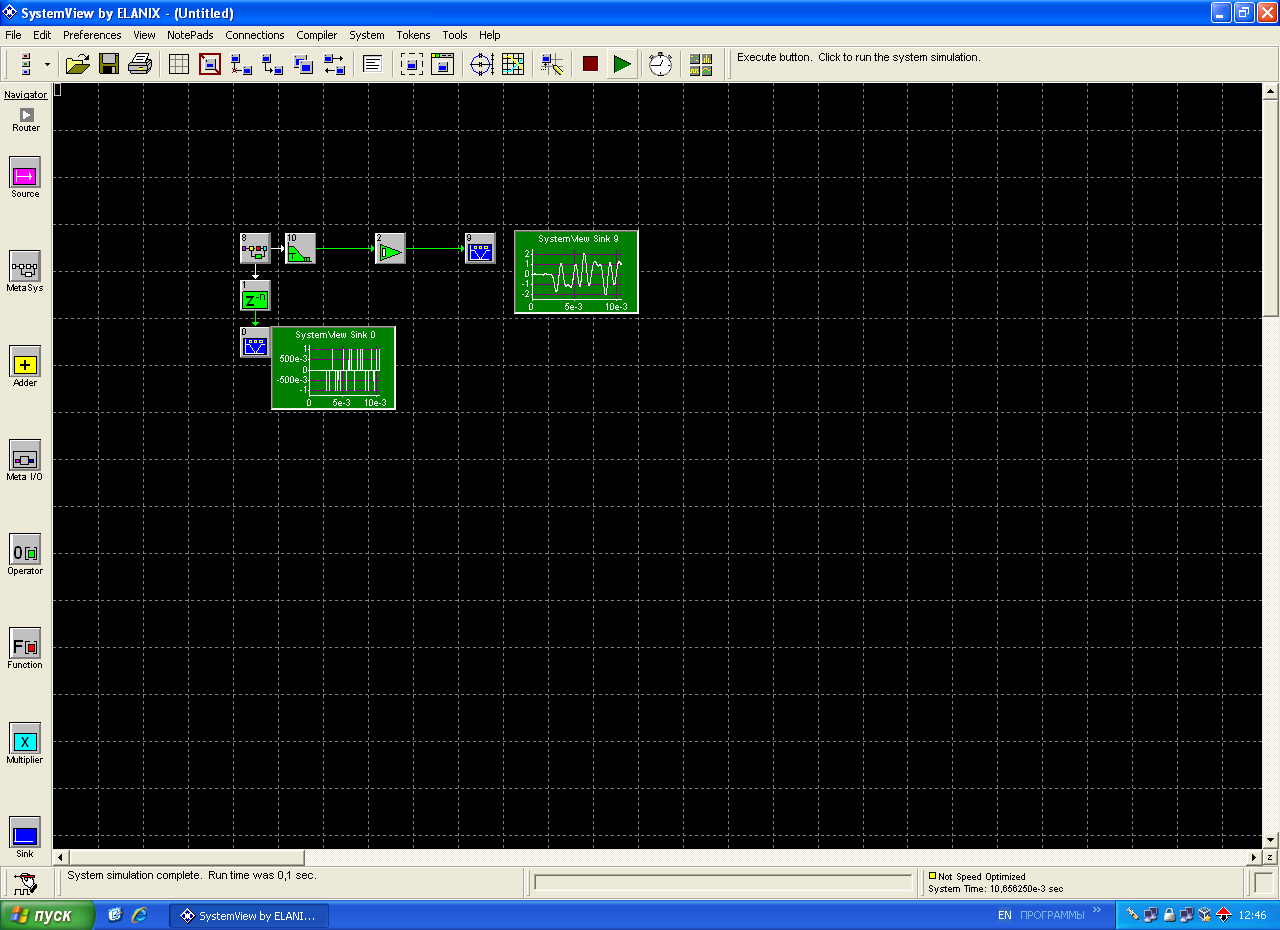
Рисунок 2 – Последовательность импульсов со скоростью передачи 2400 бит/секунду принимает форму импульса sinc(t/T).






