Для анализа свойств и характеристик случайного процесса, а также различных его преобразований необходимо задать математическую модель случайного процесса. Такая модель может представлять собой описание возможных реализаций случайного процесса в сочетании с указанием относительной частоты их появления. Приведем несколько примеров моделей случайных процессов, задаваемых таким образом.
X1 (t)
 |
t1 t2 t
x2(t)
t1 t2 t
x3(t)
t1 t2 t
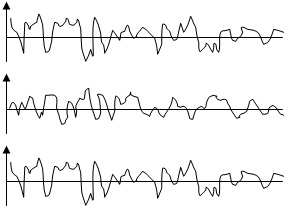
Рисунок 6.1-Реализации случайных процессов
Гармонический сигнал со случайной начальной фазой
Во многих практических задачах используется модель случайного процесса, реализации которого представляют собой гармонические колебания с известными (детерминированными) амплитудой и частотой, но случайной начальной фазой. Таким образом, реализация рассматриваемого случайного процесса может быть записана как

где А – амплитуда (детерминированная), ω0 – частота (детерминированная) и φ – случайная начальная фаза, которая в большинстве практически интересных случаев может считаться равномерно распределенной на интервале 0…2π, то есть имеющей следующую плотность вероятности:

Графики нескольких реализаций данного случайного процесса, представляющие собой синусоиды, смещённые друг относительно друга по временной оси, показаны на рисунке 6.2.
 x(t)
x(t)
0 t
Рисунок 6.2- Реализация гармонического сигнала со случайной начальной фазой
Как видите, конкретный вид реализации процесса в данном случае определяется значением всего лишь одной случайной величины – начальной фазы.
Случайный телеграфный сигнал. Таким сигналом назван случайный процесс, реализации которого принимают значения +1 и -1, причем перепады уровня происходят в случайные моменты времени и число N перепадов уровня, происходящих за время τ, является случайной величиной с дискретным распределением вероятности, описываемым законом Пуассона:
 (6.1)
(6.1)
Здесь λ – неотрицательный параметр, определяющий среднюю частоту возникновения перепадов уровня.
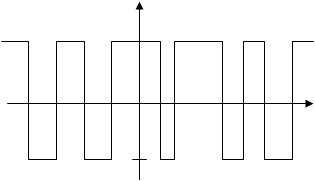
Скачки уровня происходят в случайные моменты времени tk, поэтому аналитически записать формулу для отдельной реализации данного случайного процесса оказывается весьма затруднительно, а изобразить ее график можно лишь условно рисунок 6.3.
 x(t)
x(t)
t
-1
Рисунок 6.3-Реализация случайного телеграфного сигнала
В данном случае конкретная реализация задается бесконечным множеством случайных величин – моментов перепадов уровня tk, а характеристики случайного процесса определяются статистическими свойствами этих случайных величин.
Итак, полное описание случайного процесса дает его ансамбль реализаций. Однако для решения практических задач часто достаточно более простых характеристик, выражающихся в виде числовых параметров и детерминированных функций. Об этом пойдёт речь далее.






