В условиях отсутствия помех скорость передачи информации определяется количеством информации, переносимым символом сообщения в единицу в единицу времени равна: С =n * H
n –количество символов, вырабатываемых источником сообщений за единицу времени, Н – энтропия снимаемая при получении одного символа сообщения.
Техническая скорость
V=1/τ (симв/сек),
Где τ- время передачи одного символа вторичного алфавита.
Тогда, для сообщений составленных из равновероятных взаимонезависимых символов равной длительности скорость передачи информации
С=(1/τ) * log2 m (бит/сек).
В случае неравновероятных символов равной длительности
С= 
(бит/сек).
Пропускная способность (или емкость канала связи) есть максимальная скорость передачи информации по данному каналу связи:
(бит/сек).
Для двоичного кода:
(бит/сек).
При наличии помех пропускная способность канала связи вычисляется как произведение количества принятых в секунду знаков n на разность энтропии источника сообщений и условной энтропии:
Cn=n*[H(A)-H(A/B)]
или
Cn=n*[H(B)-H(B/A)]
Информационные потери при передачи сообщений по каналам связи с шумами
Среднее Количество информации, содержащееся в принятом ансамбле сообщений
а) с помощью энтропии объединения
І(А,В)=Н(А)+Н(В)-Н(А,В) (4,4)
б) с помощью условной энтропии:
І(А,В)=Н(А)-Н(А/В) (4.5)
Смысл выражения: Н(А)- энтропия источника,
Н(А/В) – среднее количество информации потерянное в канале из-за ошибок.
І(А,В)=I(В,А) (4-6)
Из формул (4.4)- (4.5) можно вывести формулу удобную для расчетов:
(4.7)
Дифференциальная энтропия
На практике множество возможных состояний источника информации составляет континуум, т.е. источники – непрерывные.
Определим энтропию непрерывного источнмка информации следующим образом: разобъем диапозон изменения непрерывной случайной величины
U, на конечное число п малых интервалов Cu. Поскольку Cu мало, вероятность р (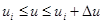
) реализации значения u из интервалаui, ui+Cu:
p()=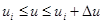 
Тогда энтропия дискретной случайной величины U может быть задана в виде
или
Так как
то
По мере уненьшения 
р (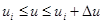), всё больше приближается к вероятности р(
) равной нулю, а свойства дискретной величины U - к свойствам непрерывной случайной величины U. Переходя к пределу при 
0 получаем следующее выражение для энтропии H(U) непрерывного источника:
или
(3,4)
Эта величина при 0 стремится к бесконечности, что полностью соответствует определению о том, что неопредленность выбора из бесконечно большого числа возможных состояний (значений) бесконечно велика.
Первый член в правой части соотношения (3.4) - конечное значение, которое зависит только от закона распределения непрерывной случайной величины U и независит от шага квантования Cu.
Второй член того же соотношения зависит лиш от шага квантования случайной величины U, из-за него H(U) обращается в бесконечность.
Один из подходов для получения конечной характеристики информационных свойств непрерывного источника состоит в том, что в качестве неопределенности непрерывного источника принимают первый член соотношения (3.4):
(3.5)
Она получила название относительной дифференциальной энтропии или просто дифференциальной энтропии непрерывного источника информации.
Свойства дифференциальной энтропии:
а. Если единственным ограничением для случайной величины U являетсяобласть её возможных значений 
, то максимальной дифференциальной энтропией обладает равномерное распределение вероятностей в этой области.
б. Если ограничения на область значений непрерывной случайной величины U отсутствует, но известно, что дисперсия её ограничена, то максимальной дифференциальной энтропией обладает нормальное распределение величины U.
Основная литература:2[111-119J; 3(109-114]; 9J44-46].
Контрольные вопросы:
1. Как связаны между собой понятия количества информации и энтропия?
2. Определите понятие избыточности.
3. Определите количество информации в сообщении, составленном из к неравновероятных символов.
4. Дайте определение дифференциальной энтропии и сформулируйте её основные свойства.
