Практикум по дифференциальной геометрии и топологии
Аудиторная работа № 9
Тема: Понятие поверхности. Способы задания поверхностей (продолжение)
3. Дан открытый сферический треугольник, высекаемый на сфере радиуса 2 с центром в точке О трехгранным углом ОАВС с прямыми плоскими углами при вершине.
1) Запишите его скалярные и векторное параметрические уравнения в декартовых координатах х, у, z, совмещая положительные полуоси Ох, Оу, Оz с лучами ОА, ОВ, ОС соответственно, и выбирая параметры u и v точки поверхности также, как и в упражнении 2.
2) Является ли полученная параметризованная поверхность регулярной, если «да», то какого класса регулярности?
3) Найдите внутренние координаты точки Р (1; 1;  ) сферического треугольника относительно этой параметризации.
) сферического треугольника относительно этой параметризации.
4) Запишите уравнения координатных линий, проходящих через нее, во внутренних координатах u, v и параметрические уравнения в декартовых координатах х, у, z.
5) Изобразите эти координатные линии на рисунке, а также их прообразы в параметрической плоскости.
Ответ: 1) х = 2cosu cosv, y = 2cosu sinv, z = 2sinu, (u;v)  (0;
(0;  ) х (0;
) х (0;  );
);
 = (cosu cosv; cosu sinv; sinu), (u;v)
= (cosu cosv; cosu sinv; sinu), (u;v)  (u;v)
(u;v)  (0;
(0;  ) х (0;
) х (0;  ).
).
2)  .
.
3) Р (u =  , v =
, v =  ).
).
4) u =  , v =
, v =  ; х =
; х =  cosv, y =
cosv, y =  sinv, z =
sinv, z =  , где v
, где v  (0;
(0;  ), х =
), х =  cosu, y =
cosu, y =  cosu, z = 2sinu, где u
cosu, z = 2sinu, где u  (0;
(0;  ).
).
4. Параметризуйте в декартовых координатах х, у, z открытый сферический треугольник из упражнения 3, введя систему координат Охуz аналогичным образом и взяв в качестве параметров произвольной точки этой поверхности ее абсциссу p и ординату q. Является ли данная параметризованная поверхность регулярной, если «да», то какого класса?
Ответ: х = p, у = q, z = 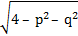 , где
, где  < 4, p
< 4, p  0, q
0, q  0.
0. 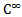 .
.
Упражнения для домашней работы
3. Дан открытый сферический треугольник, высекаемый на единичной сфере с центром в точке О трехгранным углом ОАВС с прямыми плоскими углами при вершине.
1) Запишите его скалярные и векторное параметрические уравнения в декартовых координатах х, у, z, совмещая положительные полуоси Ох, Оу, Оz с лучами ОА, ОВ, ОС соответственно, и выбирая параметры m и n точки поверхности также, как и в упражнении 2.
2) Является ли полученная параметризованная поверхность регулярной, если «да», то какого класса регулярности?
3) Найдите внутренние координаты точки М ( ;
;  ;
; 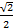 ) сферического треугольника относительно этой параметризации.
) сферического треугольника относительно этой параметризации.
4) Запишите уравнения координатных линий, проходящих через нее, во внутренних координатах m, n и параметрические уравнения в декартовых координатах х, у, z.
5) Изобразите эти координатные линии на рисунке, а также их прообразы в параметрической плоскости.
Ответ: 1) х = sin m sin n, y = sin m cos n, z = cos m, где (m; n)  (0;
(0;  ) х (0;
) х (0;  );
);
 = (sin m sin n; sin m cos n; cos m), где (m; n)
= (sin m sin n; sin m cos n; cos m), где (m; n)  (0;
(0;  ) х (0;
) х (0;  ).
).
2)  .
.
3) М (m =  , n =
, n =  ).
).
4) m =  , n =
, n =  ; х =
; х = 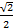 sin n, y =
sin n, y = 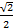 cos n, z =
cos n, z = 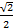 , где n
, где n  (0;
(0;  ), х =
), х = 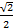 sin m, y =
sin m, y = 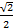 sin m, z = cos m, где m
sin m, z = cos m, где m  (0;
(0;  ).
).
4. Параметризуйте в декартовых координатах х, у, z открытый сферический треугольник из упражнения 3, введя систему координат Охуz аналогичным образом и взяв в качестве параметров произвольной точки этой поверхности ее ординату s и аппликату t. Является ли данная параметризованная поверхность регулярной, если «да», то какого класса?
Ответ: х =  , у = s, z = t, где
, у = s, z = t, где  < 1, s
< 1, s  0, t
0, t  0.
0. 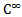 .
.
Дополнительные задания (для желающих)
1. Являются ли параметризации  = (2cosu cosv; 2cosu sinv; 2sinu), где (u;v)
= (2cosu cosv; 2cosu sinv; 2sinu), где (u;v)  (0;
(0;  ) х (0;
) х (0;  ), и
), и  = (p, q,
= (p, q, 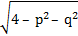 ), где
), где  < 4, p
< 4, p  0, q
0, q  0, рассмотренного ранее сферического треугольника, эквивалентными? Если «да», то какого класса? Задайте формулами диффеоморфизм замены параметров u, v на параметры p, q.
0, рассмотренного ранее сферического треугольника, эквивалентными? Если «да», то какого класса? Задайте формулами диффеоморфизм замены параметров u, v на параметры p, q.
Ответ. Да.  . p = 2cosu cosv, q = 2cosu sinv, где (u; v)
. p = 2cosu cosv, q = 2cosu sinv, где (u; v)  (0;
(0;  ) х (0;
) х (0;  ).
).
2. Дана открытая единичная полусфера, центр которой совпадает с началом декартовой системы координат Охуz, проходящая через точку (0; 0; 1). Задайте ее: а) неявно; б) явно; в) параметрически в указанных координатах.






