Основные теоретические положения. Федеральное агентство по образованию Российской Федерации

Федеральное агентство по образованию Российской Федерации

Филиал «Севмашвтуз» государственного образовательного учреждения высшего профессионального образования «Санкт – Петербургский государственный морской технический университет»

В г. Северодвинске

 

 

ФАКУЛЬТЕТ: IV

КАФЕДРА: ФИЗИКИ

 

 

ЛАБОРАТОРНАЯ РАБОТА

 

Изучение законов колебания математического и физического маятников

 

 

Северодвинск

ЛАБОРАТОРНАЯ РАБОТА ФМ - 13

Изучение законов колебания математического и физического

маят­ников

Цели работы

1. Изучить теорию гармонических колебаний математического и физического маятников.

2. Определить ускорение свободного падения.

3. Определить период собственных колебаний математического и физиче­ского (оборотного) маятников.

3. Определить положение центра масс физического маятника.

 

Основные теоретические положения

 

В физике под маятником понимают твердое тело, совершающее под дейст­вием силы тяжести колебания вокруг неподвижной точки или оси. Принято раз-ли­чать математический и физический маятники.

Математическим маятником называют идеализированную систему из не­весомой и нерастяжимой нити, на которой подвешена масса, сосредоточен­ная в одной точке.

Достаточно хорошим приближением к математиче­скому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тон­кой нити.

Отклонение маятника от положения равновесия будем характеризовать уг­лом , об­разованным нитью с вертикалью (рис. 1).

При отклонении маятника от положе­ния равновесия возникает вращатель­ный момент силы тяжести , равный по модулю произведению силы mg на её плечо = l sin :

|M| = mgl sin ,

где m - масса; l - длина маятника.

Рис. 1

Момент M стремится вернуть ма­ятник в положение равновесия и аналогичен в этом отноше­нии квазиуп­ругой силе. Поэтому так же, как смеще­нию и квазиупругой силе, моменту M и угло­вому смещению нужно приписы­вать противоположные знаки. Следовательно, вы­ражение для вращатель­ного момента имеет вид

M = - mgl sin . (1)

Напишем для маятника уравнение динамики вращатель­ного движения, обо­зна­чив угловое ускорение через и учиты­вая, что момент инер­ции маят­ника ра­вен

I = ,

получаем

I ε = M или = - mgl sinφ.

Последнее уравнение можно привести к виду

+ sin = 0. (2)

Ограничимся рассмотрением малых колебаний. В этом случае можно поло­жить sin .

Введя, кроме того, обозначение

= , (3)

придем куравнению

+ = 0, (4)

решение которого имеет вид

= cos( t + ). (5)

Следовательно, при малых колебаниях угловое отклонение математиче­ского маятника изменяется со временем по гармоническому закону.

Как следует из (3), частота собственных колебаний математического маятника зави­сит только от длины маятника и от ускорения силы тяжести и не зависит от массы ма­ятника. Учитывая, что

,

с учётом (3) получаем формулу для периода коле­ба­ний математического маятника:

Т = 2 . (6)

Если колеблющееся тело нельзя представить как материальную точку, ма­ят­ник называется физическим. При отклонении физического маятника от по­ложения равно­весия на угол возникает вращающий момент M силы тяжести, стремя­щийся вер­нуть маят­ник в поло­жение равновесия:

M= - mga sin ,

где m - масса маятника; a - расстояние между точкой подвеса т. Ои центром масс т. С маятника (рис. 2). Знак “-“ имеет то же значение, что и в случае фор­мулы (1).

Обозначив момент инерции физического маятника относительно оси, проходящей через точку подвеса, буквой I, запишем для него основ­ное уравне­ние динамики вращательного движения:

Рис. 2

= M или I = - mga sin . (7)

В случае малых колебаний (7) переходит в известное нам уравнение

+ = 0.

Через обозначена в данном случае величина

= mga/I. (8)

Из уравнений (7) и (8) следует, что при малых отклоне­ниях от положения рав­новесия физический маятник совер­шает гармонические колебания, частота ко­торых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром масс маятника. В соответствии с этим период коле­баний физического маятника определяется вы­ражением:

Т = 2 . (9)

Из сопоставления формул (6) и (9) получается, что математический маят­ник с длиной l, равной

l = 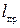= (10)

будет иметь такой же период колебаний, как и данный физический маятник. Вели­чину называют приведенной длиной физического маятника.

Таким образом, приведенная длина физического маятника - это длина такого матема­тического ма­ятника, период колебаний которого равен периоду колебаний данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см.точку О ' на рис. 2). Можно показать, что при под­ве­шивании маятника в центре качания О ' приведенная длина, а значит, и пе­риод ко­лебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр ка­чания обладают свойст­вом взаимности: при переносе точки подвеса в центр кача­ния прежняя точка подвеса становится новым центром качания.

На этом свойстве основано определение ускорения свободного падения с по­мощью так называемого оборотного маятника. Оборотным называется та­кой ма ­ ятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые он может поочередно подвеши­ваться.

Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маят­ника за любую из призм период колебаний был одинаков. Тогда расстояние между опор­ными ребрами призм будет равно 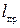. Измерив период колебаний маятника и зная 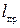, можно из формулы

Т = 2 . (11)

найти ускорение свободного падения g.