| Значение | Характер связи | Интерпретация связи |
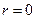
| Отсутствует | |
| Прямая | С увеличением  увеличивается 
|
| Обратная | С увеличением уменьшается , и наоборот
|
| Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
Пример. На основе выборочных данных о деловой активности однотипных коммерческих структур оценить тесноту связи между прибылью (тыс. руб.) 
и затратами на 1 руб. произведенной продукции 
.
Расчетная таблица для определения коэффициента корреляции
| №п/п | 
| 
| 
| 
| 
| 
| 
|
| 21 216 | 48 841 | 9 216 | -125 | ||||
| 1 070 | 82 390 | 1 144 900 | 5 929 | -993 | |||
| 1 001 | 77 077 | 1 002 001 | 5 929 | -924 | |||
| 53 934 | 367 236 | 7 921 | -517 | ||||
| 63 878 | 606 841 | 6 724 | -697 | ||||
| 63 909 | 622 521 | 6 561 | -708 | ||||
| Сумма | 4 466 | 362 404 | 3 792 340 | 42 280 | -3964 | ||
| Средняя | 744,33 | 83,67 | 60400,67 | 632056,67 | 7046,67 | -660,7 |
1. Используя формулу (2), получаем:
;
;
.
2. По формуле (4) значение коэффициента корреляции составило
.
3. По формуле (5) получаем:
.
.
Таким образом, результат по всем формулам одинаков и свидетельствует о сильной обратной связи между изучаемыми признаками.
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирические корреляционное отношение рассчитывается по данным группировки, когда 
характеризует отклонения групповых средних результативного показателя от общей средней:
,
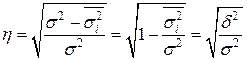где 
– корреляционное отношение;
– общая дисперсия;
– средняя из частных (групповых) дисперсий;
– межгрупповая дисперсия (дисперсия групповых средних).
Все эти дисперсии являются дисперсиями результативного признака.
Теоретическое корреляционное отношение определяется по формуле:
,
где 
– дисперсия выровненных значений результативного признака, т.е. рассчитанных по уравнению регрессии;
– дисперсия эмпирических (фактических) значений результативного признака.
, 
.
Тогда
объясняется влиянием факторного признака.
Корреляционное отношение изменяется в пределах от 0 до 1 
, и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции. Корреляционное отношение является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд показателей.
Коэффициент ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. При исследовании связи числовой материал располагают в виде таблиц сопряженности. Для вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).
Таблица для вычисления коэффициентов ассоциации и контингенции
| 
| 
|
| 
| 
|
| 
| 
|
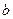
Коэффициенты определяются по формулам:
ассоциации
контингенции
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если 
или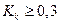 
.
Пример. Исследовалась связь между успеваемостью студентов-заочников одного из вузов и работой их по специальности. Результаты обследования характеризуются следующими данными:
Зависимость успеваемости студентов-заочников от работы их по специальности (цифры условные)
| Студенты-заочники | Число студентов | Из них | |
| Получившие положительные оценки | Получившие неудовлетворительные оценки | ||
| Работающие по специальности | |||
| Не работающие по специальности | |||
| Итого |
;
.
Таким образом, связь между успеваемостью студентов-заочников и работой их по специальности существенная.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона-Чупрова.
Вспомогательная таблица для расчета коэффициента взаимной сопряженности:
| У X | I | II | … |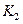 
| Всего |
| I | … |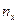 
| |||
| II | … |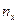
| |||
| … | … | … | |||
| … | … | … | … |
|
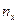
| Итого | 
|
| … |
| 
|
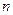
Эти коэффициенты вычисляются по формулам:
;
,
где 
– показатель взаимной сопряженности; определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы 1, получим:
.
– число значений (групп) первого признака; 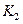– число значений (групп) второго признака. Чем ближе величины 
и 
к 1, тем связь теснее.
Пример: С помощью коэффициента взаимной сопряженности исследовать связь между себестоимостью продукции и производительностью труда:
| Себестоимость | Производительность труда | Итого | ||
| высокая | средняя | низкая | ||
| Низкая | ||||
| Средняя | ||||
| Высокая | ||||
| Итого |
, тогда 
, 
, 
, т.е. связь средняя.
