Практическая работа № 6
По дисциплине «Математика»
для студентов специальностей очно – заочного отделения
Тема: Вычисление неопределенного интеграла. Вычисление определенного интеграла.
Цель: Овладение методами вычисления неопределенных интегралов: непосредственного
интегрирования, методом подстановки и методом интегрирования по частям. Овладение методами вычисления определенных интегралов: непосредственного интегрирования, методом подстановки и методом интегрирования по частям.
Перечень необходимых сведений из теории:
1. Неопределенный интеграл, его свойства.
2. Метод подстановки в неопределенном интеграле.
3. Метод интегрирования по частям в неопределенном интеграле.
4. Определенный интеграл.
5. Основная формула интегрального исчисления.
6. Интегрирование методом подстановки в определенном интеграле.
7. Метод интегрирования по частям в определенном интеграле.
Образец выполнения задания:
Задание1: Найдите неопределенные интегралы и выполните проверку:
Решение: Найдем неопределенный интеграл, приведя подынтегральную функцию к удобному виду.
- Решение:
Найдем неопределенный интеграл, приведя подынтегральную функцию к удобному виду

Выполним проверку – найдем дифференциал семейства первообразных F(x)+C

2. Решение: Найдем неопределенный интеграл методом подстановки.
а) 
Выполним проверку – найдем дифференциал семейства первообразных F(x)+C
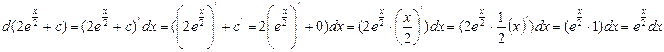
б) 
Выполним проверку – найдем дифференциал семейства первообразных F(x)+C

- Решение: Найдем неопределенный интеграл методом интегрирования по частям.
а) 
Выполним проверку – найдем дифференциал семейства первообразных F(x)+C

б) 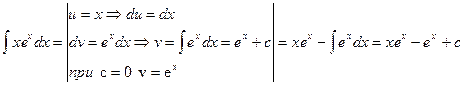
Выполним проверку – найдем дифференциал семейства первообразных F(x)+C

Задание 2: Вычислите определенный интеграл 
Решение:
.
Задание 3: Вычислите определенный интеграл, применяя метод подстановки 
Решение: 



Задание 4: Вычислите определенный интеграл, применяя метод интегрирования по частям 
Решение: 
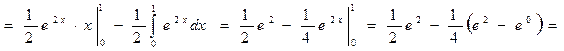

Задания для выполнения в аудитории: Найдите неопределённые интегралы функций:

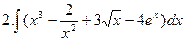




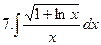



Вычислите определенный интеграл.
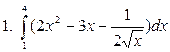






Задания для самостоятельного выполнения
Задание 1:
Найдите неопределенный интеграл. (1 и 2 примеры интегрируются с помощью таблицы интегралов, предварительно преобразовав подынтегральную функцию, 3 и 4 примеры интегрируются методом замены, 5 пример - интегрированием по частям)
Задание 2:
Вычислите определенный интеграл по формуле Ньютона-Лейбница.
Задание 3:
Вычислите определенный интеграл методом введения новой переменной.
Задание 4:
Вычислите определенный интеграл методом интегрирования по частям.
Исходные данные к заданию 1
| 1. | 2. | ||




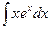
| 




| 


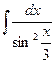

| 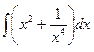
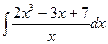

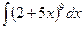

|
| 6. | |||


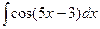


| 




| 


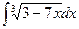

| 



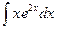
|
9. 
| 10. | ||





| 




|
Исходные данные к заданиям (2-4)
| 1 а) | 1 b) | 2 a) | 2 b) | ||
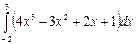
| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 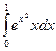
| 
| 
| |

| 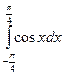
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 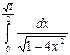
| 
| 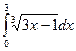
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 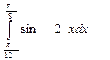
| 
|
В результате выполнения практической работы студент должен:
знать:
- определение неопределенного интеграла;
- метод интегрирование неопределенного интеграла заменой переменной;
- метод интегрирование неопределенного интеграла по частям;
- понятие определенного интеграла;
- теорему Ньютона-Лейбница;
- Интегрирование методом подстановки в определенном интеграле;
- метод интегрирования по частям в определенном интеграле;
уметь:
- вычислять неопределенный интеграл методом замены переменной;
- вычислять неопределенный интеграл, применяя метод интегрирования по частям.
- вычислять определенный интеграл по формуле Ньютона-Лейбница;
- вычислять определенный интеграл методом замены переменной;
- вычислять определенный интеграл, применяя метод интегрирования по частям.




