Все найденные элементы следует показать на первоначально заданных проекциях.
Эпюр выполняется на формате бумаги А3.
Примеры оформления задания приведены на рис.2.6.
Оформление основной надписи см. рис. 1.2 и 1.3.
Таблица 2.1 - Координаты точек для выполнения эпюра №2
| № задания | Точки | Координаты точек | № задания | Точки | Координаты точек | ||||
| X | Y | Z | X | Y | Z | ||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D | ||||||||
| A B C D | A B C D |
Решение задач эпюра №2
1. Построить проекции пирамиды. Определить видимость ребер пирамиды.
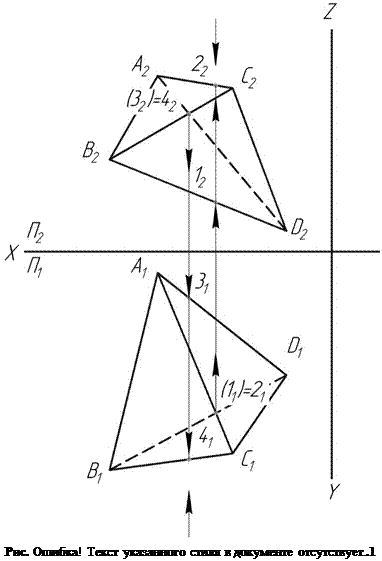Видимость ребер пирамиды определяется методом конкурирующих точек. На двух скрещивающихся ребрах AC и BD ставим две точки 1 и 2, проекции которых совпадают на горизонтальной плоскости проекций 11=21 (.Рис. 2.1).
Точки ставим там, где пересеклись проекции рёбер, которые в пространстве не пересекаются, но скрещиваются. Затем по линиям проекционной связи находим проекции точек 1 и 2 на фронтальной плоскости проекций на соответствующих ребрах А2С2 и B2D2. На фронтальной плоскости проекций одна из точек окажется выше (её координата Z больше), именно эта точка (точка 2) на горизонтальной плоскости будет видимой, так как на горизонтальную плоскость мы смотрим сверху. Точки 1 и 2 расположены на горизонтально-проецирующей прямой и являются конкурирующими. Та точка, которая оказалась невидимой обозначается на горизонтальной проекции скобками (1), и ребро, на котором она расположена, является невидимым и обозначается штриховой линией – ребро B1D1.
Видимость ребер на фронтальной плоскости определяется аналогично. Ставим на фронтальной плоскости 3=4, далее анализируем у какой из точек больше координата Y, именно эта точка (и ребро, на которой она расположена) будет видимым. Невидимое ребро обозначаем штриховой линией.
2. Методом замены плоскостей проекций определить величину двугранного угла между гранями ABC и DBC.
Плоскость проекций нужно поставить перпендикулярно общему ребру BC. В этом случае ребро спроецируется в точку, а пирамида спроецируется в виде треугольника, и можно будет измерить искомый угол.
Сначала заменяем плоскость П2 на плоскость П4 (см. Рис. 2.2).
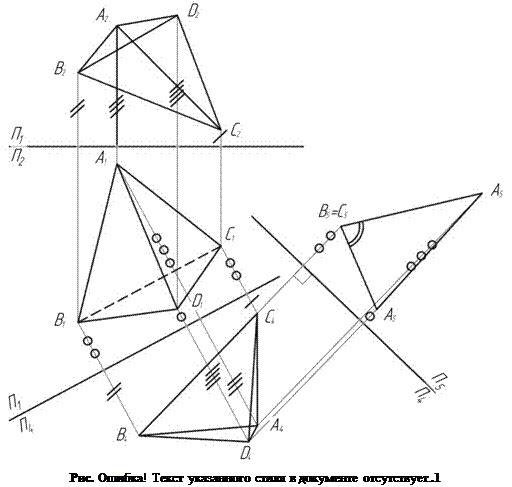Плоскость П4 ставим параллельно ребру ВС и перпендикулярно П1, ось П1/П4 проводим параллельно В1С1. Для всех точек проводим линии проекционной связи перпендикулярно оси П1/П4. В плоскости П4 от оси для точки А4 откладываем расстояние, равное расстоянию от оси П2/П1 до А2 в плоскости П2. На рисунке откладываемый отрезок обозначен тремя штрихами. Остальные точки В4, С4, D4 строим аналогично.
Затем заменяем плоскость П1 на П5. Плоскость П5 ставим перпендикулярно ребру ВС и перпендикулярно плоскости П4. Ось П4/П5 проводим перпендикулярно В4С4 на произвольном расстоянии от В4С4. Проводим линии проекционной связи и откладываем в плоскости П5 для каждой точки расстояния от плоскости П4 (от оси П4/П5), равные расстояниям в плоскости П1 от плоскости П4 (от оси П1/П4). Одинаковые расстояния отмечены на рисунке одинаковым количеством кружков.
Получаем вместо пирамиды треугольник, измеряем величину угла АВD, результат следует записать над основной надписью в виде Ð(DABC;DDBC) = XX°.
3. Вращением вокруг оси, перпендикулярной плоскости проекций определить расстояние от точки А до плоскости треугольника BCD.
Для того, чтобы «увидеть» и измерить на плоскости проекций расстояние от точки А до плоскости треугольника BCD, необходимо поставить треугольник перпендикулярно плоскости проекций. Треугольник спроецируется в виде отрезка, и можно будет опустить перпендикуляр из точки А и измерить его длину.
Как известно из курса школьной геометрии, две плоскости перпендикулярны, если прямая, лежащая в одной плоскости перпендикулярна второй плоскости. Проведем такую прямую в плоскости треугольника и повернем треугольник в пространстве так, чтобы эта прямая оказалась перпендикулярна плоскости проекций.
Примечание. Возможно в Вашем задании в треугольнике ВСD одна из сторон является горизонталью (фронталью). В этом случае дополнительную прямую проводить нет необходимости. Достаточно поставить сторону, являющуюся горизонталью (фронталью) перпендикулярно плоскости П2 (П1).
Проводим в треугольнике горизонталь ВН (Рис. 2.3). Проводим фронтальную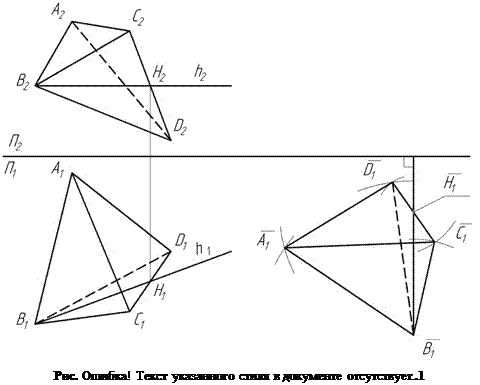 
 |
проекцию горизонтали h2 параллельно оси Х, на стороне C2D2 ставим Н2, затем строим горизонтальную проекцию горизонтали С1D1=h1. В удобном месте чертежа ставим горизонталь
= 
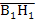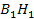перпендикулярно оси X. Достраиваем вокруг 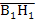треугольник 
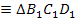.с помощью циркуля. Проводим линии проекционноц связи (Рис. 2.4). В плоскости П2 проводим от точек А2, B2, С2, D2 линии, параллельные оси Х, которые являются фронтальными следами плоскостей вращения для точек А, В, С, D. На пересечении следов плоскостей вращения и линий проекционной связи ставим фронтальные проекции повернутых точек 
, 
, 
, 
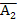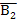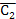. Если построение выполнено точно, то вершины треугольника 
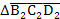должны лежать на одной прямой. Из точки 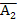опускаем перпендикуляр на прямую 
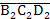. Ставим точку 
, измеряем расстояние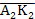 
, ответ записываем над основной надписью. Восстанавливаем все проекции точки К. Подумайте, как проводится 
.
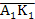4. Вращением вокруг горизонтали определить натуральную величину треугольника BCD.
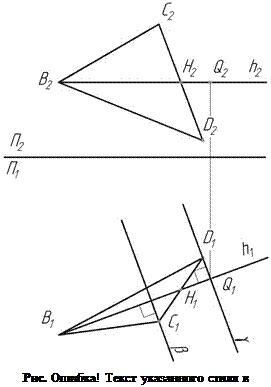В треугольнике BCD проводим горизонталь BН (Рис. 2.5). Сначала строим фронтальную проекцию горизонтали h2 паралллельно оси X, ставим точку H2 на отрезке C2D2, проводим линию проекционной связи на отрезок C1D1, ставим H1, далее проводим горизонтальную проекцию горизонтали h1. Горизонталь является осью вращения, следовательно точки B и Н при вращении остаются на месте. Для точек C и D строим плоскости вращения g и b, плоскости перпендикулярны оси вращения и перпендикулярны плоскости П1, то есть являются горизонтально-проецирующими.
Вращаем точку D (Рис. 2.6). Чтобы погрешность построений была меньше, нужно начать с той точки, которая расположена дальше от оси вращения. Горизонтальная проекция центра окружности вращения – точка Q1 – получается на пересечении горизонтального следа плоскости вращения g и проекции оси вращения h1. От точки Q1 на следе плоскости вращения нужно отложить натуральную величину отрезка QD. Натуральную величину QD определяем методом прямоугольного треугольника. Первый катет – Q1D1, второй катет D1D* откладываем перпендикулярно первому, его длина равна разнице по высоте между точками Q и D – DZ QD. Гипотенуза прямоугольного треугольника Q1D* идает натуральную величину отрезка QD. С помощью циркуля ставим точку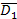 
. На пересечении 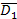H1 и следа плоскости вращения точки С – плоскости g – ставим 
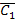. Соединяем точки в треугольник 
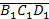. Это и есть натуральный вид DBCD.
РАЗДЕЛ 2 «ИНЖЕНЕРНАЯ ГРАФИКА»
Цели и задачи работы
1) Ознакомление с форматами листов чертежей (ГОСТ 2.301–68*), масштабами изображений (ГОСТ 2.302–68*) и графическим изображением материалов (ГОСТ 2.306–68*).
2) Приобретение навыков вычерчивания разных типов линий на чертежах (ГОСТ 2.303–68*) и написания шрифта (ГОСТ 2.304–81*).
3) Усвоение правил нанесения размеров (ГОСТ 2.307–2011), выполнения изображений (видов, разрезов, сечений) предметов на чертежах (ГОСТ 2.305–2008), построения аксонометрических проекций.
