Рассеяние нейтрона – взаимодействие нейтрона с веществом.
К рассеянию относятся все те взаимодействия нейтрона с ядром, в результате которых образуются нейтрон и ядро, отличающиеся от первоначального только энергией (кинетической или внутренней). Рассеяние бывает двух видов:
- упругое рассеяние (ss) – в результате реакции образуется нейтрон и ядро отдачи с той же внутренней энергией, что и в начальный момент;
- неупругое рассеяние (sin) – в результате реакции образуется нейтрон и ядро отдачи с более высокой внутренней энергией.
Кинематика рассеяния:
Основные соотношения между энергией, которую теряет нейтрон в акте упругого рассеяния, и углом, на который изменяется направление его движения, получаются из законов сохранения энергии и импульса. Соотношение для связи энергии до и после рассеяния имеет вид:
, (6.1)
Где 
, 
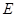- энергии нейтрона соответственно до и после рассеянием;
- масса ядра в атомных единицах;
- косинус угла рассеяния в системе центра инерции.
Связь между косинусами рассеяния в системе центра инерции и лабораторной подчиняется следующему выражению:
, (6.2)
где 
- косинус угла рассеяния в лабораторной системе.
При «лобовом» столкновении 
и потеря энергии максимальна:
, (6.3)
где 
.
Таким образом, максимальная потеря энергии за одно рассеяние:
(6.4)
Заметим, что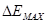 
зависит от энергии до столкновения. В то же время относительная потеря энергии при упругом рассеянии от энергии до столкновения не зависит
(6.5)
Параметр 
зависит только от массы ядра-мишени. Для водорода 
и, следовательно, при лобовом столкновении нейтрона с ядром он теряет всю кинетическую энергию. Энергетический интервал, определяемый выражением (6.4) называется ступенькой замедления. Нейтрон с начальной энергией после столкновения может иметь любую энергию в интервале от до 
. В случае скользящего столкновения 
и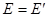 
.
Из соотношения (6.2) следует, что даже, если рассеяние в системе центра масс изотропно, рассеяние в лабораторной системе анизотропно. Легко показать, что средний косинус рассеяния в лабораторной системе в этом случае равен
(6.6)
Из выражения (6.6) следует, что чем легче ядро, тем сильнее анизотропия рассеяния.
Если предположить, что рассеяние сферически симметрично в системе центра инерции, то плотность вероятности нейтрону после рассеяния иметь энергию в интервале от до подчиняется равномерному распределению. Это означает, что энергия нейтрона после рассеяния принимает любое значение из этого интервала с одинаковой вероятностью. Такое рассеяние
, если 
(6.7)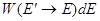 
= 
в остальных случаях
Средняя потеря энергии в одном акте упругого рассеяния равна
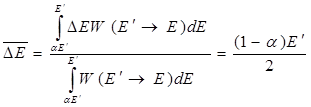. (6.8)
Из (6.8) видно, что доля потерянной энергии зависит только от массы ядра, с которым сталкивается нейтрон.
(6.9)
При изменении энергии от условно принятого начального значения E 0 эВ удобно считать, что текущая энергия E = E 0 exp(- u). Новая переменная u определяется равенством:
. (6.10)
Она получила название летаргии нейтронов. В отличие от энергии летаргия при замедлении нейтронов увеличивается (что и отражено в ее названии), но не в столь больших (по модулю) пределах. Предположим, что при столкновении энергия нейтрона изменилась от E 1 до E 2 < E 1, тогда можно говорить о приращении летаргии 
.
.
Максимальное приращение летаргии при одном ударе будет равно 
= ln(1/a).
Больший интерес представляет, однако, среднее приращение летаргии x при столкновениях нейтронов с энергией E 1 на ядрах с одной и той же массой A.
(6.11)
имеет важный физический смысл, а именно,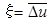 
. Ее называют среднелогарифмическим декрементом энергии рассеянии нейтронов на ядрах массой A. Эта величина уже не зависит от энергии нейтронов до столкновения. Для водорода 
=1, но с увеличением A средняя логарифмическая потеря энергии быстро уменьшается. Уже для A 
3 с хорошей точностью можно пользоваться вместо (6.11) соотношением:
(6.12)
С использованием x легко определить среднее число столкновений, необходимых для изменения энергии с какой-либо начальной энергии E1 до любой конечной E2:
(6.13)
Рис. Рассеяние нейтронов на ядрах вещества. где M, m - масса ядра и масса нейтрона, Еn - начальная энергия
нейтрона, θ - угол между первоначальным направлением движения
нейтрона и направлением движения ядра отдачи в лабораторной
системе координат.
