|

 - скорость изменения функции в точке х.
- скорость изменения функции в точке х.
Пример 1. Пусть функция S=S(t) задает закон прямолинейно движущейся точки. Рассмотрим отношение приращения пути DS к промежутку времени  (приращение пути DS в течении некоторого промежутка времени
(приращение пути DS в течении некоторого промежутка времени  ).
).
|

 - средняя скорость движения точки, чтобы найти мгновенную скорость в конкретный момент времени необходимо
- средняя скорость движения точки, чтобы найти мгновенную скорость в конкретный момент времени необходимо  тогда
тогда  - скорость движения в данный момент. В этом состоит механический смысл производной
- скорость движения в данный момент. В этом состоит механический смысл производной  .
.
Пример 2. Пусть функция q(t)=q – задает закон изменения количества электричества.

2. Геометрический смысл производной.
|

Определение: Касательной к линии L в точке Мо называется предельное положение, которое стремиться занять секущая, если точка М  Мо вдоль L с любой стороны.
Мо вдоль L с любой стороны.
 Рассмотрим функцию y=f(x).
Рассмотрим функцию y=f(x).
Возьмем секущую М0М она образует с осью ОХ угол j из геометрии следует  . Устремим
. Устремим  , а секущая М0М устремится к своему предельному положению – касательной
, а секущая М0М устремится к своему предельному положению – касательной  . Угол
. Угол  устремится к углу a
устремится к углу a


Значения производной в данной точке равны тангенсу угла между положительным направлением оси ОХ и касательной.
Например.
|

3. Дифференцируемость функций.
Определение: Если функция y=f(x) имеет производную в точке х0, т.е. существует предел  то мы говорим, что функция в точке х0 дифференцируема (или, что равносильно, имеет производную).
то мы говорим, что функция в точке х0 дифференцируема (или, что равносильно, имеет производную).
Если функция дифференцируема в некоторой точке промежутка [a,b] или интервала (a, b) то говорят, что она дифференцируема на промежутке [a,b] или интервале (a,b).
Теорема. Если функция y=f(x) имеет конечную производную в точке х0 то функция в точке х0 – непрерывна.
Доказательство: Т.к. 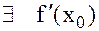 то
то  . Тогда по теореме о пределе, функция имеющая конечный предел будет отличаться от своего предела на б.м. величину
. Тогда по теореме о пределе, функция имеющая конечный предел будет отличаться от своего предела на б.м. величину  приведем к общему знаменателю
приведем к общему знаменателю  отсюда следует, что при
отсюда следует, что при  и
и  , а это означает что функция непрерывна
, а это означает что функция непрерывна  .
.
Таким образом, в точках разрыва функция не может иметь производной.
Тогда возникает вопрос: всякая ли непрерывная функция имеет производную, а вместе с ней и касательную?
Для этого введем понятие односторонних производных.
4. Односторонние производные.
Определение:  - производной в точке х0 слева.
- производной в точке х0 слева.
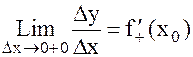 - производной в точке х0 справа.
- производной в точке х0 справа.
Определение: Функция y=f(x) в х0 будет иметь производную когда
 это же условие является условием существование касательной в точке х0.
это же условие является условием существование касательной в точке х0.
Если  - график функции в точке х0 не будет иметь касательной.
- график функции в точке х0 не будет иметь касательной.
Пример 1. Найти производные
 найдем
найдем 


т.к.  в точке х0=1 производной нет,
в точке х0=1 производной нет,
касательной нет.
Не существует производная, не существует касательная.
Пример 2: Найти производную  . Решение:
. Решение:
|
|

5. Бесконечные производные.
Если 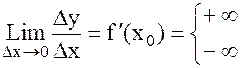 то это несобственное число так же называется производной. Если
то это несобственное число так же называется производной. Если  то такая производная называется односторонней бесконечной производной.
то такая производная называется односторонней бесконечной производной.
Что происходит с касательной?

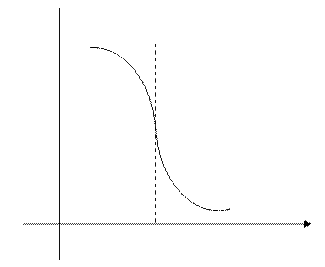
 . Пусть обе односторонние производные совпадают по знаку. Касательная перпендикулярна ОХ и
. Пусть обе односторонние производные совпадают по знаку. Касательная перпендикулярна ОХ и  тогда
тогда
 .
.
Пусть односторонние бесконечные производные разнятся знаками.
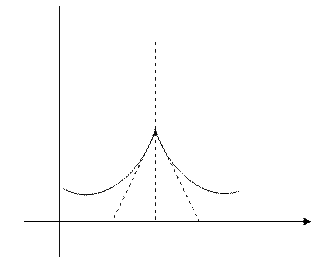

касательная и в этом случае перпендикулярная оси ОХ.
Вывод: Не всякая непрерывная функция в точке непрерывности имеет производную. Класс дифференцируемых функций образует подмножество непрерывных функций.
6. Нахождение производных основных элементарных функций.
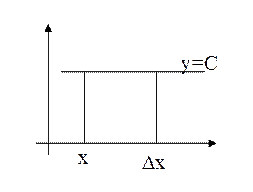
Теорема 1. Производная постоянной равна нулю. Если.  =С, то
=С, то  =0
=0
Доказательство: Найдем приращение функции 

|
Теорема 2: Производная функции  , равна
, равна  .
.
Доказательство: Пусть х получит приращение Dх, тогда  . Для n – целого положительного воспользуемся формулой бинома Ньютона
. Для n – целого положительного воспользуемся формулой бинома Ньютона
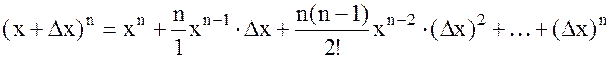
тогда


Замечание: Эта формула справедлива для любого n.
Теорема 3. Производная функции 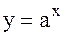 равна
равна  .
.
Доказательство: 
Теорема4. Производная функции  равна
равна  . Доказать самостоятельно.
. Доказать самостоятельно.
Теорема5. Производная  равна
равна 
Доказательство:



Теорема 6: Производная 
Доказательство: аналогично, доказать самостоятельно.
Теорема 7: Производная 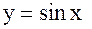 равна
равна  .
.
Доказательство: Найдем приращение 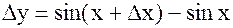 .
.


Теорема 8. Доказать самостоятельно 
Теорема 9. Доказать самостоятельно 
Теорема 10. Доказать самостоятельно 





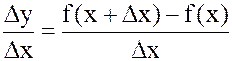 - средняя скорость изменения функции
- средняя скорость изменения функции  на промежутке [x, x+Dx]. Предельный переход при
на промежутке [x, x+Dx]. Предельный переход при  дает скорость изменения функции в самой точке х.
дает скорость изменения функции в самой точке х.
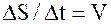 средняя.
средняя.
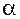 1 - острый, следовательно, tg
1 - острый, следовательно, tg  >0
>0 
 <0
<0 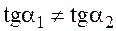 , то производной в т. х0 нет, и касательной нет, касательная есть только одностороння. Такая точка называется угловой.
, то производной в т. х0 нет, и касательной нет, касательная есть только одностороння. Такая точка называется угловой.



