Вход
Модули ОСП, ОТН; математический анализ, алгебра.
Выход
Понятия
Множество
 |
Отношение Подмножество
 |  | ||
Бинарное отношение в X U Y Конечное м. Бесконечное м.
 |
Бинарное отношение в X Счетное м. Континуальное м.
 |
Отношение ОЧП
эквивалентности
ОЛП
Отношение ОЛП
равномощности по мощности
 |
Класс Фактор- Разбиение
эквивалентности множество множества
Мощность
 |
Конечная Счетная Мощность
мощность мощность континуума
| Параметры. | Понятие, обозначение | Определяющее понятие и видовые признаки |
| X Î ObS, < X, ~>, xÎX | Класс эквивалентности элем-та x, [ x ] | Подмножество{yÎX | y~x} Í X |
| X Î ObS, < X, ~> | Фактор - множество, X|~ | ПодмножествоX|~ Í Ã(X), элементами которого являются различные классы эквивалентности элементов м. Xи только они |
| Xa, X, AÎObS Xa Í X "aÎA | Разбиение м. X, X = ëû Xa aÎA | Подмножество {Xa} Í Ã(X) | X = È Xa aÎA & Xa ÇXb = Æ при a ¹ b |
| ObS - с. всех множеств | Отношение равномощности, [ X ] = [ Y ] | Отношение эквивалентности в ObS: X ~ Y: = $ биекция ¦: X «Y |
| X ÎObS | Мощность м. X, [ X ] | Класс эквивалентности м. X по отношению равномощности |
| n Î N | Конечная мощность | Мощность [{1,2, …, n}] |
| Конечное м. | Множествоконечной мощности | |
| Бесконечное м. | Множество, которое не является конечным | |
| Счетная мощность, w | Мощность [N] | |
| Счетное м. | Множество счетной мощности | |
| Мощность континуума, c. | Мощность [ [0,1] ] | |
| Континуальное м. | Множество мощности континуума | |
| X, Y Î ObS | ОЛП по мощности множеств, [ X ] £ [ Y ]. | Отношение линейного порядка в ObS: [ X ] £ [ Y ]: = X равномощно подмножеству Y*ÍY |
Утверждения
УТВ ОЭ-1 О фактор-множестве. Пусть XÎ ObS. Тогда:
(~ - о. эквивалентности в X) Þ X = ëû [ x ].
[ x ] Î X|~
Фактор-множество X| ~ образует разбиение м. X на классы эквивалентности
УТВ ОЭ-2 Об отношении равномощности
Отношение равномощности м. является о. эквивалентности в ObS
УТВ ОЭ-3 Свойства счетных множеств
3.1 Множество Z целых чисел счетно
3.2 Множество рациональных чисел Q счетно
3.3 Всякое подмножество счетного множества не более чем счетно
3.4 Пусть a Î A Î ObS; Xa Î ObS "a Î A. Тогда:
([Xa] = w "aÎ A & [A] £ w) Þ [ È Xa ] = w
aÎA
Конечное или счетное обьединение счетных множеств счетно
3.5 Пусть XÎ ObS. Тогда:
X - бесконечное м. Þ $ X*Í X½ [ X* ] = w
В бесконечном множестве существует счетное подмножество
УТВ ОЭ-4 Свойства континуальных множеств
4.1 Пусть a,b Î R & a < b. Тогда:
[ [0, 1] ] = [ [a,b] ] = [(a,b)] = [ R ] = [ R n] = [ С [ a,b] ] = c
4.2 Пусть [ N ] = w & [[0,1]] =с. Тогда с > w
Мощность континуума строго больше счетной мощности
УТВ ОЭ-5 О сравнении мощностей Пусть ObS - система всех множеств.
Тогда: ([ X] £ [ Y]: = Xравномощно Y*Í Y) Þ < ObS, £ > - ЛУМ
Все множества сравнимы по мощности
УТВ ОЭ-6 Гипотеза континуума
" XÎ ObS: [ X] £ w Ú c £ [ X ]
Не существует множеств мощности больше счетной, но меньше континуальной
УТВ ОЭ-7 Теорема Кантора о мощности множества всех подмножеств
Пусть XÎ ObS. Тогда:
Ã(X) = {X*½X*ÍX} Þ [Ã(X)] > [X]
Мощность множества всех подмножеств м. X строго больше мощности X
УТВ ОЭ-8 Теорема о квадрате. Если Х – бесконечное м., то [X2] = [X].
Умения
УМ ОЭ-1 Дано ~ - отношение эквивалентности в X. Построить фактор-множество X| ~:
1.1 Изобразить (визуализировать) фактор-множество, используя любые способы визуализации множества X(или X2 )
1.2 Выделить класс эквивалентности [ x о ], содержащий фиксированный элемент x о Î X.
УМ ОЭ-2 Пусть XÎ ObS. Определить мощность [ X].
Примеры
ПР ОЭ-1 Пусть X = R 2; <x1, y1> ~ <x2, y2>: = x12 + y12 = x22 + y22; x0 = <0,1>.
Построить фактор-множество X| ~.
 |  | ||
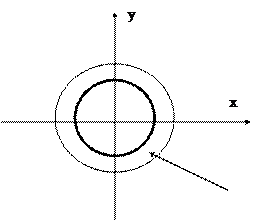[<0,1>]
 |
ПР ОЭ-2. Пусть X= (0, 1). Определить мощность [ X].
Решение. (0,1) Í [0,1] & [ 0.4, 0.5 ] Í (0,1) =([[ a, b ]] = c " a, b Î R ½ a < b)Þ [(0,1)] £ c & c £ [(0,1)] =(антисимметричность £ по мощности м.)Þ [(0,1)] = c ©
Доказательства теорем
УТВ ОЭ 4.2 Пусть [ N ] = w & [[0,1]] = с. Тогда w < с.
Д-во. От противного. Предположим [[0,1]] = w Ü(определение равномощности)Þ $ биекция f: N «[0,1] =(f – сюръекция, в частности)Þ f(N) = {f(k) | kÎ N } = [0,1] (*). Обозначив для "k f(k) = 
Î [0,1], рассмотрим число x = 0,x1x2…xk… Î[0,1], определенное по правилу:
цифра xk = 
, kÎ N
=(определение x)Þ f(k) ¹ x " kÎ N =(xÎ[0,1] & xÏf(N))Þ xÎ[0,1] \ f(N) – противоречит равенству (*). Полученное противоречие доказывает теорему §
Задачи для самостоятельной работы
1. Пусть X,Y Î ObS. Доказать утверждение.
Варианты
1. XÍY Þ [X] £ [Y].
2. Отношение равномощности является отношением эквивалентности.
3. [ Z ] = w.
4. [[a,b]] = с (a<b).
5. [(a,b)] = с (a<b).
6. [ R ] = с.
7. [D] = с.
2. Решите "свой" вариант теста (не забудьте указать вариант, например, ТЕСТ ОЭ - 1). Тестовое задание (ТЗ) с номером № студента (mod12) представьте с решением, на остальные ТЗ пришлите только ответы.
Варианты
1. ТЕСТ ОЭ-1
| № | А | В | Дополнительная информация | |
| Класс эквивалентности элем-та x, [ x ] | Фактор - множество, X|~ | Понятия, < X, ~> | ||
| Конечное м. | Конечная мощность | Понятия | ||
| Счетная мощность, w | Мощность [N] | Понятия | ||
| Рефлексивное, транзитивное, симметричное отношение | ОЛП по мощности множеств, [ X ] £ [ Y ]. | Понятия | ||
| {1,2,3} | Ã({1,2}) | Мощность м. | ||
| [0,1] | Ã([0,1]) | Мощность м. | ||
| Ã({1,2,3}) | {1,2,3,4,5,6,7} | Мощность м. | ||
| x Î [x] | [x] Í X | Пар. высказывания, < X, ~>, x,y,zÎX | ||
| XÍY | [X] £ [Y] | Пар. высказывания, X,YÎObS | ||
| Фактор-м. - м. прямых {y = - x + c| cÎR} | Фактор-м. - м. прямых {x = y + c} | Высказывания, <x1,y1>~<x2,y2> Û x1 - y1 = x2 - y2 | ||
| Фактор-м. - м. прямых {y = c| cÎR} | Фактор-м. - м. прямых {x = c} | Высказывания, <x1,y1>~<x2,y2> Û x1 = x2 | ||
| Класс эквивалентности [<1,1>] = {<x,y>| x = 1} | Класс эквивалентности [<1,1>] = {<x,y>| y = 1} | Высказывания, <x1,y1>~<x2,y2> Û x1 = x2 | ||
2. ТЕСТ ОЭ-2
| № | А | В | Дополнительная информация | |||
| ПодмножествоX|~ Í Ã(X), элементами которого являются различные классы эквивалентности элементов м. Xи только они | Фактор - множество, X|~ | Понятия, < X, ~> | ||||
| Мощность [{1,2, …, n}] | Мощность м. X, [ X ] | Понятия | ||||
| Счетная мощность, w | Счетное м. | Понятия | ||||
| Отношение линейного порядка в ObS [X]£[Y]: = X равномощно подмножеству Y*ÍY | ОЛП по мощности множеств, [ X ] £ [ Y ]. | Понятия | ||||
| N | Q | Мощность м. | ||||
| [0,1] | Rn | Мощность м. | ||||
| Æ | {1} | Мощность м. | ||||
| [x]Ç[y]¹Æ | [x] = [y] | Пар. высказывания, < X, ~>, x,y,zÎX | ||||
| $ биекция 1X :X«Y* = X Í Y | [X] £ [Y] | Пар. высказывания, X,YÎObS | ||||
| Фактор-м. - м. парабол {x = - y2 + c} | Фактор-м. - м. парабол {y = - x2 + c} | Высказывания, <x1,y1>~<x2,y2> Û x1 + y12 = x2 + y22 | ||||
| Фактор-м. - м. прямых {x = c| cÎR} | Фактор-м. - м. прямых {y = c} | Высказывания, <x1,y1>~<x2,y2> Û y1 = y2 | ||||
| Класс эквивалентности [<1,1>] = {<x,y>| x = 1} | Класс эквивалентности [<1,1>] = {<x,y>| y = 1} | Высказывания, <x1,y1>~<x2,y2> Û y1 = y2 | ||||
3. ТЕСТ ОЭ-3
| № | А | В | Дополнительная информация | |
| Разбиение м. X, X = ëû Xa aÎA | Подмножество {Xa} Í Ã(X) | X = È Xa aÎA & Xa ÇXb = Æ при a ¹ b | Понятия, < X, ~> | ||
| Класс эквивалентности м. X по отношению равномощности | Класс эквивалентности элем-та x, [ x ] | Понятия | ||
| Множество счетной мощности | Счетное м. | Понятия | ||
| Множество мощности континуума | Счетное м. | Понятия | ||
| R | Z | Мощность м. | ||
| [0,1]´[0,3] | [-1,1]´[-3,3] | Мощность м. | ||
| R2 | Z3 | Мощность м. | ||
| z ~ x & z ~ y | x ~ y | Пар. высказывания, < X, ~>, x,y,zÎX | ||
| Фактор-м. - м. парабол {x = - y2 + c} | Фактор-м. - м. парабол {y = - x2 + c} | Высказывания, <x1,y1>~<x2,y2> Û x1 + y12 = x2 + y22 | ||
| Фактор-м. - м. прямых {y = c| cÎR} | Фактор-м. - м. прямых {x = c} | Высказывания, <x1,y1>~<x2,y2> Û x1 = x2 | ||
| Класс эквивалентности [<1,1>] = {<x,y>| x = - y2+2} | Класс эквивалентности [<1,1>] = {<x,y> | x = - y2 + 1} | Высказывания, <x1,y1>~<x2,y2>Ûx1+y12=x2 + y22 | ||
| Класс эквивалентности [<1,1>] = {<x,y>| x = 1} | Класс эквивалентности [<1,1>] = {<x,y>| y = 1} | Высказывания, <x1,y1>~<x2,y2> Û x1 = x2 | ||
4. ТЕСТ ОЭ-4
| № | А | В | Дополнительная информация | |
| Отношение эквивалентности в ObS: X ~ Y: = $ биекция ¦: X «Y | Рефлексивное, транзитивное отношение | Понятия | ||
| Счетное м. | Бесконечное м. | Понятия | ||
| Множество мощности континуума | Мощность континуума, c | Понятия | ||
| Мощность [N] | Мощность [ [0,1] ] | Понятия | ||
| [0, + ¥) | [0,1] | Мощность м. | ||
| [0,1]´{0, 3} | {0, 1}´{0, 3} | Мощность м. | ||
| [0,1]´{1,2} | Ã({1,2,3}) | Мощность м. | ||
| [x] Í [y] | x ~ y | Пар. высказывания, < X, ~>, x,y,zÎX | ||
| Фактор-м. - м. прямых {y = - x + c| cÎR} | Фактор-м. - м. прямых {x = y + c} | Высказывания, <x1,y1>~<x2,y2> Û x1 - y1 = x2 - y2 | ||
| Фактор-м. - м. прямых {x = c| cÎR} | Фактор-м. - м. прямых {y = c} | Высказывания, <x1,y1>~<x2,y2> Û y1 = y2 | ||
| Класс эквивалентности [<1,2>] = {<x,y>| y = - x + 1} | Класс эквивалентности [<1,2>] = {<x,y>| x = y - 1} | Высказывания, <x1,y1>~<x2,y2> Û x1 - y1 = x2 - y2 | ||
| Класс эквивалентности [<1,1>] = {<x,y>| x = 1} | Класс эквивалентности [<1,1>] = {<x,y>| y = 1} | Высказывания, <x1,y1>~<x2,y2> Û y1 = y2 | ||
ã Калмыков А.А. 2005. m_oe.doc
