Модуль О Отображение
Вход
Модули ОСП, ОТН
Выход
Понятия
Отображение (о.)
 |
Тождественное о. Композиция о. Обратное о. Обратимое о.
 |
Инъективное о. Сюръективное о. Биективное о.
 |
Сужение о. Продолжение о.
 |
Оператор (о.) Функционал (ф.) Функция
 |  |
О. умножения Интегральный о. Интегральный ф. d - функция
Дирака
Множество
 |
S(X,Y) Подмножество
 | |||
 | |||
Функциональное пространство
 | |||
 | |||
S(T, R) S(T, P)
 |
S[a, b] l B[a, b] C[a,b] Ck[a,b] С∞ [a,b]
 |
L1[a,b] Lp [a,b] l∞ lp l1
Элемент множества
Параметрическое высказывание Оператор
 |  |
Уравнение Оператор Правая часть Решение
уравнения уравнения уравнения
| Параметры | Понятие, обозначение | Определяющее понятиеи видовые свойства |
| X Î ObS | Тождественное о., I (Ix) | ОтображениеI(x) = x:X®X |
| AÎ S(X,Y), BÎ S(Y,Z) | Композиция отображений А и В, ВА | ОтображениеВА(х) = В(А(х)):X®Z |
| AÎ S(X,Y) | Обратное о., А-1 | ОтображениеA -1Î S(Y,X) ú A А-1 = Iy & А-1A = Ix |
| AÎ S(X,Y) | Обратимое о. | ОтображениеА, для которого существует обратное о. |
| AÎ S(X,Y) | Инъективное о. | ОтображениеА: x1 ¹ x2 Þ Ax1 ¹ Ax2 |
| AÎ S(X,Y) | Сюръективное о. | ОтображениеА: A(X) = Y |
| AÎ S(X,Y) | Биективное о. | ОтображениеA, которое одновременно инъективно и сюръективно |
| AÎ S(X,Y), U Í X | Сужение о. А на подмножество U, Aú U | ОтображениеAú U Î S(U,Y): Aú U(x) = A(x) " x Î U |
| AÎ S(X,Y), X Í U | Продолжение о. А на надмножество U, Aú U | ОтображениеAú U Î S(U,Y): Aú U(x) = A(x) " x Î X |
| AÎ S(X,Y) | Оператор (о.) | ОтображениеА, для которого X и Y - ф. п. |
| AÎ S(X,P) | Функционал | ОтображениеА, для которого X - функциональное пространство, а Р- числовое поле |
| XÎObS | Функция | ОтображениеAÎ S(X,R) |
| X=Y= C[a,b] aÎX | О. умножения, Аа | ОператорA аÎ S(X): (Ааx) (t) = a(t) x(t) |
| k Î S([c,d]´ [a,b]) | Интегральный оператор | Оператор(Ax)(t) =  , t Î [c,d]
|
| Дифференциальный о. | ОператорAx = dx/dt | |
| f Î S[a,b] | Интегральный функционал | ФункционалFx =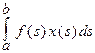 
|
| d - функция Дирака | ФункционалFx = x(0) | |
| X, YÎ ObS | Функциональное пространство (ф.п.) | Подмножествов S(X,Y) |
| a,b Î R | Ф.п. ограниченных на отрезке функций, B[a,b] | Ф. п. Í S[a,b], состоящее из всех ограниченных функций x:[a,b]®P |
| a,b Î R | Ф.п. непрерывных на отрезке функций, С[a,b] | Ф. п. Í S[a,b], состоящее из всех непрерывных функций x:[a,b]®P |
| a,b Î R | Ф.п. k раз непрерывно дифференцируемых на отрезке функций, Сk[a,b] | Ф. п. ÍS[a,b], состоящее из всех k раз непрерывно дифференцируемых функций x:[a,b]®P |
| a,b Î R | Ф.п. бесконечно дифференцируемых на отрезке функций, С∞ [a,b] | Ф. п. Í S[a,b], состоящее из всех бесконечно дифференцируемых функций функций x:[a,b]®P |
| Ф.п. суммируемых последовательностей, l1 | Ф. п. Íl, состоящее из всех суммируемых последовательностей (т.е. таких x = {xk }Î l, что  )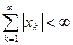
| |
| p³1 | Ф.п. суммируемых в p-й степени последовательностей, lp | Ф. п. Íl, состоящее из всех последовательностей с суммируемой p-й степенью (т.е. таких x = {xk}Î l, что  )
|
| Ф.п. ограниченных последовательностей, l¥ | Ф. п. Íl, состоящее из всех ограниченных последовательностей (т.е. таких x = {xk }Î l, что sup{|xk|: kÎN} < ¥) | |
| a,b Î R | Ф.п. суммируемых на отрезке функций, L1[a,b] | Ф. п. ÍS[a,b], состоящее из всех суммируемых функций x:[a,b]®P (т.е.  ¥)
|
| a,b Î R | Ф.п. суммируемых в p-й степени на отрезке функций, Lp[a,b] | Ф. п. ÍS[a,b], состоящее из всех суммируемых в p-й степени функций x:[a,b]®P (т.е. таких x, что  )
|
| X,Y Î ObS AÎ S(X,Y) = - равенство в Y x Î X, y Î Y | Уравнение, Ax = y | Параметрическое высказывание Ax = y |
| Ax = y - уравнение | Оператор уравнения | ОператорAÎ S(X,Y) |
| Ax = y - уравнение | Правая часть уравнения | Элементy Î Y |
| Ax = y - уравнение | Решение уравнения | Элементx Î X, при котором высказывание Ах = у истинно (т.е. <Ax, y> Î =) |
Утверждения
УТВ О - 1 Свойства композиции отображений
1.1Композиция ассоциативна: (АВ)С = А(ВС)
1.2 Композиция, вообще говоря, не коммутативна
1.3 Композиция сюръективных отображений сюръективна
1.4 Композиция инъективных отображений инъективна
1.5 Композиция биективных отображений биективна
УТВ О - 2 Свойства обратного отображения
2.1 Обратимость отображения эквивалентна его биективности
2.2 Отображение, обратное к данному, единственно
2.3 Композиция обратимых отображений обратима и (ВА)-1 = А-1 В -1
УТВ О - 3 Вложения функциональных пространств
3.1. S[a, b] É B[a, b] É C[a,b] É Ck[a,b] É С∞ [a,b]
3.2. 1 < p < q Þ l1 Ì lp Ì lq Ì l∞ Ì l
3.3. 1 < p < q Þ S[a, b] É L1[a,b] É Lp [a,b] É Lq [a,b]
УТВ О-4 Связь свойств оператора уравнения с разрешимостью уравнения
Пусть Ax = y -уравнение. Тогда:
4.1. А инъективен Û Уравнение Ax = y не может иметь более одного решения" y ÎY
4.2. А сюръективен Û Уравнение Ax = y имеет решение при " y ÎY
4.3 А биективен Û Уравнение Ax = y при " y ÎY имеет единственное решение, которое может быть найдено по формуле x = A-1y, где A-1 - обратный оператор
Умения
УМ О-1 Даны о. А и аргумент х. Найти значение Ах.
УМ О-2 Даны два (несколько) отображения. Найти значение композиции отображений на данном аргументе.
УМ О-3 Дано отображение А. Найти условие обратимости А и найти A-1 .
УМ О-4 Дано ф. п. Х и элемент х. Определить истинность высказывания x Î Х
УМ О-5 Дано уравнение Аx = y. Найти условия разрешимости уравнения, пользуясь УТВ О-4.
Примеры
ПР О-1 Дано: А: С[0,1] ®C[0,1],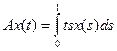 
, t Î [0,1], x (t) = t. Найти значение Ах.
Решение. А x (t) = 
ПР О-2 Даны: X = C[0,1], A: X ® X, 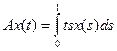, t Î [0,1], B x(t) = tx(t): X®X,
F x = x(1): X® R, x (t) = t. Найти FAB x и FBA x.
Решение. 1. B x (t) = t2; AB x (t) =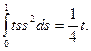 
FAB x = 1/4. Аналогично: FBA x = 1/3.
ПР О-3 Дано: Аa: С[0,1] ®C[0,1], a Î С[0,1]. Найти необходимое и достаточное условие обратимости Аa и найти Аa-1.
Решение. Решим уравнение Аa x = y: ax = y Û x = (1/a)y (a (t) > 0 " t или a (t) < 0 " t - необходимое и достаточное условие обратимости Аa) Û Аa-1 = A1/a.
ПР О-4 Дано X = l2 , x = {xk = 
}. Определить истинность высказывания xÎ l2 .
Решение. 
Þ высказывание xÎ l2 ложно.
ПР О-5. Дано уравнение Аx = y. Найти условия разрешимости уравнения, пользуясь УТВ О 4. Пусть X=Y= l 1; A:X®X; Ax = {0,x1,x2,…}.
Решение. 1. Если x = {x1,x2,x3,…}Î l 1, то y = {1,x2,x3,…}Î l 1 \ imA Ü(определение сюръективного о.)Þ А не является сюръективным о. Ü(УТВ О-4.2)Þ $ правая часть yÎY, для которой уравнение Аx = y не имеет решения. ImA = {yÎ l 1 | y1 = 0}=(определение образа о., imA)Þ для "правой части yÎimA уравнение Аx = y имеет решение, т.е. условие разрешимости: y1 = 0.
2. Если x = {x1,x2,x3,…}¹ y = {y1,y2,y3,…}=(покоординатное равенстово в пространстве l 1)Þ Ax = {0,x1,x2,…} ¹ Ay = {0,y1,y2,…}=(определение инъектитвного о.)Þ А инъективное о.
Ü(УТВ О-4.1)Þ уравнение Ax = y не может иметь более одного решения " y ÎY ¨
