Случайная величина Х может принять значение х1 с вероятностью Р1, значение х2 с вероятностью Р2, …, значение хn с вероятностью Рn. Схематично это показано на рис. 8.
Для моделирования такой случайной величины можно воспользоваться датчиком случайной величины E с равномерным распределением в интервале от 0 до 1. Выданное датчиком значение е последовательно сравнивается следующим образом:
если е < P(
), то принимаем Х = ,
если е < P(
) + P(), то принимаем Х = ,
……
если е < P() + P()+ … +P(
), то принимаем Х = ,
если ни одно из предыдущих условий не выполнено, то принимаем Х=хn.
10) Универсальным методом моделирования непрерывных случайных величин является метод исключения. При моделировании случайной величины Х с плотностью распределения вероятности в интервале от a до b используется следующий алгоритм:
1. Получение от датчика случайных чисел с равномерной плотностью распределения вероятности в интервале от 0 до 1 двух независимых значений случайных величин: 
и 
.
2. Расчет = а + (b - а) , = f max , где f max - максимальное значение f(х).
3. Если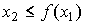 
, то представляет моделируемое значение случайной величины. Если данное неравенство не выполняется, то возвращаемся к пункту 1.
Метод обратной функции
Пусть непрерывная случайная величина (СВН) 
задана своим законом распределения:
, где 
– плотность распределения вероятностей, а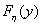 
- функция распределения вероятностей. Доказано, что случайная величина
распределена равномерно на интервале (0,1).
Отсюда следует, что искомое значение y может быть определено из уравнения:
(5)
которое эквивалентно уравнению:
где y – значение случайной величины 
. Решение уравнения (6) можно записать в общем виде через обратную функцию 
Основной недостаток метода заключается в том, что интеграл (5) не всегда является берущимся, а уравнение (6) не всегда решается аналитическими методами.
12) Метод сверток.
Выразить искомую случ. величину в виде суммы других случ. величин, для которых легко получить реализацию гамма-распределения.(и хер знает, что это за буквы в формуле)
 |
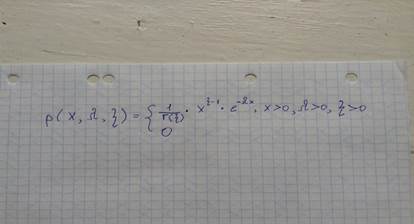13. Моделирование равномерно распределенных случайных величин.
Особое значение в статистическом моделировании имеет непрерывная равномерно распределенная случайная величина. Особая значимость этой случайной величины объясняется тем, что, во-первых, она сама по себе необходима для моделирования случайных процессов и величин и, во-вторых, случайные величины с другими законами распределения формируются на их основе.
Определение. Непрерывная случайная величина 
имеет равномерное распределение в интервале 
где a<b, если ее плотность вероятности 
определяется так:
Значения характеристик равномерного закона распределения:
- математическое ожидание;
- дисперсия.
При моделировании часто используются случайные числа из интервала 
. Непрерывная случайная величина равномерно распределена в интервале , если:
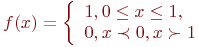
В этом случае 
.
В Exel: =слчис(); (Є [0;1)
=целое(а+(в-а)*слчис());(Є [а;в)
14. Моделирование случайных величин, имеющих экспоненциальное распределение.
Говорят, что случайная величина X имеет показательное (экспоненциальное) распределение с параметром λ > 0, если она непрерывна, принимает только положительные значения, и имеет плотность распределения
Функция распределения 
Математическое ожидание 1 / λ
Дисперсия 1 / λ2
|
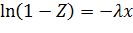
Экспоненциальное распределение используется в теории вероятности и в теории массового обслуживания. Для моделирования времени, периода заявок в СМО.Этот закон распределения нам часто встречается в приложениях, особенно в радиотехнических и коммуникационных. В частности, часто предполагается, что время разговора двух абонентов распределено по показательному закону.
«+»- простой
«-» - непременим для моделирования многих важных распределений
15.Моделирование нормально распределенной случайной величины.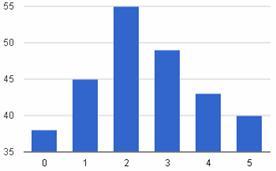 
Это самое популярное из стандартных распределений вероятности, и на первый взгляд может показаться странным, что наиболее распространена такая сложная формула.
Случайная величина распределена нормально или по Гауссу, если
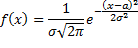
Плотность распределения
Математическое ожидание такой случайной величины равно a, а дисперсия — σ2.
16.Моделирование случайных величин, распределенных по закону Пуассона.
описывает число событий, происходящих в одинаковых промежутках времени при условии, что события происходят независимо одно от другого с постоянной интенсивностью.
При рассмотрении маловероятных событий, имеющих место в большой серии независимых испытаний некоторое (конечное) число раз, вероятности появления этих событий подчиняются закону Пуассона или закону редких событий 
, где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, x -частота данного события.
Математическое ожидание такой случайной величины равно λ, и дисперсия тоже λ.
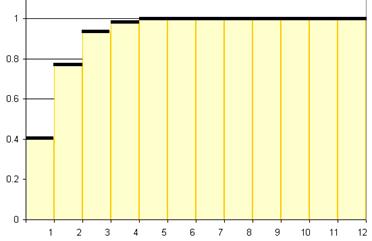
Пуассоновское распределение характерно для схемы редких событий — в которой складывается очень много случайных величин с распределением Бернулли (случайная величина распределена по Бернулли, если она принимает всего два значения, обычно этими значениями являются 1, вероятность которой равна p, и 0, вероятность которого равна q = 1 − p) и очень малой вероятностью положительного исхода у каждого.
Например, отмечалось, что количество писем, опущенных в почтовый ящик с ненадписанным конвертом, имеет пуассоновское распределение.
17.Дискретные имитационные модели. Примеры.
Дискретное имитационное моделирование. Элементы дискретных систем, такие как люди, оборудование, заказы и т.п., включенные в имитационную модель, называют ее компонентами. Каждый компонент описывается различными характеристиками (атрибутами). Компоненты, участвующие в действиях различного типа, могут иметь одну или несколько общих характеристик, что позволяет объединять их в группы. Группы компонентов называются файлами. Включение компонента в файл означает, что он логически связан с другими компонентами этого файла.
Целью дискретного имитационного моделирования является воспроизведение взаимодействий, в которых участвуют компоненты, и изучение поведения и функциональных возможностей исследуемой системы. Для этого выделяются состояния системы и описываются действия, которые переводят ее из одного состояния в другое. Говорят, что система находится в определенном состоянии, когда все ее компоненты находятся в состояниях, совместимых с областью значений, описывающих это состояние характеристик. Таким образом, имитация – это «динамический портрет» состояний системы во времени, т.е. воспроизведение поведения системы во времени.
При дискретной имитации состояние системы может меняться только в моменты совершения событий. Так как состояние системы не изменяется между этими моментами, полный динамический портрет состояний системы может быть получен путем продвижения имитационного времени от одного события к другому.
Функционирование дискретной имитационной модели можно задать одним из следующих способов:
– определяя изменения состояний системы, происходящие в моменты свершения событий;
– описывая действия, в которых принимают участие элементы системы;
– описывая процесс[2], через который проходят элементы.
Эти представления лежат в основе трех альтернативных методологических подходов к построению дискретных имитационных моделей, называемых обычно событийным подходом, подходом сканирования активностей (обозначает подход, ориентированный на действия) и процессно-ориентированным подходом.
Событийный подход. При событийном подходе система моделируется путем идентификации изменений, происходящих в ней в моменты совершения событий. Задача исследователя заключается в описании событий, которые могут изменить состояние системы, и определении логических взаимосвязей между ними. Имитация функционирования системы осуществляется путем выполнения упорядоченной во времени последовательности логически взаимосвязанных событий.
Подход сканирования активностей. При использовании подхода сканирования активностей разработчик модели описывает действия, в которых принимают участие элементы системы, и задает условия, определяющие начало и окончание этих действий. События, которые начинают или завершают действие, не планируются разработчиком модели, а инициируются по условиям, определенным для данного действия. Условия начала или окончания действия проверяются после очередного продвижения имитационного времени. Если заданные условия удовлетворяются, происходит соответствующее действие. Чтобы было выполнено каждое действие в модели, сканирование условий производится для всего множества действий при каждом продвижении имитационного времени.
Подход сканирования активностей наиболее эффективен для ситуаций, в которых продолжительность действия определяется в зависимости от того, насколько состояние системы удовлетворяет заданным условиям. Тем не менее, в силу необходимости сканирования условий для каждого действия, подход сканирования активностей менее эффективен по сравнению с событийным подходом, и поэтому находит ограниченное применение в дискретной имитации.
Процессно-ориентированный подход. Многие имитационные модели содержат последовательности компонентов, которые возникают в них по определенной схеме. Процессно-ориентированный подход, сочетая в себе черты событийного подхода и подхода сканирования активностей, обеспечивает описание прохождения компонентов через процесс, содержащий ресурсы. Простота этого подхода в том, что, как правило, логика событий закладывается в инструментарий разработки имитационной модели. Однако, этот подход является менее гибким, чем событийный. Кроме того, требуется постоянный анализ состояния ресурсов после их использования.
18. Имитационное моделирование систем массового обслуживания
При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО). Каждая СМО состоит из определенного числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые называются каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы и др. По числу каналов СМО подразделяют на одноканальные и многоканальные.
Заявки поступают в СМО обычно не регулярно, а случайно, образуя так называемый случайный поток заявок (требований). Обслуживание заявок также продолжается какое-то случайное время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое количество заявок (они либо становятся в очередь, либо покидают СМО не обслуженными), в другие же периоды СМО работает с недогрузкой или простаивает.
Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоком заявок. В качестве показателей эффективности СМО используются:
– Абсолютная пропускная способность системы (А), т.е. среднее число заявок, обслуживаемых в единицу времени;
– относительная пропускная способность (Q), т.е. средняя доля поступивших заявок, обслуживаемых системой;
– вероятность отказа обслуживания заявки (
);
– среднее число занятых каналов (k);
– среднее число заявок в СМО (
);
– среднее время пребывания заявки в системе (
);
– среднее число заявок в очереди (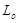
);
– среднее время пребывания заявки в очереди (
);
– среднее число заявок, обслуживаемых в единицу времени;
– среднее время ожидания обслуживания;
– вероятность того, что число заявок в очереди превысит определенное значение и т.п.
СМО делят на 2 основных типа: СМО с отказами и СМО с ожиданием (очередью). В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует (например, заявка на телефонный разговор в момент, когда все каналы заняты, получает отказ и покидает СМО не обслуженной). В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.
Одним из методов расчета показателей эффективности СМО является метод имитационного моделирования. Практическое использование компьютерного имитационного моделирования предполагает построение соответствующей математической модели, учитывающей факторы неопределенности, динамические характеристики и весь комплекс взаимосвязей между элементами изучаемой системы. Имитационное моделирование работы системы начинается с некоторого конкретного начального состояния. Вследствие реализации различных событий случайного характера, модель системы переходит в последующие моменты времени в другие свои возможные состояния. Этот эволюционный процесс продолжается до конечного момента планового периода, т.е. до конечного момента моделирования.
19.Непрерывные имитационные модели. Примеры.
В непрерывной имитационной модели состояние системы представляется с помощью непрерывно изменяющихся зависимых переменных. Непрерывная имитационная модель создается путем задания уравнений для совокупности переменных состояния, динамическое поведение которых имитирует реальную систему.
Модели непрерывных систем часто определяются в терминах производных переменных состояния. Уравнения такого вида, включающие производные переменных состояния, называются дифференциальными уравнениями. Например:
Первое уравнение определяет скорость изменения вектора переменных состояния, а второе уравнение является начальным условием для этого вектора.
Цель имитационного эксперимента – определить значение переменных состояния в зависимости от имитационного времени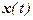 
.
Определение временной зависимости 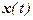на цифровых ЭВМ выполняется с помощью методов численного интегрирования.
Другой способ описания моделей непрерывных систем – использование разностных уравнений. В этом случае временная ось разбивается на временные периоды длиной ∆t. Динамика переменной состояния описывается уравнением, которое позволяет вычислить значение переменной в момент времени k · ∆t на основе ее значения в предыдущий момент времени (k-1) · ∆t. Например:
