Обратная ветвь к.к. Р

Поиск: Рекомендуем:  Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки) Нейроглия (или проще глия, глиальные клетки)
Категории:
|
Относительное изменение коэффициента пористости пропорционально изменению нагрузки (для малых интервалов нагрузок).
Обратная ветвь к.к. Р
| Компрессия – это сжатие грунта без возможного бокового расширения.
 Схематично это можно представить так: Схематично это можно представить так:
            
    ∞
h ∞
h

 σ σ
| |||||||
| Из графика видно, что происходит необратимое уплотнение грунта. Нас интересует в основном только прямая ветвь к.к., обратная ветвь к.к. –возможность поднятия дна, при глубоких котлованах (гидротехническое строительство). | 
       
       b b
|
Изобразим снова компрессионную кривую:
 е е
  е е
 Р Р
| На небольшом участке рассмотрим приращение нагрузки  Р и получим соответств. Р и получим соответств.  е. Заменим дугу прямой и рассмотрим угол е. Заменим дугу прямой и рассмотрим угол  . .
 е = tg е = tg   Р
(-) – с увеличением нагрузки Р
(-) – с увеличением нагрузки  - уменьшается.
В дифференциальной форме: - уменьшается.
В дифференциальной форме:
 de = tg de = tg   Р
tg Р
tg  = mо и тогда de = mо dР - основная математическая форма закона компрессии. = mо и тогда de = mо dР - основная математическая форма закона компрессии.
|
Относительное изменение коэффициента пористости пропорционально изменению нагрузки (для малых интервалов нагрузок).
Р | Компрессионная кривая позволяет судить о сжимаемости грунта.
 - может характеризовать сжимаемость. - может характеризовать сжимаемость.
| |||||||||||||||
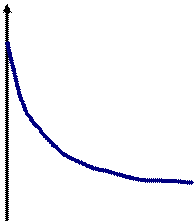
    i i
р1рi р2 Р

| Возьмем произвольную точку i на прямой, в пределах отрезка Р1- Р2. Составим уравнение для этой точки, исходя из начального параметра ео
еi = ео – рi tg  - это основное уравнение, характеризующее компрессию в выбранном варианте.
Рассмотрим подробнее - это основное уравнение, характеризующее компрессию в выбранном варианте.
Рассмотрим подробнее  .
tg .
tg  = mo= = mo=   , ,  mo – коэффициент сжимаемости грунта.
mo – коэффициент сжимаемости грунта.
|
Для того чтобы получить mo, необходимо выделить определенный интервал.
 Р1 – напряжение от собственного веса грунта.
Р1 – напряжение от собственного веса грунта.
Р – дополнительное давление от внешней нагрузки.
Р2 – полное напряжение (Р2 = Р1 + Р)
Окончательно: mo = 
 ,
,  ,
, 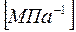
Если:

mo < 0,005 – грунт мало сжимаемый
mo = 0,005  0,05 – грунт средне сжимаемый
0,05 – грунт средне сжимаемый
mo > 0,05  - грунт сильно сжимаемый
- грунт сильно сжимаемый
Итак:
1. При изысканиях отбирают пробы грунта, строят график к.к. и определяют mo – это делают обычно инженеры – геологи, а строители оценивают свойства грунта по показателям, полученным от геологов.
2.
|
 Основной расчёт оснований по II предельному состоянию – по деформациям. В формулу расчёта осадки входит величина - коэффициента относительного сжатия грунта.
Основной расчёт оснований по II предельному состоянию – по деформациям. В формулу расчёта осадки входит величина - коэффициента относительного сжатия грунта.
 |
 S = h mv P – прямо пропорциональная связь.
S = h mv P – прямо пропорциональная связь.
Таким образом mо – является той характеристикой, которая как правило, решает выбор основания - можно строить или нельзя (тогда возникает необходимость перехода на искусственное основание).
В России существует ещё одна характеристика сжатия грунта - Ео – модуль общей деформации грунта.

Ео =  =
=  ( Аналогичен закону Гука, но там используется модуль упругой деформации)
( Аналогичен закону Гука, но там используется модуль упругой деформации)
 Ео – характеризует упругие + остаточные деформации (эти деформации не разделяются, так как в большинстве случаев для здания это не имеет никакого значения).
Ео – характеризует упругие + остаточные деформации (эти деформации не разделяются, так как в большинстве случаев для здания это не имеет никакого значения).

 Ео=
Ео=  , где
, где 
 - коэффициент
- коэффициент
Пуассона (бокового расширения грунта)
 mo (mv)
mo (mv)
 Сжимаемость грунта характеризуется
Сжимаемость грунта характеризуется
Ео
Испытания грунтов пробными статическими нагрузками и определение модуля деформации.
Выполняя отбор проб для испытания грунтов, мы нарушаем его структуру и, следовательно, нарушаем его свойства. Поэтому производят полевые испытание грунта штампами: большого и малого диаметра.

| Стандартный штампа F = 5000 см2 Нагрузка увеличивается ступенями = 0,05 МПа Наблюдаем за осадкой нашего штампа. Так как нагрузку задаем сами, то в любой момент времени знаем Р. Такая задача решена в теории упругости. |
 - формула Шлейхера – Буссинеска
- формула Шлейхера – Буссинеска
 - коэффициент, зависящий от жёсткости штампа.
- коэффициент, зависящий от жёсткости штампа.
b – ширина штампа
 - коэффициент бокового расширения грунта (коэффициент Пуассона)
- коэффициент бокового расширения грунта (коэффициент Пуассона)
Е0 - модуль общей деформации.
Достоинства:
- испытание грунта ненарушенной структуры
Недостатки:
- трудоемкость;
- продолжительность испытаний

|
|
|
|
|
Дата добавления: 2017-01-28; Мы поможем в написании ваших работ!; просмотров: 407 | Нарушение авторских прав
Лучшие изречения: