ЭЛЕМЕНТЫ РАСЧЕТА ЦФ
1. Принципы расчёта рекурсивных ЦФ
Расчёт таких фильтров состоит из двух основных этапов.
1. Получение (расчет) передаточной функции  , которая удовлетворяет требованиям обработки сигнала.
, которая удовлетворяет требованиям обработки сигнала.
2. Создание процедуры перехода, которая преобразует  в соответствующую передаточную функцию
в соответствующую передаточную функцию  цифрового фильтра.
цифрового фильтра.
При проведении 2-го этапа расчета необходимо выполнить два условия.
Условие 1. Мнимая ось 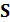 - плоскости
- плоскости  отображается в единичную окружность в
отображается в единичную окружность в 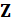 - плоскости.
- плоскости.
Условие 2. Левая половина S-плоскости отображается в 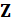 - плоскость внутрь единичного круга
- плоскость внутрь единичного круга 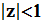 .
.
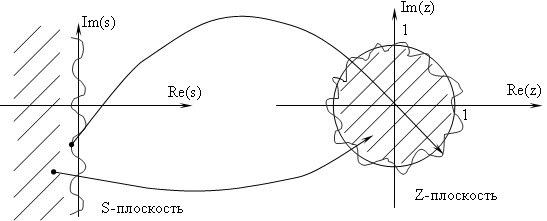
Рисунок 1
Условие 1 необходимо соблюдать для сохранения частотных свойств при переходе от аналогового к цифровому фильтру. Условие 2 – для сохранения устойчивости фильтра.
Метод инвариантного преобразования импульсной характеристики
1. Задается или получается в результате расчётов передаточная функция  аналогового фильтра (фильтра-прототипа), которая удовлетворяет требованиям обработки сигнала.
аналогового фильтра (фильтра-прототипа), которая удовлетворяет требованиям обработки сигнала.
2. По  путем обратного преобразования Лапласа находится импульсная характеристика (ИХ) аналогового фильтра
путем обратного преобразования Лапласа находится импульсная характеристика (ИХ) аналогового фильтра

3. ИХ  подвергается дискретизации и находится ИХ ЦФ
подвергается дискретизации и находится ИХ ЦФ
 .
.
4. По 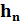 находится системная функция ЦФ:
находится системная функция ЦФ: 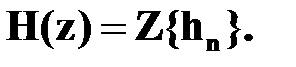
Далее  записывается в форме, удобной для реализации.
записывается в форме, удобной для реализации.
Пример.
1. 
2. 

3. 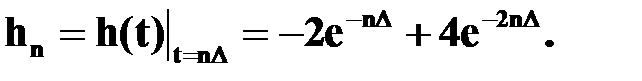
4.  Структурная схема рассчитанного ЦФ будет выглядеть следующим образом:
Структурная схема рассчитанного ЦФ будет выглядеть следующим образом:

Рисунок 2 – Структурная схема ЦФ
Метод билинейного преобразования
Моделирование операции интегрирования
Рассмотрим интеграл
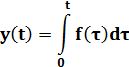
| (1) |
Перейдём к дискретной функции, подставим вместо t величину mD.
Интеграл (1) примет вид  ;
; 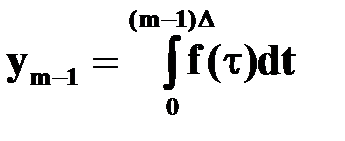 .
.
На основе свойств, определённого интеграла, можно записать:
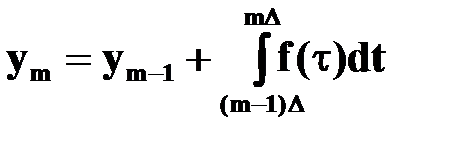 . (2)
. (2)
Получено рекуррентное соотношение, которое позволяет последовательно шаг за шагом вычислять значение интеграла в точках от 0 до  . Конкретный вид соотношения зависит от того, каким образом аппроксимируется интеграл в выражении (2).
. Конкретный вид соотношения зависит от того, каким образом аппроксимируется интеграл в выражении (2).
Рассмотрим способ трапеций:
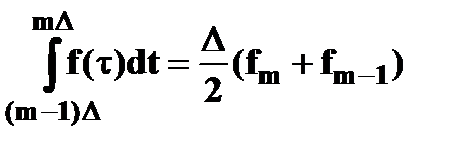 (3)
(3)

Рисунок 3 – Вычисление интеграла на интервале
Подставив последнее выражение в формулу (2), получим:

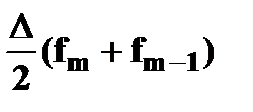 . (4)
. (4)
Осуществим 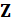 - преобразование полученного разностного уравнения:
- преобразование полученного разностного уравнения:
 .
.
Найдём 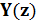 :
:
 . (5)
. (5)
Преобразуем по Лапласу интеграл (1):
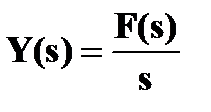 . (6)
. (6)
Сравнивая выражения (5) и (6), делаем вывод, что для моделирования
операции интегрирования необходимо осуществить замены:
 на
на 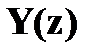 ; 2.
; 2. 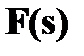 на
на  ; 3.
; 3. 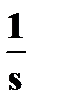 на
на 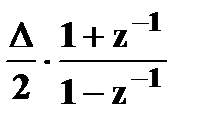 . (7)
. (7)
Такие замены (7) называется билинейным преобразованием.
3.2. Использование билинейного преобразования Использование метода билинейного преобразования заключается в подстановке в передаточную функцию  фильтра-прототипа вместо s
фильтра-прототипа вместо s
выражения 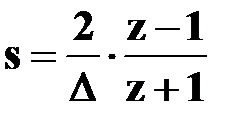 и получении, таким образом,
и получении, таким образом,  :
:
 .
.
Исследуем изменение частотных характеристик при переходе к  , для чего вместо s подставим
, для чего вместо s подставим  , а вместо
, а вместо 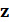 –
– 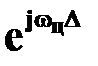 .
.
Получим:

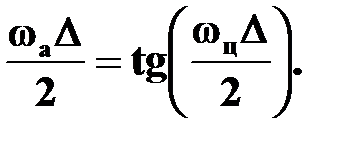 (8)
(8)






