Потенциал и работа сил электрического поля. Основываясь на определении потенциала, можно показать, что работа сил электрического поля при перемещении точечного заряда q из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов в начальной и конечной точках пути, A = q (j1 - j2).
Если по аналогии с потенциальной энергией считать, что в точках, бесконечно удалённых от электрических зарядов - источников поля, потенциал равен нулю, то работу сил электрического поля при перемещении заряда q из точки 1 в бесконечность можно представить как A¥ = q j1.
Таким образом, потенциал â данной точке электростатического поля - это физическая величина, численно равная работе, совершаемой силами электрического поля при перемещении единичного положительного точечного заряда из данной точки поля в бесконечно удаленную: j = A¥ / q.
В некоторых случаях потенциал электрического поля нагляднее определяется как физическая величина, численно равная работе внешних сил против сил электрического поля при перемещении единичного положительного точечного заряда из бесконечности в данную точку. Последнее определение удобно записать следующим образом:
7,8 Связь между энергией и силой Кулона, напряжённостью и потенциалом.
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
Для установления этой связи вычислим элементарную работу ∆A, совершаемую силами поля при малом перемещении ∆S тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой S. Эта работа равна: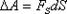 
где 
- проекция силы 
на направление 
.
Поскольку в данном случае работа совершается за счет запаса потенциальной энергии ∆, она равна убыли потенциальной энергии -∆ на отрезке оси ∆S: ∆A = -∆
Из двух последних выражений получаем: 
Откуда: 
Последнее выражение дает среднее значение на отрезке ∆S. Чтобы получить значение в точке нужно произвести предельный переход: 
Так как может изменяться не только при перемещении вдоль оси S, но также и при перемещениях вдоль других направлений, предел в этой формуле представляет собой так называемую частную производную от по S: 
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z: 
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы: 
в математике вектор 
, где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 
. Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком: 
Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал, на близко расположенную эквипотенциальную поверхность, имеющую потенциал 
Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения 
С другой стороны 
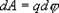. Из этих уравнений получаем 
Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
9 Поток вектора напряжённости электростатического поля. Теорема Гаусса.
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE.
Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным.
Поток напряженности через такую элементарную площадку будет равен по определению.
где 
- угол между силовой линией и нормалью 
к площадке dS; 
- проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен 
Так как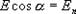 
, то: 
где 
- проекция вектора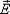 
на нормаль и к поверхности dS.
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0. 
Внешний заряд не создаёт поток.
0 Вычисление напряжённости поля вблизи бесконечной плоскости, нити с поверхностной плотностью заряда σ и линейной плотностью заряда τ.
Расчёт напряжённости бесконечной плоскости
Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS. Применив теорему Гаусса, получим:
из которого 
Расчёт напряжённости бесконечной нити
Рассмотрим поле, создаваемое бесконечной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:
В силу симметрии, модуль напряжённости в любой точке поверхности цилиндра будет одинаков. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:
Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю. Приравнивая 1 и 2 выражения, получим:
