Пример решения типового задания

Задание №1

Дано комплексное число .

1. Записать число в алгебраической, тригонометрической и показательной форме, изобразив его на комплексной плоскости.

2. Вычислить .

Решение:

1. Приведем к алгебраической форме комплексного числа. Для этого умножим числитель и знаменатель дроби на число комплексно сопряженное знаменателю. Получим:

Итак, алгебраическая форма комплексного числа .

Запишем в тригонометрическом виде, используя формулу (1): Имеем: ,

Изобразим на комплексной плоскости:

0 1 х

у

 

Итак, тригонометрическая форма имеет вид:

. В показательной форме: .

2. Вычислим , используя формулу:

Ответ: 1. ;

2.

 

Пример 2.

1. Решить уравнение .

2. Записать корни уравнения и в алгебраической, тригонометрической и показательной форме, изобразив их на комплексной плоскости.

Решение:

1. Найдем корни данного квадратного уравнения по известной формуле

, зная, что .

(Знак используется как квадратный корень из комплексного числа!)

Получим два комплексно сопряженных корня

.

2. Имеем алгебраическую форму и .

Действительная и мнимая часть, соответственно, равны:

Изобразим и на комплексной плоскости:

Запишем числа и в тригонометрической и показательной форме. Имеем: , , ;

y

0 3 x

, ; ;

.

Ответ:

Задание № 2

Вычислить пределы.

Решение.

1. (разложим числитель и знаменатель на множители) ;

2. (разделим числитель и знаменатель на наибольшую степень ; в данном случае на )=

(т.к. функция, обратная бесконечно большой, есть бесконечно малая: );

3. (умножим числитель и знаменатель на )

= ;

4. (применим правило Лопиталя (3)) .

 

Ответ: 1. ; 2. ;

3. ; 4.

Задание №3

Подобрать параметры и так, чтобы функция была непрерывна.

Решение.

Функция составлена из элементарных функций, каждая из которых непрерывна на указанных промежутках. Непрерывность может нарушаться только в точках и .

Вычислим односторонние пределы функции в этих точках.

а) ; ;

.

Условие непрерывности функции в точке 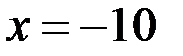записывается в виде .

б) ; ; .

Условие непрерывности функции в точке записывается в виде .

в) Получаем систему линейных уравнений:

.

Решение системы дает значения искомых параметров: .

Ответ:

Задание №4

Продифференцировать данные функции по переменной .

1. ; 2. ; 3. .

Решение.

1.

.

Используем правило дифференцирования сложной функции: если , где функции и имеют производные, то . Полагаем и . Получаем:

.

Тогда

.

2. В этой задаче функция задана параметрически, т.е. уравнениями:

.

Производная находится по формуле: .

Проводим вычисления:

;

.

3. Функция задана неявно уравнением . Для определения нужно продифференцировать функцию по , рассматривая при этом как функцию переменной . Приравнивая полученную производную к нулю, получаем уравнение первой степени относительно . Из этого уравнения и находим производную.

, ,

, ,

.

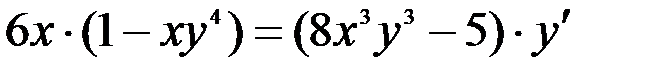
Ответ: 1. ;

2. ; 3. .

Задание №5

Исследовать функцию с помощью производной и построить график.

Решение.

1. Область определения функции: ; ;

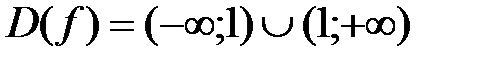
2. Точки пересечения с осями координат.

, так как уравнение не имеет вещественных корней, то график функции не имеет точек пересечения с осью .

, т.е. график пересекает ось в точке (0;–1).

3. Исследование функции на четность (нечетность).

.

Функция не является ни четной, ни нечетной, т.е. – это функция общего вида.

4. Функция непериодическая.

5. Исследование непрерывности. Классификация точек разрыва.

Функция терпит разрыв в точке . Определим тип разрыва:

.

Односторонние пределы функции бесконечны, следовательно, – точка разрыва второго рода (точка бесконечного разрыва).

6. Интервалы монотонности, точки экстремума функции.

Найдем первую производную функции:

, .

–

–

+

+

1

Точки экстремума:

Функция имеет максимум при , так как в при переходе через эту точку производная меняет знак с (+) на (–), причем .

Функция имеет минимум при , так как при переходе через эту точку производная меняет знак с (–) на (+), причем .

Функция возрастает при .

Функция убывает при

7. Интервалы выпуклости и точки перегиба.

Найдем вторую производную функции:

в ноль не обращается, значит, точек перегиба нет.

–

+

○

При направление выпуклости графика вверх (выпуклость), а при – вниз (вогнутость).

8. Асимптоты.

Прямая является вертикальной асимптотой графика функции (см. пункт 5).

Найдем наклонные асимптоты :

;

Итак, график имеет наклонную асимптоту (правую и левую).

9. График функции.

M JEZYS2p39GuJ/U+799mecBQaL4cARSLBJzYcNCX3UErYn6wukkR0pt8ljzXehiJ3xHgcFPk1SnE/ 6NlV8AB8DsDnk9Qa+XeR+JEpH7jUD2LpV6zdz7ju/mz3xR8AAAD//wMAUEsDBBQABgAIAAAAIQAG OQT14AAAAAoBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BS8NAEIXvgv9hGcGb3STaRGM2pRT1VARb Qbxts9MkNDsbstsk/feOJ729xzzefK9YzbYTIw6+daQgXkQgkCpnWqoVfO5f7x5B+KDJ6M4RKrig h1V5fVXo3LiJPnDchVpwCflcK2hC6HMpfdWg1X7heiS+Hd1gdWA71NIMeuJy28kkilJpdUv8odE9 bhqsTruzVfA26Wl9H7+M29Nxc/neL9+/tjEqdXszr59BBJzDXxh+8RkdSmY6uDMZLzr2y5S3BBZp AoIDafaQgTiwSLInkGUh/08ofwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAA AAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAA AJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQDL09+1KwkA AP47AAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQAGOQT1 4AAAAAoBAAAPAAAAAAAAAAAAAAAAAIULAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA kgwAAAAA ">

 

 

-1 0 1 x

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

 

1. Дифференциальное и интегральное исчисления для втузов, т.1 / Н.С. Пискунов– М: Наука, 1985. – 456 с.

2. Конспект лекций по высшей математике, ч.1 / Дмитрий Письменный.– М: Айрис Пресс, 2005. – 279 c.

3. Высшая математика в упражнениях и задачах / П.Е. Данко и др. –М: Высшая школа, 1999. – 532 c.

4. Сборник задач по математике для втузов, ч. 1 / А. В. Ефимов, Б. П. Демидович – М: Наука, 1993. – 623 с.

 

Содержание

 

1. Задания по теме «Математический анализ»………………………...3

2. Варианты типовых заданий…………………………………….. 4 –18

3. Справочный материал………………………………… ……......19–23

4. Пример решения типового задания…………………………….24–31

5. Список рекомендуемой литературы………………………………..31