Министерство образования и науки Украины
Севастопольский Национальный Технический Университет
Выполнение статистических расчётов с помощью ЭВМ в системе «Gretl» и «MS Office Excel»
Методические указания к выполнению лабораторной работы № 1
по дисциплине «Прикладная статистика»
Севастополь
Г.
УДК 658.
Выполнение статистических расчётов с помощью ЭВМ в системе «Gretl» и «Ms Office Excel». Методические указания по выполнению лабораторной работы по дисциплине «Прикладная статистика» / Сост. Букач Б.А., Погорелова М.В., Черноморченко К.А. - Севастополь: Изд-во СевГТУ, 2008. - 20 с.
Целью методического указания является ознакомление с возможностями статистического пакета «Gretl» и выполнение простейшего статистического анализа. Методические указания предназначены для студентов экономических специальностей всех форм обучения.
Методические указания содержат описание способов анализа данных в статистическом пакете «Gretl».
Методические указания рассмотрены и утверждены на заседании кафедры МЭМ, (протокол № ____ от “___”____________2008 г.)
Допущено учебно-методическим центром СевГТУ в качестве методических указаний
Рецензент:
- нормоконтроль
СОДЕРЖАНИЕ
Министерство образования и науки Украины.. 1
Севастопольский Национальный Технический Университет. 1
1. Основные характеристики распределения экономических величин. 4
2. Расчёт статистических характеристик величин с помощью «Gretl». 10
5. Варианты заданий по выполнению лабораторной работы.. 19
Контрольные вопросы…………………………………………………………..27
7. Библиография……………………………………………………………………28
Цель работы: получение практических навыков работы со статистическим пакетом «Gretl» и проведения расчётов в программе «MS Office Excel» при расчёте и анализе основных статистических показателей.
В ходе выполнения лабораторной работы студент должен получить практические навыки и умения по следующим пунктам:
- открывать и исследовать уже существующие файлы. Вводить новую информацию, создавать файлы;
- вносить новые изменения в эти файлы, с помощью арифметических функций, для уже существующих данных;
- описывать характер используемых переменных, используя основы статистики;
- сортировать и ранжировать данные;
- создавать графики на основе данных рабочего файла;
- рассчитать коэффициент корреляции двух величин из рабочего файла;
- завершение работы в статистическом пакете «Gretl».
Основные характеристики распределения экономических величин
Исходным материалом любого статистического исследования являются совокупность результатов наблюдений. В простейших случаях они представляют собой выборочные (полученные в результате наблюдений) значения некоторой случайной величины X. В задачах статистики распределение этой случайной величины зачастую неизвестно.
Пусть есть N наблюдений некоторой величины X ( ).Основными статистическими параметрами данной величины являются следующие:
).Основными статистическими параметрами данной величины являются следующие:
1. Среднее значение  вычисляется по формуле:
вычисляется по формуле:
 (1)
(1)
Среднее показывает «центральное положение» (центр) переменной и рассматривается совместно с доверительным интервалом. Обычно интерес представляют статистики (например, среднее), дающие информацию о генеральной совокупности в целом. Чем больше размер выборки, тем более надежна оценка среднего. Чем больше изменчивость данных (больше разброс), тем оценка менее надежна.
2. Дисперсия – наиболее употребительная мера рассеивания, т. е. отклонения от среднего. Вычисляется по следующей формуле:
 (2)
(2)
3. Среднеквадратическое (стандартное) отклонение равна квадратному корню из дисперсии и вычисляется по формуле:
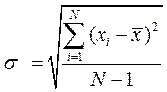 (3)
(3)
Стандартное отклонение ‑ это широко используемая мера разброса или вариабельности (изменчивости) данных.
Среднеквадратическое отклонение показывает средний разброс данных относительно своего среднего значения.
4. Медиана ‑ это значение, которое разбивает выборку на две равные части. Половина наблюдений лежит ниже медианы, и половина наблюдений лежит выше медианы.
Медиана вычисляется следующим образом. Изучаемая выборка упорядочивается в порядке возрастания. Получаемая последовательность ak (k=1,..., 2*m+1)называется вариационным рядом, или порядковыми статистиками. Если число наблюдений нечетно, то медиана оценивается как: am+1. Если число наблюдений четно, то медиана оценивается как:
 (4)
(4)
5. Мода ‑ величины признака (варианта), которая чаще всего встречается в данной совокупности.
6. Коэффициент вариации ‑ используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Вычисляется по формуле:
 (5)
(5)
где σ – среднеквадратическое (стандартное) отклонение;
 ‑ среднее значение.
‑ среднее значение.
Чем меньше коэффициент вариации, тем меньше колеблемость признака, и наоборот.
7. Коэффициент ассиметрии выборки ‑ мера смещённости распределения относительно среднего арифметического значения. Вычисляется по формуле:
 (6)
(6)
где  ‑ среднее арифметическое значение выборки Х;
‑ среднее арифметическое значение выборки Х;
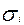 ‑ точечная оценка среднеквадратического отклонения выборки Х;
‑ точечная оценка среднеквадратического отклонения выборки Х;
E(t) ‑ наиболее вероятная оценка параметра t.
Отрицательный коэффициент асимметрии соответствует распределению, смещенному влево относительно среднего значения.
Положительный коэффициент асимметрии соответствует распределению, смещенному вправо относительно среднего значения.
Для нормального закона, или любого другого симметричного распределения, коэффициент асимметрии равен нулю.
8. Коэффициента эксцесса [1] – мера «пикообразности» распределения случайной величины (термин был впервые введен Пирсоном в 1905 г.). Данный показатель вычисляется по формуле:
 (7)
(7)
где 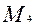 ‑ центральный момент четвертого порядка;
‑ центральный момент четвертого порядка;
 ‑ стандартное отклонение, возведённое в четвёртую степень.
‑ стандартное отклонение, возведённое в четвёртую степень.
Эксцесс может быть охарактеризован дисперсией и среднеквадратическим отклонением, которые вычисляются по следующим формулам:
 (8)
(8)
где N – число наблюдений в выборке.
 (9)
(9)
Если эксцесс положителен, то кривая распределения имеет более высокую и более «острую» вершину, чем нормальная кривая. Если эксцесс отрицателен, то кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая.
9. Доверительный интервал для среднего задает область вокруг среднего, в которой с заданным уровнем доверия (точностью) содержится «истинное» среднее генеральной совокупности.
Например, если среднее в Вашей выборке равно 23, а нижняя и верхняя границы для p =.05 равны 19 и 27 соответственно, то Вы можете заключить, что с 95% вероятностью среднее выборки больше 19 и меньше 27. Если Вы установите меньшее значение p-уровня, то интервал будет шире, и увеличится «уверенность» в оценке, и наоборот. Как мы знаем из прогнозов погоды, чем «неопределеннее» прогноз (т.е. шире доверительный интервал), тем скорее он сбудется.
Заметим, что ширина доверительного интервала зависит от размера выборки и дисперсии наблюдений. Вычисление доверительных интервалов основывается на предположении, что переменная в совокупности нормально распределена. Эта оценка может быть неверной, если это предположение не выполнено, и пока размер выборки мал, например, N меньше 100.
10. Коэффициент корреляции Пирсона (обозначается как r) также называется линейной корреляцией, т.к. измеряет степень линейных связей между переменными.
Можно сказать, что корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения.
Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах.
Пропорциональность означает просто линейную зависимость.
Корреляция высокая, если на графике зависимость можно представить прямой линией с положительным или отрицательным углом наклона (см. Рисунок 1-3). Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленная по оси Y) от наблюдаемых точек до прямой является минимальной из всех возможных. Заметим, что использование квадратов расстояний приводит к тому, что на оценки параметров сильно влияют выбросы.
Корреляция Пирсона предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале.
Коэффициент корреляции Пирсона вычисляется следующим образом:
 (10)
(10)
где 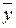 ‑ среднее значение случайной величины Y;
‑ среднее значение случайной величины Y;
 ‑ среднеквадратическое отклонение случайной величины X;
‑ среднеквадратическое отклонение случайной величины X;
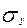 ‑ среднеквадратическое отклонение случайной величины Y.
‑ среднеквадратическое отклонение случайной величины Y.
Коэффициент корреляции изменяется в диапазоне от -1 до +1. Чем больше по модулю коэффициент, тем сильнее связь между изучаемыми переменными.
Например, между ценой и спросом на товар в случае высокой эластичности спроса будет наблюдаться сильная отрицательная корреляция, что отражено на Рисунке 1.
По оси ОY отложены значения цены товара – Р (от англ. яз. «price» ‑ цена).
По оси ОХ отложены значения спроса, т.е. количество проданного товара, ‑ Q (от англ. яз. «quantity» ‑ количество, объём).
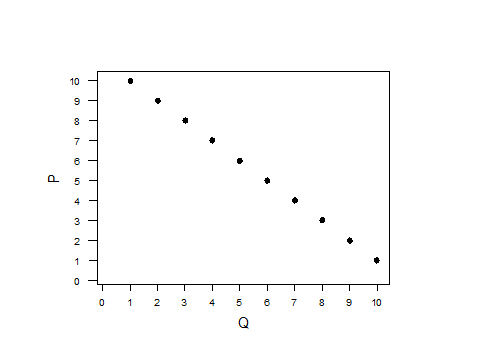
Рисунок 1.1 – График зависимости между ценой товара и спросом на него в случае высокой эластичности спроса
Таким образом, в данном случае коэффициент корреляции будет равен ‑1, т.е. связь отрицательная.
В то же время, между ценой на товар и предложением его на рынке будет наблюдаться сильная корреляция, что отражено на рисунке 2.

Рисунок 1. 2. – График зависимости между ценой на товар и предложением его на рынке
Таким образом, в данном случае коэффициент корреляции будет равен +1, т.е. связь положительная.
В случае, если связи между рассматриваемыми переменными нет, то коэффициент корреляции будет стремиться к нулю (см. рисунок 3).
По оси ОY отложены значения объёма продаж некоторого магазина m5 в тыс. грн. в течение девяти месяцев его работы.
По оси ОХ отложены значения объёма продаж некоторого магазина m6 в тыс. грн. в течение девяти месяцев его работы.
Величина коэффициента корреляции равна 0,22. Т.е. связи между объёмами продаж двух рассматриваемых магазинов нет.

Рисунок 1.3 – График зависимости объёмов продаж двух магазинов в течение девяти месяцев работы, тыс. грн.
11. Таблица частот, или гистограмма, позволяет наглядно оценить частоты попадания случайной величины в определенные интервалы значений.
Общий вид гистограммы представлен на рисунке 4.
В таблице 1 представлен статистический ряд, для которого строилась гистограмма.
Таблица 1.1 – Исходные данные для построения гистограммы

Рисунок 1.4 – Гистограмма
По оси ОY отложены значения частот.
По оси ОХ отложены интервалы.
2. Расчёт статистических характеристик величин с помощью «Gretl»
Для расчёта характеристик статистического ряда величин необходимо:
1. подготовить, ввести, импортировать и сохранить данные.
2. открыть файл с исходными данными.
Получение описательной статистики статистического ряда.
Для получения описательной статистики необходимо выбрать один или более исследуемых рядов данных, а затем пункт меню View – Summary statistics.
Результаты выполнения команды Summary statistics для двух рядов (прибыль – profit и объем продаж - sales) показаны на рисунке 1.1.

Рисунок 2.1 – Результаты Внешний вид окна Summary Statistics.
На рисунке 2.1. отображены следующие результаты:
MEAN – среднее значение;
MEDIAN – значение медианы;
MIN и MAX – минимальное и максимальное значение заработной платы.
S.D. – среднеквадратическое отклонение;
C.V. - коэффициент вариации
SKEW – коэффициент ассиметрии выборки
EXCKURT – коэффициент эксцесса.
2.2. Расчёт коэффициента корреляции. Для этого необходимо выполнить следующие действия: view > Correlation matrix. На экране появится следующее диалоговое окно:
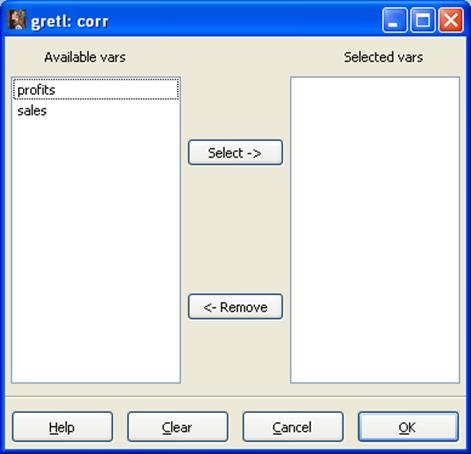
Рисунок 2.2 - Внешний вид окна Correlation matrix.
Для получения коэффициента корреляции между величиной прибыли и объемом продаж необходимо указать в окне «Переменные» (Selected vars) переменные profit, sales. В результате выполнение данной операции в окне результатов появятся следующие данные:

Рисунок 2.3. – Результат расчета коэффициента корреляции
Если в окно переменных (см. рисунок 2.2.) выбрать несколько переменных, то в результом расчетов будет корреляционная матрица (см. рисунок 2.4).

Рисунок 2.4. – Корреляционная матрица
2.3. Построение графиков. Построение графиков в среде Gretl возможно следующими способами:
2.3.1. путем выбора команды x-у graph в главном меню (кнопка  ) и заполнения диалогового окна. В этом случае будет получен точечный график с аппроксимацией линейной функции методом наименьших квадратов. (см. рисунок 2.5)
) и заполнения диалогового окна. В этом случае будет получен точечный график с аппроксимацией линейной функции методом наименьших квадратов. (см. рисунок 2.5)

Рисунок 2.5 – Зависимость безработицы от времени.
2.3.2 путем выбора меню View – Graph specified vars
Данная функция позволяет строить следующие виды графиков:
Time series plot – график временного ряда (см. рисунок 2.6)

Рисунок 2.6 – График временных рядов уровня цен и безработицы.
x-y – scatter – график зависимости одной переменной от другой (аналогично рисунку 2.5)
x-y – with impulses -график зависимости одной переменной от другой в форме столбчатой диаграммы (т.н. импульсов)
И др.
2.3.3. Пункт меню View – Multiply graphs – позволяет строить сразу несколько графиков.

Рисунок 2.7 – Графики уровня цен, безработицы и инфляции в зависимости от периода времени.
При построении графиков в любом режиме и меню необходимо выполнить стандартный набор действий:
- указать какая из колонок будет являться X, а какая Y.
- нажать OK или клавишу «Enter».
Появившийся на экране появится график можно скопировать в буфер с помощью контекстного меню (правая кнопка мыши – Copy to clipboard).
2.4. Для того, чтобы получить гистограмму распределения частот, необходимо выбрать пункт меню: Variable – frequence plot и заполнить диалоговое окно, показанное на рисунке 2.8

Рисунок 2.8 – Внешний вид диалогового окна frequency distribution.
Number of bins – здесь необходимо задать число диапазонов частот.
Если выбрать опцию Minimum value, left bin – то необходимо задать минимальное значение левого промежутка диапазона частот и bin width – ширину частотного диапазона.
Show data only – показывает только данные
Show normal distribution – показывает нормальное распределение.
Show gamma distribution – показывает гамма-распределение.
Гистограмма в gretl показана на рисунке 2.9.
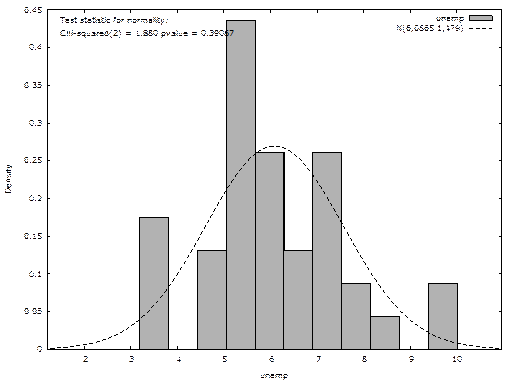
Рисунок 2.9 – Гистограмма безработицы с нормальным распределением.
Если в ходе выполнения лабораторной работы вы использовали файл с базы данных, встроенной в «Gretl», то необходимо оба раза выбрать ответ "Нет", так как в противном случае вы можете испортить базу данных. Если же в ходе лабораторной работы вы использовали ваш файл, то вы можете записать его на винчестер.






