Зміст
вступ.. 4
1. Кореляційно-регресійний аналіз. 4
2. Приклад.. 9
3. оформлення роботи.. 13
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ.. 14
ДОДАТОК.. 15
Вступ
Методичні вказівки призначенідля практичного освоєння теоретичного курсу статистики з теми “Кореляційно-регресійний аналіз” на конкретному прикладі в процесі виконання курсової роботи. Письмове виконання курсової роботи сприяє не тільки поглибленому вивчанню методів статистики, але й придбанню практичних навичок з розрахунку статистичних показників, правильної побудови й оформлення таблиць, графіків. Основна мета розробок – навчити розумінню суті розрахункових показників та їхнього аналізу.
Керівник курсової роботи видає студентові завдання з вихідними даними, у т.ч. - на тему “ Кореляційно-регресійний аналіз ”, і встановлює порядок, обсяг і термін завершення розрахунків, аналізу і підготовки до захисту.
Керівник роботи:
- контролює процес виконання роботи;
- рекомендує літературу і довідкові матеріали;
- проводить консультації зі студентами;
- допомагає в обробці вихідних даних і в складанні висновків;
- перевіряє виконані розрахунки.
Перед рішенням кожної задачі необхідно ретельно вивчити її зміст.
Перш ніж приступати до практичного виконання завдань, варто уважно ознайомитися із відповідним матеріалом методичних вказівок та літературою з рекомендованого списку.
Кореляційно-регресійний аналіз
Сучасна наука виходить із взаємозв'язку всіх явищ природи та суспільства.
Розрізняють 2 типи зв'язків між різними явищами і їхніми ознаками: функціональний (жорстко детермінований) і статистичний (стахостично-детермінований) зв'язок.
Якщо зі зміною значення однієї з перемінних друга змінюється строго певним чином, тобто значенню однієї перемінної відповідає одне точно задане значення іншої перемінної, - то зв'язок між ними є функціональним.
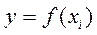(наприклад, 
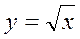) - функціональний зв'язок.
Стохастично детермінований зв'язок не має обмежень і умов, властивих функціональним зв'язкам.
Якщо зі зміною значення однієї з перемінних друга приймає у визначених межах будь-яке значення, то зв'язок називається стохастичним, тобто при різних значеннях однієї перемінної існують відповідні різні значення іншої перемінної.
Модель стохастичного зв'язку:
,
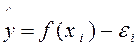де f (xi) - частина результативної ознаки, що сформувалася під впливом врахованих, відомих факторних ознак (одного чи безлічі).
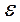i - частина результативної ознаки, що виникла як слідство дії неконтрольованих, неврахованих факторів.
Кореляційним зв'язком називають найважливіший окремий випадок стохастической зв'язку, що складається в тому, що різним значенням однієї перемінної відповідають різні середні значення іншої.
Кореляційний зв'язок між ознаками може виникати різними шляхами:
1) Причинна залежність результативної ознаки від варіації факторної ознаки.
2) Зовсім інша інтерпретація необхідна для вивчення кореляційного зв'язку між двома наслідками загальної причини.
3) Виникнення кореляції: взаємозв'язок ознак, кожна з яких є і причина і наслідок.
Оскільки кореляційний зв'язок є статистичним, першою умовою можливості її вивчення є наявність даних по досить великій сукупності явищ.
Головною характеристикою кореляційного зв'язку є вивчення лінії регресії.
Теоретичною лінією регресії називається та лінія, навколо якої групуються крапки кореляційного поля, і яка вказує основний напрямок, тенденцію. Ця лінія повинна бути проведена так, щоб сума відхилень крапок поля кореляції від відповідних крапок теоретичної лінії регресії, дорівнювала нулю, а сума квадратів цих відхилень була б мінімальною.
Кореляційно-регресійний аналіз (КРА) складається з наступних етапів:
1) вибір форми регресії;
2) визначення параметрів рівня;
3) оцінка тісноти зв'язку;
4) перевірка адекватності моделі рівняння.
Найбільш часто використовуються для характеристики економічних показників наступні типи функцій:
|
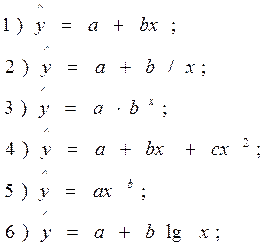
Найбільш часто застосовується в статистичному аналізі - лінійна функція:
Y = a + bx,
де а - вільний член рівняння;
b - коефіцієнт регресії, що показує на скільки одиниць у середньому змінюється величина результативної ознаки U при зміні факторної ознаки х на одиницю.
Визначення параметрів рівняння регресії виконується методом найменших квадратів, основною умовою якого є мінімізація суми квадратів відхилень емпіричних значень від теоретичних.
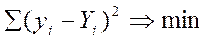
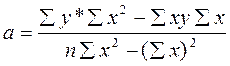
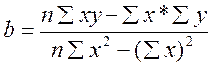
Дисперсію теоретичних значень називають факторною й обчислюють за формулою:
Факторна дисперсія:
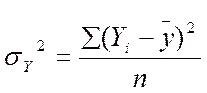
Замість середньої з внутрішньогрупової дисперсії обчислюють залишкову (випадкову) дисперсію.
Залишкова дисперсія:
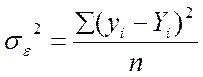
Загальна дисперсія:
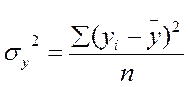
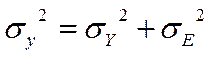
Мірою тісноти зв'язку є коефіцієнт детермінації:
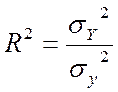
Тісноту зв'язку характеризує індекс кореляції:
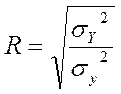
Кореляційно-регресійний аналіз може проводитися в умовах малої вибірки, тобто для обмеженого обсягу сукупності.
Щоб перевірити, наскільки ці показники характерні для всієї генеральної сукупності і чи не є вони результатом збігу випадкових обставин, необхідно перевірити адекватність статистичних спостережень. При чисельності об'єктів аналізу до 30, виникає необхідність перевірки значимості кожного коефіцієнту регресії.
Значимість коефіцієнту простої лінійної регресії визначається за допомогою критерію Фішера ( F).
,
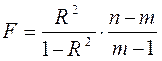де m – число параметрів в рівнянні регресії (=2);
n – обсяг сукупності (кількість досліджень =10).
Параметр визнається значимим за умови, якщо tрозр. > tтабл. (табличне значення див. у додатку).
Приклад
За допомогою методу КРА визначимо наявність і характер статистичного зв'язку між ознаками «вік устаткування» і «витрати на ремонт».
Таблиця 2.1
Дослідження статистичного зв`язку між ознаками
«вік устаткування» і «витрати на ремонт» для групи підприємств
| № з/п | Вік обладнання хі | Витрати на ремонт уі | 
| 
|
| 
| 
| 
|
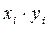
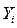
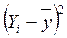
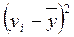
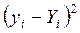
| 1,5 | 0,87 | 3,36 | 1,44 | 0,40 | ||||
| 1,48 | 1,49 | 0,49 | 0,27 | |||||
| 1,4 | 1,48 | 1,49 | 1,69 | 0,01 | ||||
| 2,3 | 13,8 | 2,09 | 0,37 | 0,16 | 0,04 | |||
| 2,7 | 21,6 | 3,31 | 0,37 | 0,37 | ||||
| 4,53 | 3,36 | 1,69 | 0,28 | |||||
| 2,3 | 18,4 | 3,31 | 0,37 | 0,16 | 1,02 | |||
| 2,5 | 17,5 | 2,70 | 0,00 | 0,04 | 0,04 | |||
| 6,6 | 72,6 | 5,15 | 5,98 | 15,21 | 2,10 | |||
| 1,7 | 10,2 | 2,09 | 0,37 | 0,15 | ||||
| Разом: | 70 | 27 | 536 | 217,1 | 27 | 17,17 | 21,88 | 4,69 |
1) Виходячи з цих даних виберемо форму регресії у вигляді однофакторної моделі залежності витрат на ремонт від віку устаткування.
Порівнявши середні значення результативної ознаки по групам, можна зробити висновок, що збільшення віку обладнання спричиняє збільшення витрат на ремонт обладнання, тобто можна припустити наявність прямої кореляційної залежності між ознаками.
Отже, між х і у існує пряма залежність. В основі цієї залежності лежить прямолінійний зв'язок, що може бути виражено простим лінійним рівнянням регресії: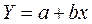 
. Користуючись розрахунковими значеннями (див. табл. 2.1), визначимо параметри для даного рівняння регресії:
2) обчислимо параметри рівняння:
Параметри рівняння:
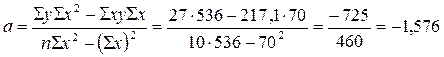
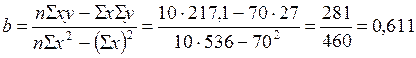
Розрахунок параметру а можна перевірити за допомогою рівняння:
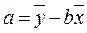
де:
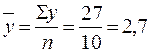(ум. гр. од.);
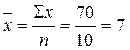(років)
Звідси:
.
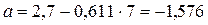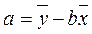=-1,576.
Рівняння регресії має вид: Y = -1,576 + 0,611*х.
Результати проміжних розрахунків приведені в таблиці 2.1.
3) оцінимо тісноту зв'язку:
Коефіцієнт детермінації. У моделі аналітичного угрупування мірою щільності зв'язку є відношення факторної дисперсії до загальної, яке називають емпіричним коефіцієнтом детерміації:
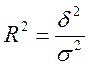
де δ2 – факторна дисперсія:
= 
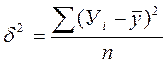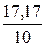= 1,717
s2 - загальна дисперсія:
= 
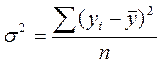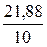= 2,188
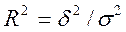= 1,717 / 2,188 = 0,785.
Кореляційне відношення показує тісноту зв'язку між групувальною та результативною ознаками. Може приймати значення від 0 до 1. Чим вище значення, тим більш функціональною є залежність між показниками, тісніше зв'язок.
Коефіцієнт кореляції:
.
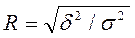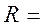0,886.
Згідно якісній оцінці тісноти зв'язку Чеддока (див. Методичні вказівки щодо виконання курсової роботи з курсу «Статистика» за темою «Статистичні ряди розподілу»), у нашому прикладі існує тісна сила зв'язку між розмірами витрат на ремонт і віком устаткування.
4) перевіримо значимість коефіцієнта регресії з вірогідністю 0,95.
При чисельності об'єму аналізу до 30 одиниць виникає необхідність перевірки значимості.
Перевірку значимості рівняння регресії можна виконати на основі обчислення F-критерію Фішера:
,
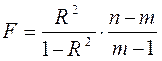де m – число параметрів в рівнянні регресії (=2);
n – кількість досліджень (=10).
Визначаємо Fтабл. по таблиці (див. додаток) для вірогідності 0,95. Ступені вільності залежать від числа параметрів рівняння регресії: k1=m-1 і кількості одиниць досліджуваної сукупності: k2 = n-m.
Для k1=1, k2=8 Fтабл = 5,32.
Fрозр = 0,785/(1-0,785)* (10-2)/(2-1) = 29,2.
Оскільки Fрозр =29,2 набагато більше критичного Fтабл =5,32, що підтверджує істотність кореляційного зв’язку, то рівняння регресії
Y = -1,576 + 0,611 слід визнати адекватним у 95 випадках з 100.
5) визначимо коефіцієнт еластичності.
Коефіцієнт еластичності показує середні зміни результативної ознаки при зміні факторної ознаки на 1%:
.
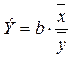Э = 0,611 х 7 / 2,7 = 1,58.
Висновок:
Було зроблено припущення щодо наявності лінійного зв’язку між віком устаткування та витратами на ремонт. В результаті такого припущення було складено рівняння регресії: Y = -1,576 + 0,611*х, яке свідчить, що із збільшенням віку устаткування витрати на ремонт також збільшуються. Збільшення віку устаткування, згідно з початковими даними, на 1 рік, - призводить до збільшення витрат на ремонт на 0,611 ум.гр.од.
Коефіцієнт детермінації дорівнює 0,785. Звідси можна допустити, що 78,5% загальної варіації витрат на ремонт обумовлено варіацією чинника – віку устаткування, а 21,5% (100-78,5) - загальною варіацією з причин дії інших факторів.
Перевірка за допомогою F -критерію Фішера з рівнем значимості 0,95 довела, що рівняння регресії Y = -1,576 + 0,611 слід визнати адекватним у 95 випадках із 100, а висновки з достатньою вірогідністю можна поширювати на всю гіпотетичну генеральну сукупність.
Коефіцієнт еластичності показав, що зі зміною віку обладнання на 1% - витрати на ремонт зростають в середньому на 1,58%.
Оформлення роботи
Розрахунково-графічна робота має бути написана на односторонніх аркушах білого папера формату А4 (210х297мм). Текст розрахунково-графічної роботи виконують:
- машинописним способом – шрифтом Times New Roman або Times New Roman Cyr із розміром шрифта 14 пт через 1,5 інтервали;
- рукописним.
Відстань (поля) від краю листа до тексту не менш, мм: ліве – 25, праве, верхнє й нижнє – 15.
Абзаци в тексті починаються відступом, рівним 1,25 мм.
Вписувати в текстові документи, виготовлені машинописним способом, окремі слова, формули, умовні знаки (рукописним способом) слід чорними чорнилами або пастою, при виконанні ілюстрацій рекомендується використовувати різні кольори.
Вписування тексту між рядків не допускається.
Помилки, описки і графічні неточності, виявлені в процесі виконання документа, допускається виправляти акуратним підчищенням або зафарбовуванням «штрихом» і нанесенням на тому ж місці виправленого тексту (графіки) машинописним способом або рукописним способом - чорними чорнилом, пастою чи тушшю.
Нумерація листів повинна бути наскрізною у правому нижньому куті. Першою сторінкою є титульний лист. На титульному листі роботи номер не ставлять.
Формули та таблиці нумеруються наскрізною нумерацією арабськими цифрами в межах розділу. Номера формул записують на рівні формули праворуч у круглих дужках: (1.1), (1.2), і т.інш.
