4 семестр
1. Опр. мнимой единицы, комплексного числа (КЧ), свойства сопряженных КЧ.
2. Правила сложения, умножения, деления КЧ в алгебраической форме.
3. Геометрическая интерпретация КЧ, опр. модуля и аргумента, их обозначения.
4. Тригонометрическая форма КЧ. Правила умножения, деления КЧ.
5. Каким образом при извлечении корня n –ой степени из КЧ появляются n его значений?
6. Опр.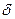 
- окрестности точки, области, границы области на плоскости. Типы областей.
7. Опр. функции комплексной переменной (ФКП), её геометрический смысл.
8. Как определяются функции ez, sin z, cos z, sh z, ch z? Формула Эйлера, её доказательство. Связь между гиперболическими и тригонометрическими функциями.
9. Опр. производной ФКП. Какая функция наз. дифференцируемой в точке и аналитической в области?
10. Какое требование к производной от ФКП приводит к появлению условий Коши – Римана?
11. Как записываются условия Коши – Римана?
12. Чем различаются общие правила дифференцирования аналитических функций и функций действительной переменной?
13. Опр. гармонических функций. Как записывается уравнение Лапласа?
14. Геометрический смысл модуля и аргумента производной ФКП. Главная особенность конформного отображения.
15. Как формируется интегральная сумма криволинейного интеграла ФКП вдоль кривой? Какую окончательную форму принимает криволинейный интеграл от ФКП?
16. Перечислить общие свойства криволинейных интегралов.
17. Формула для вычисления криволинейного интеграла вдоль кривой y = y(x) от а до b.
18. Теорема Коши для односвязной области. Идея доказательства.
19. Теорема Коши для кольцевой области. Идея доказательства.
20. Опр. неопределенного интеграла ФКП.
21. Основная теорема интегрального исчисления.
22. Интегральная формула Коши. Что и как она определяет?
23. Как записывается интегральное представление n – ой производной ФКП?
24. Каким образом от интегральной формулы Коши переходят к разложению ФКП в степенной ряд? Дать опр. ряда Лорана и области его сходимости.
25. При каком условии ФКП разлагается только в ряд Тейлора. Формула разложения.
26. Перечислить три типа изолированных особых точек. Их связь с рядом Лорана.
27. Дать опр. порядка нуля ФКП и правила опр. порядка полюса.
28. Как определяется порядок нуля ФКП путем дифференцирования?
29. Опр. вычета ФКП. Теорема о вычетах. Идея доказательства.
30. Какие условия накладывают на ФКП теорема Коши для односвязной области и теорема о вычетах?
31. Формулы для вычисления вычетов полюса первого порядка.
32. Формула для вычисления вычетов полюса n -ого порядка.
33. Как вычислить по формуле Коши интеграл по замкнутому контуру от ФКП, имеющей многочлен в знаменателе?
34. Почему интеграл от действительной переменной по бесконечным пределам в некоторых случаях сводится к вычислению вычетов?
35. Какие требования предъявляются к функции – оригиналу?
36. Дать определение преобразования Лапласа. В чем выгода от его применения?
37. Почему преобразование Лапласа обладает свойством линейности?
38. Прочитать теорему подобия.
39. Прочитать теорему запаздывания.
40. Прочитать теорему смещения.
41. Теорема о дифференцировании оригинала.
42. Теорема о дифференцировании изображения.
43. Теорема об интегрировании оригинала.
44. Теорема об интегрировании изображения.
45. Определение свертки функций и её главное свойство.
46. Опр. комбинаторики. Основные типы выборок, их название, отличие, число.
47. Назвать базовые понятия теории вероятностей.
48. Опр. случайного события, достоверного, невозможного. Опр. несовместных, противоположных, равновозможных событий. Что такое полная группа событий?
49. Общее опр. вероятности. Три модели вычисления вероятностей, их главные особенности.
50. Что такое сумма и произведение случайных событий?
51. Теоремы сложения вероятностей для несовместных и совместных случайных событий.
52. Теорема умножения вероятностей для независимых событий.
53. Опр. зависимых событий, условной вероятности. Вероятность произведения двух зависимых событий.
54. Какую ситуацию описывает формула Бернулли и как она записывается?
55. Какую ситуацию описывает формула полной вероятности и как она записывается?
56. Опр. случайной величины (СВ). Два типа СВ.
57. Как записывается в общем вид закон распределения и функцию распределения вероятностей дискретных СВ
58. Опр. функции распределения вероятностей непрерывной СВ, ее общие свойства.
59. Опр. плотности распределения вероятностей, её общие свойства.
60. Как записывается общая формула вероятности появления СВ на промежутке (а,b).
61. Опр. математического ожидания дискретной СВ. Перечислить общие свойства.
62. Опр. дисперсии дискретной СВ. Перечислить общие свойства.
63. Как записываются формулы для математического ожидания, дисперсии и среднего квадратичного отклонения для непрерывных СВ.
64. С какой вероятностью появляется СВ n в биноминальном распределении? Чему равны математическое ожидание, дисперсия, среднее квадратичное отклонение?
65. С какой вероятностью появляется СВ n в распределении Пуассона? Чему равны математическое ожидание, дисперсию, среднее квадратичное отклонении?
66. Как записывается дифференциальный закон формирования показательного распределения?
67. Какой вид имеет плотность вероятности, функция распределения, математическое ожидание, дисперсия, среднее квадратичное отклонение для показательного распределения СВ?
68. Какой вид имеет функция надежности? Объяснить её смысл.
69. Как записывается дифференциальный закон формирования нормального распределения.
70. Записать нормальный закон распределения, объяснить смысл параметров.
71. Смысл центральной предельной теоремы теории вероятностей.
72. Как записывается исходная формула вероятности нормального распределения N(x;m, s) для СВ на промежутке (a,b).
73. Как записывается плотность нормированного и центрированного нормального распределения и интеграл вероятностей.
74. Записать формулу вероятности нормального распределения N(x;m, s) для СВ на промежутке (a,b) через функцию Лапласа.
75. В чем основная задача математической статистики?
76. Чем отличается выборка СВ от генеральной совокупности?
77. Чем отличаются частота и относительная частота выборки СВ?
78. Что такое статистический ряд и статистический ряд по интервалам.
79. Как рисуется полигон и гистограмма выборки СВ?
80. Записать эмпирическую функцию распределения выборки СВ.
81. Что такое функция выборки? Что такое точечная оценка параметра?
82. Какие оценки параметра наз. состоятельными?
83. Содержание теоремы Чебышева.
84. Опр. несмещенной и асимптотически несмещенной точечной оценки параметра.
85. Содержание теоремы Бернулли.
86. Опр. статистической дисперсии СВ Х. Почему эта точечная оценка оказывается асимптотически состоятельной?
87. Как выражается дисперсия среднего арифметического значения СВ Х через дисперсию генеральной совокупности
88. Опр. доверительного интервала точечной оценки.
89. Что такое статистическая гипотеза? Привести примеры выдвижения гипотез, исходя из общего вида гистограмм.
