Если задача содержит только две переменные, а система ограничений задана в виде неравенств, то её можно решить графическим методом.
Графический метод решения ЗЛП состоит из следующих этапов.
1. Строится область допустимых решений (ОДР) ЗЛП.
2. Строится вектор-градиент целевой функции (вектор, координатами которого являются частные производные функции) с приложением в начале координат – 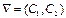 .
.
3. Линия уровня C1x1+C2x2 = а (а – постоянная величина) - прямая, перпендикулярная вектору–градиенту 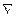 – передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
– передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
4. Для нахождения ее координат достаточно решить систему из двух уравнений прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1,x2), найденное в полученной точке, является максимальным.
При минимизации f(x1,x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то целевая функция f(x1,x2) не ограничена на максимум (в задаче максимизации) или минимум (в задаче минимизации).
Если линия уровня параллельна какой-либо прямой из ограничений задачи, то оптимальное значение целевой функции будет достигаться в любой точке этой прямой.
Пример. Найти максимальное значение функции f=2x1 + 3x2 при условиях
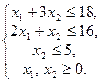
Построим область допустимых значений:
1) первое ограничение x1 + 3x2 £ 18; прямая x1 + 3x2 = 18 пересекает оси координат в точках (0; 6) (18; 0); неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка(0; 0), 0 + 3*0 < 18 принадлежит полуплоскости);
2) второе ограничение 2 x1 + x2 £ 16: прямая 2x1 + x2 = 16 пересекает оси координат в точках (0; 16) (8; 0); неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка (0; 0), 2*0 + 0 <16 принадлежит полуплоскости);
3) неравенству x2 £ 5 соответствует полуплоскость, содержащая прямую x2 = 5 и лежащая ниже неё.
4) x1 ³ 0 - правее ОX2;
5) x2 ³ 0 - выше ОX1.
Вектор-градиент имеет координаты 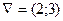 .
.
Построим линии уровня 2 x1 + 3 x2 = а. При а = 0 получим прямую 2x1 + 3x2 = 0, проходящую через начало координат, перпендикулярно вектору-градиенту. Так как задача на максимум, то передвигаем линию уровня в направлении градиента. Предельной точкой (последней из области допустимых решений, с которой соприкасается линия уровня) является точка С. Значит, в ней достигается максимум функции f (рис. 1).
Найдём её координаты. Для этого решим систему, составленную из уравнений прямых пересекающихся в точке С (I и II):
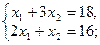
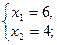
Таким образом, получим x1 = 6, x2 = 4, fmax = 2*6 + 3*4 = 24.
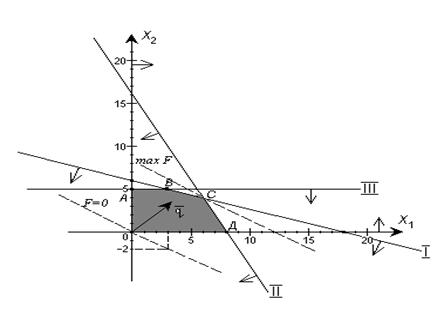 |
Рис. 1.




