Методические указания для выполнения практической части контрольной работы

 

3.3.1 Базовые понятия курса

 

Проценты – это доход от предоставления капитала в долг в различных формах (ссуды, кредиты и т.д.), либо от инвестиций производственного или финансового характера.

Процентная ставка – величина, характеризующая интенсивность начисления процентов.

Величина получаемого дохода (т.е. процентов) определяется исходя из величины вкладываемого капитала, срока, на который он предоставляется в долг или инвестируется, размера и вида процентной ставки (ставки доходности).

Наращение (рост) первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов (дохода).

Множитель (коэффициент) наращения – это величина, показывающая, во сколько раз вырос первоначальный капитал.

Период начисления – промежуток времени, за который начисляются проценты (получается доход). В дальнейшем будет полагаться, что период начисления совпадает со сроком, на который предоставляются деньги. Период начисления может разбиваться на интервалы начисления.

Интервал начисления – минимальный период, по прошествии которого происходит начисление процентов.

Существует две концепции и, соответственно, два способа определения и начисления процентов:

1. Декурсивный способ. Проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из предоставляемого капитала. Соответственно декурсивная процентная ставка (или ссудный процент) представляет собой выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.

2. Антисипативный способ (предварительный). Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала. Определяемая таким образом, процентная ставка называется (в широком смысле слова) учетной ставкой или антисипативным процентом.

В мировой практике декурсивный способ получил наибольшее распространение. В условиях развитой рыночной экономики антисипативный способ применяется, как правило, в период высокой инфляции.

При обоих способах начисления процентов процентные ставки могут быть либо простыми, (если они применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления), либо сложными (если по прошествии каждого интервала начисления они применяются к сумме долга и начисленных за предыдущие интервалы процентов).

В российской практике понятия ссудного процента и учетной ставки обычно не различаются и обозначаются собирательным термином «процентная ставка» (термин «учетная ставка» можно также встретить применительно к ставке рефинансирования Центрального банка и к вексельным операциям).

В связи с этим необходимо подчеркнуть, что по мере развития рыночных отношений вопрос различия декурсивного и антисипативного методов начисления приобретает все большую актуальность.

Финансисту – инвестору (вкладчику), заемщику средств – в любом случае необходимо иметь представление о способе начисления процентов, подразумеваемом в каждой конкретной сделке, тем более, что при укрупнении масштабов операции каждый процентный пункт становится все «тяжелее». Непонимание различия между видами процентных ставок может при этом вылиться не только в упущенную выгоду, но и в значительные убытки.

 

3.3.2 Простые ставки ссудных процентов

 

Простые ставки ссудных (декурсивных процентов) применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Естественно, простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в операции сторон.

Введем следующие обозначения:

- i (%) – простая годовая ставка ссудного процента;

- i – относительная величина ставки процентов;

- Ir – сумма процентных денег, выплачиваемых за год;

- I – общая сумма процентных денег за весь период начисления;

- P – величина первоначальной денежной суммы;

- S – наращенная сумма;

- k_н – коэффициент наращения;

- n – продолжительность периода начисления в годах;

- d – продолжительность периода начисления в днях;

- K – продолжительность года в днях; является временной базой для расчета процентов.

В зависимости от способа определения продолжительности финансовой операции рассчитывается либо точный, либо обыкновенный (коммерческий процент).

Дата выдачи и дата погашения ссуды всегда считаются за один день. При этом возможны два варианта:

- используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года; из номера, соответствующего дню окончания займа, вычитают номер первого дня;

- применяется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням; этот метод используется, когда не требуется большая точность, например при частичном погашении займа.

Точный процент получают, когда за временную базу берут фактическое число дней в году и точное число дней ссуды.

Приведенным выше определениям соответствуют формулы (3.1 – 3.6):

 

I (%)= 100% (3.1)

I = (3.2)

I = I _r n (3.3)

S=P+I (3.4)

k_н = (3.5)

(3.6)

 

Применяя последовательно формулы (3.4), (3.3), (3.2) и (3.6), получаем основную формулу (3.7) или формулу (3.8) для определения наращенной суммы[3]:

 

S = P (1 + ni), (3.7)

или

S = P (1 + i). (3.8)

 

На практике часто возникает обратная задача: узнать величину суммы Р, которая в будущем должна составить заданную величину S. В этом случае Р называется современной (текущей, настоящей^[4], приведенной) величиной суммы S.

Определение современной величины Р наращенной суммы S называется дисконтированием, а определение величины суммы S - компаудингом.

В применении к ставке ссудного процента может также встретиться название математическое дисконтирование, несовместимое с учетными ставками, которые будут рассматриваться в следующем разделе.

Из формулы (3.7) получаем формулу (3.9), соответствующую операции дисконтирования:

P = 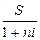(3.9)

 

Преобразуя формулу (3.7) (т.е. заменяя входящие в нее выражения на эквивалентные и выражения на эквивалентные и выражая одни величины через другие), получаем еще несколько формул (3.10 – 3.13) для определения неизвестных величин в различных случаях:

 

P = (3.10)

 

d = K (3.11)

 

i = (3.12)

 

i = K (3.13)

 

Иногда на разных интервалах начисления применяются разные процентные ставки. Если на последовательных интервалах начисления n₁, n₂, n_N используются ставки процентов i₁, i₂, i_N то по формулам (3.2) и (3.3) сумму процентных денег в конце первого интервала рассчитывают по формуле (3.14), в конце второго интервала по формуле (3.15) и т.д. При N интервалах начисления наращенную сумму рассчитывают по формуле (3.16).

 

I₁ = P n₁ i₁ (3.14)

 

I₂ = P n₂ i₂ (3.15)

S = P (1 + ) (3.16)

 

Для множителя наращения, следовательно, используется формула (3.17):

 

kн = 1 + . (3.17)

 

3.3.3 Простые учетные ставки

 

При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (т. е. из наращенной суммы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке, а также коммерческим или банковским учетом.

Дисконтом называется доход, полученный по учетной ставке, т. е. разница между размером кредита и непосредственно выдаваемой суммой.

Введем обозначения:

- d (%) - простая годовая учетная ставка;

- d - относительная величина учетной ставки;

- Dr - сумма процентных денег, выплачиваемая за год;

- D - общая сумма процентных денег;

- S - сумма, которая должна быть возвращена;

- P - сумма, получаемая заемщиком.

Согласно определениям имеем следующие формулы (3.18 – 3.22):

 

D = (3.18)

 

D_г = d S; (3.19)

 

D = n D_г = n d S; (3.20)

 

P = S –D = S (1 – n d) = S (1 - (3.21)

 

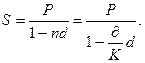(3.22)

 

На практике учетные ставки применяются главным образом при учете (т.е. покупке) векселей и других денежных обязательств.

Период начисления и учетная ставка при прочих заданных условиях определяются по формулам (3.23 – 3.24):

(3.23)

 

(3.24)

3.3.4 Сложные ставки ссудных процентов

 

Если после очередного интервала начисления доход (т. е. начисленные за данный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.

Введем обозначения:

- i _с – относительная величина годовой ставки сложных ссудных процентов;

- k _н.с – коэффициент наращения в случае сложных процентов;

- j – мноминальная ставка сложных ссудных процентов (ее определение будет дано в дальнейшем).

Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой (3.7), составит S ₁= P (1+ i _c). Еще через год это выражение применяется уже к сумме S ₁: S ₂ = S ₁ (1 + i _c) = P (1+ + i _c)².

Очевидно, что по прошествии n лет наращенная сумма будет определяться по формуле (3.25).

 

S = Р (1 + i _c)ⁿ . (3.25)

 

Множитель наращения k _н.с. соответственно будет определяться формулой (3.26).

k _н.с. = (1 + i _c)ⁿ . (3.26)

 

При начислении простых процентов он составил бы (1 + ni) (формулы (3.5) и (3.7).

Очевидно, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов.

Если срок ссуды п в годах не является целым числом, множитель наращения определяют по формуле (3.27).

 

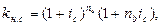(3.27)

где n = n_a+ n_b;

n_a – целое число лет;

n_b – оставшаяся дробная часть года.

 

На практике в данном случае часто предпочитают пользоваться формулой (3.25) с соответствующим нецелым показателем степени. Но нужно иметь в виду, что с точки зрения сущности начисления процентов этот способ является приблизительным, и погрешность при вычислениях будет тем больше, чем больше значения входящих в формулу величин. Следует учитывать, что приблизительный метод дает меньший, чем в действительности, результат.

Таким образом, в современной ситуации, когда номиналы денежных сумм достаточно велики, от этого метода лучше отказаться вовсе.

Если уровень ставки сложных про­центов будет разным на различных интервалах начисления.

Пусть n ₁, n ₂, n_N – продолжительность интервалов начисления в годах; i ₁, i ₂ ,..., i_N - годовые ставки процентов, соответствующие данным интервалам. Тогда наращенная сумма в конце первого интервала начисления в соответствии с формулой (3.7), составит: S ₁ = Р (1 + n ₁ i ₁); в конце второго интервала: S ₂ = Р (1+ n ₁ i ₁) (1+ n₂ i ₂), и т.д.

При N интервалах начисления наращенная сумма в конце всего периода начисления составит:

 

(3.28)

 

Если все интервалы начисления одинаковы (как и бывает обычно на практике) и ставка сложных процентов одна и та же, формула (3.28) трансформируется в формулу (3.29).

(3.29)

 

Начисление сложных процентов может осуществляться не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j - годовая ставка, по которой определяется величина ставки процентов, применяемой на каждом интервале начисления.

При т равных интервалах начисления и номинальной процентной ставке j эта величина считается равной

Если срок ссуды составляет п лет, то, аналогично формуле (3.25), получаем выражение для определения наращенной суммы (формула (3.30):

 

S_mn = P (1 + ) ^mn, (3.30)

где тп – общее число интервалов начисления за весь срок ссуды.

 

Если общее число интервалов начисления не является целым числом (тп – целое число интервалов начисления, l – часть интервала начисления), то формула (3.31):

S = P (1 + ) ^mn (1 + l ). (3.31)

Для целого числа периодов начисления используется формула сложных процентов (формула (3.25), а для оставшейся части – формула простых процентов (формула 3.7).

Проценты, начисляемые с определенной периодичностью (полгода, квартал, месяц, день), называются дискретными. Часто применяется непрерывное начисление сложных процентов (продолжительность интервала начисления стремится к нулю, а т - к бесконечности).

В этом случае для вычисления наращенной суммы служит формула (3.32):

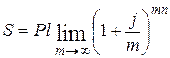. (3.32)

 

Для расчетов можно использовать известную в математике формулу (3.33):

, (3.33)

где е= 2,71828…

 

Из этой формулы следует формула (3.34):

 

(3.34)

 

Тогда для наращенной суммы получаем формулы (3.35-3.36):

 

. (3.35)

 

. (3.36)

 

Значения наращенной суммы S можно вычислять с помощью финансового калькулятора, или находя значения e^jn и других требуемых величин в специальных таблицах (Приложение).

Очевидно, что непрерывный способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях (т. е. при одинаковых п, j, Р).

Аналогично случаю простых процентов полученные формулы можно преобразовывать, выражая одни величины через другие, в зависимости от того, что известно, а что требуется найти.

Так, из формулы (3.25) получаем формулу (3.37):

. (3.37)

 

где Кд – коэффициент дисконтирования – величина обратная коэффициенту

наращения.

Таким образом, из приведенного выше, можно сделать вывод, что текущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности.

Преобразуя формулы (3.25) и (3.30), получаем, соответственно, формулы (3.38) и (3.39):

 

i = - 1 (3.38)

 

j =m (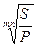 - 1) (3.39)

 

Применяя операцию логарифмирования к обеим частям формулы (3.25), получаем формулу (3.40):

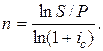(3.40)

 

Подобным же образом из формулы (3.30) получаем формулу (3.41)

 

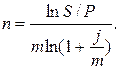(3.41)

 

 

3.3.5 Сложные учетные ставки

 

Антисипативный способ начисления сложных процентов.

Введем обозначения: dс (%) – сложная годовая учетная ставка; dc – относительная величина сложной учетной ставки; k_н.у – коэффициент наращения; f – номинальная годовая учетная ставка.

Тогда по прошествии первого года наращенная сумма S₁ в соответствии с формулой (3.22) составит (формула (3.42), которая еще через год будет применяться уже к сумме S₁(формула 3.43) и т. д., аналогично случаю сложных ставок ссудных процентов. По прошествии п лет наращенная сумма будет определяться формулой (3.44):

 

(3.42)

 

(3.43)

 

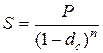. (3.44)

 

Множитель наращения будет определяться по формуле (3.45):

 

(3.45)

 

При сравнении формул (3.25) и (3.44), видно, что при равенстве судного процента и учетной ставки наращение первоначальной суммы во втором случае (антисипативный метод) идет быстрее.

Поэтому в литературе часто можно встретить утверждение, что декурсивный метод начисления более выгоден для заемщика, а антисипативный – для кредитора. Это можно считать справедливым лишь для небольших процентных ставок, когда расхождение не столь значительно. С ростом же процентной ставки разница в величине наращенной суммы значительно увеличивается (при этом она сама растет с ростом п), и сравнение двух методов с точки зрения выгодности утрачивает смысл.

Из формулы (3.44) следует, что для периодов начисления, превышающих один год, учетная ставка может принимать значения только строго меньшие (т. е. не достигающие) 100%. Иначе величины Р или S не будут иметь смысла, становясь бесконечными или даже отрицательными. Наращенная сумма S очень быстро увеличивается с ростом d, стремясь к бесконечности, когда d (%) приближается к 100%.

Так же, как и при декурсивном способе, возможны различные варианты начисления антисипативных процентов (начисление за короткий – меньше года - интервал, начисление т раз в году и т. д.). Так, для периода начисления, не являющегося целым числом соответствует формула (3.46).

 

k _н.у= (3.46)

 

При учетной ставке, изменяющейся в течение срока ссуды, наращенная сумма определяется по формуле (3.47):

 

S = P / 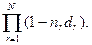(3.47)

 

Для начисления процентов т раз в году формула (3.48) или (3.49):

S = P / (1 - f/m) ^mn (3.48)

 

S = P / [(1 - f/m) ^mn (1 – l f/m)]. (3.49)

 

При непрерывном начислении процентов S рассчитывается по формуле (3.50)

. (3.50)

 

Из полученных формул путем преобразований получаем формулы для нахождения первоначальной суммы, срока начисления и величины учетной ставки (формулы 3.51 – 3.55).

 

P = S (1- d _c) ⁿ (3.51)

 

; (3.52)

 

; (3.53)

 

; (3.54)

 

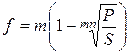. (3.55)

 

 

3.3.6 Принцип эквивалентности процентных ставок

 

Эквивалентные процентные ставки – это процентные ставки разного вида, применение которых при различных начальных условиях дает одинаковые финансовые результаты

Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.

Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности, принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.

Рассмотрим случай, когда все условия финансовой операции совпадают, т. е. первоначальный капитал, временная база, метод расчета (точный или обыкновенный) процентов и период начисления одинаковы.

В противном слу­чае применяются те же рассуждения и преобразования, только полученные формулы будут содержать несколько большее количество переменных.

Приравнивая формулы для определения наращенной суммы при различных способах начисления процентов попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.

Рассмотрим несколько случаев. Приравнивая соотношения (3.7) и (3.22), получим формулы (3.56) и (3.57):

 

; (3.56)

 

. (3.57)

 

Из формул (3.7) и (3.25) получаем формулы (3.58) и (3.59):

 

i=[(1 + i_c)ⁿ - 1]/n (3.58)

 

. (3.59)

 

Приравнивание формул (3.7) и (3.30) дает формулы (3.60) и (3.61):

 

(3.60)

 

(3.61)

 

Для различных случаев сложных процентов, приравнивая формулы (3.25) и (3.30), получаем формулы (3.62) и (3.63),:

 

; (3.62)

 

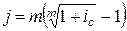. (3.63)

 

Полученная по формуле (3.63), годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов.

Применяется для оценки реальной доходности финансовой операции, или сравнения процентных ставок в случае, когда используются различные интервалы начисления.

Очевидно, что значение эффективной процентной ставки больше значения номинальной, а совпадают они при m = 1.

Из формул (3.25) и (3.44) получаем формулы (3.64) и (3.65):

 

i _c = 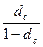; (3.64)

 

d_c = . (3.65)

 

Аналогичным образом получаем зависимости между любыми другими эквивалентными процентными ставками.

Проанализировав полученные формулы, можно сделать выводы:

1. эквивалентность различных процентных ставок никогда не зависит от величины первоначальной суммы Р (для данного рассматриваемого случая, когда первоначальная сумма Р предполагается одинаковой).

2. эквивалентность процентных ставок всегда зависит от продолжительности периода начисления за исключением случая эквивалентности между собой сложных процентных ставок разного вида (если период начисления один и тот же).

Используя для вычислений формулы (3.25) и (3.44), можно построить таблицу, отражающую зависимость между эквивалентными сложными учетными ставками и ставками ссудных процентов (таблица 3.1)

Видно, что небольшие учетные ставки имеют эквивалентные ставки ссудного процента, сопоставимые по величине, но с ростом учетных ставок разница увеличивается.

 

 

Таблица 3.1 – Зависимость между эквивалентными сложными учетными

ставками м ставками ссудных процентов

5% 6% 8% 10% 20% 30% 40% 45%	5,26% 6,4% 8,7% 11% 25% 43% 66,7% 82%	50% 60% 70% 80% 85% 90% 95% 99%	100% 150% 233% 200% 567% 900% 1900% 9900%

 

 

3.3.7 Учет инфляционного обесценения денег в принятии финансовых решений

 

Инфляция характеризуется обесценением национальной валюты (т. е. снижением ее покупательной способности) и общим повышением цен в стране. Очевидно, что в различных случаях влияние инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесценения денежных средств, то заемщик может получить возможность погасить задолженность деньгами сниженной покупательной способности.

При рассчетах используют относительную величину уровня инфляции – темп инфляции (формула 3.66)

 

, (3.66)

где а – уровень инфляции;

ΔS – разница между суммой покупательная способность которой приведена с учетом инфляции и суммой при отсутствии инфляции.

 

При определении суммы, покупательная способность которой с учетом инфляции равна покупательной способности суммы при отсутствии инфляции (S_а) ипользуют формулу (3.67).

S_a = S + DS = S + S_a= SI_и, (3.67)

где I_и – индекс инфляции – показывает во сколько раз Sа больше S (т е во сколько раз в среднем выросли цены) формула (3.68)

I_и = 1 + а. (3.68)

 

Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Повышение индекса инфляции за определенный период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение – на уменьшение ее темпов.

Пусть а - годовой уровень инфляции. Это значит, что через год сумма S'_a будет больше суммы S в (1 + а) раз. По прошествии еще одного года сумма S”_а будет больше суммы S'_a в (1 + а) раз, т. е. больше суммы S в (1 + а)² раз. Через п лет сумма вырастет по отношению к сумме S в (1 + а)" раз. Отсюда видно, что инфляционный рост суммы S при годовом уровне инфляции а - то же самое, что наращение суммы S по сложной годовой ставке процентов а.

Очень важно запомнить данную аналогию со сложным процентом, так как одна из наиболее часто встречающихся ошибок, связанных с расчетом уровня инфляции за некоторый период, связана именно с неучетом данного обстоятельства.

Например, если цены каждый месяц растут на 8%, то за годовой уровень инфляции, принимают 96% (8% × 12 мес.). Такие расчеты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 120%. Между тем, если уровень инфляции составляет 8% в месяц, это значит, что за месяц цены вырастают в (1 + 0,08) раз, а за год – в 2,52 раза (1,08¹²). Значит, годовой индекс инфляции составляет 2,52 – 1 = 1,52, т. е. годовой уровень инфляции достигает 152%. После такого расчета процентная ставка 120% годовых несколько теряет свою значимость.

Рассмотрим различные случаи задания уровня инфляции.

Если известен годовой уровень инфляции a_r, то за период в n лет (при том, что n = n_a+ п_b и n_a - целое число лет, n_b - оставшаяся нецелая часть года) индекс инфляции будет определяться формулой (3.69):

 

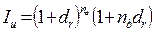(3.69)

 

В некоторых случаях может быть задан уровень инфляции a_m за короткий (меньше года) интервал. Тогда за период, составляющий т таких интервалов индекс инфляции будет определяться по формуле (3.70):

 

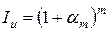(3.70)

 

Теперь можно приложить изложенные выше варианты начисления процентов к условиям инфляционной экономики.

Если в обычном случае первоначальная сумма Р при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму S_a, что требует уже иной процентной ставки – ставки процентов, учитывающей инфляцию.

 

Пусть i_а – ставка ссудного процента, учитывающая инфляцию;

d_а - учетная ставка, учитывающая инфляцию;

j_а - номинальная ставка сложного процента, учитывающая инфляцию;

f_а – номинальная сложная учетная ставка, учитывающая инфляцию;

а – годовой уровень инфляции;

i – простая годовая ставка ссудного процента

Тогда для наращенной суммы S, превращающейся в условиях инфляции в сумму S _а, используем формулу (3.7).

Для данной суммы можно записать еще одно соотношение (формула (3.71), а затем составить уравнение эквивалентности (формула (3.72)

 

S _а=P(1+i)(1+ а) (3.71)

 

(1+i _а)=(1+i)(1+a) (3.72)

 

Таким образом получаем формулу И. Фишера (формула (3.73):

 

I_a= i+ a+ i×a (3.73)

где (а+ i×а) – инфляционная премия величина, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь.

 

Помня формулу И. Фишера, можно избежать еще одной распространенной ошибки. Часто для подсчета процентной ставки, учитывающей инфляцию, к величине реальной ставки доходности просто прибавляют величину темпа инфляции. То есть, если i = 40% и темп инфляции составляет 150%, то за процентную ставку принимается величина i+а = 150+40 = 190%. Но пренебрегать произведением (i×а) можно только в случае небольших значений i и а, при которых оно составляет незначительную величину. В нашем примере это произведение составит 1,5 × 0,4 = 0,6 (60%). Таким образом, ставка доходности, учитывающая инфляцию, в данном случае составила бы 190 + 60 = 250%, и мы рисковали бы потерей почти четвертой части номинальной доходности операции, если бы абстрагировались от (i×а).

Рассмотрим теперь различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период.

Для простых процентных ставок по формуле (3.74):

 

(3.74)

 

 

Для простых учетных ставок по формуле (3.75):

 

(3.75)

 

Для случая сложных процентов используем формулу (3.76):

 

(3.76)

 

Если начисление процентов происходит несколько (т) раз в году, используем формулу (3.77):

 

. (3.77)

 

Для случая сложных учетных ставок используем формулы (3.78) и (3.79):

 

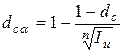; (3.78)

 

(3.79)

 

Используя полученные формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность финансовой операции, и уровень инфляции в течение рассматриваемого периода. Преобразуя формулы (3.74) – (3.79), получаем формулу (3.80):

 

(3.80)

 

Из формулы (3.80) можно сделать следующие выводы:

- если i_ca=a (доходность вложений и уровень инфляции равны), то i_c = 0, т. е. весь доход поглощается инфляцией;

- если i_ca < a (доходность вложений ниже уровня инфля­ции), то i_c < 0, т. с. операция приносит убыток;

- если i_ca > a (доходность вложений выше уровня инфля­ции), то i_c > 0 т. е. происходит реальный прирост вложен­ного капитала.

 

 

3.3.8 Аннуитеты

 

Серия равновеликих платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).

Примером аннуитета могут быть регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам и т.д.

Аннуитеты различаются следующими основными характеристиками:

- величиной каждого отдельного платежа;

- интервалом между каждым отдельным платежом;

- сроком от начала аннуитета до конца его последнего периода (бывают и неограниченные по времени – вечные аннуитеты);

- процентной ставкой, применяемой при наращении платежей.

Введем следующие обозначения:

R - величина каждого отдельного платежа;

i_c - процентная ставка, по которой начисляются проценты;

S_k - наращенная сумма для k-го платежа;

S - наращенная (будущая) сумма всего аннуитета (т. е. сумма всех платежей с процентами);

А_k - современная величина k-го платежа;

А - современная величина всего аннуитета (т. е. сумма современных величин всех платежей);

п - число платежей.

Величины А и S являются основными объектами аннуитетных вычислений.

Рассмотрим аннуитет с ежегодными платежами, на которые начисляются проценты в конце каждого года по сложной процентной ставке i_c.

Сумма S₁ первого платежа с наращенными на него за весь срок процентами(формула (3.81) составит по формуле (3.25):

 

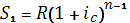(3.81)

 

Сумма второго платежа (проценты на него будут начисляться на один год меньше) будет определяться по формуле (3.82):

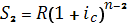(3.82)

На последний платеж, произведенный в конце п-го года, проценты уже не начисляются (формула (3.83):

 

(3.83)

 

 

Тогда для общей наращенной суммы формула (3.84):

 

(3.84)

 

Коэффициент наращения, как можно заметить, представляет собой сумму членов геометрической прогрессии, для которой первый член q₁ равен 1, а знаменатель q – (1+i_c). Используя формулу суммы членов геометрической прогрессии, преобразуем формулу (3.84) в более удобный для вычислений вид (формула (3.85):

 

,(3.85)

 

где к_на - коэффициент наращения (формула 3.86):

 

. (3.86)

 

Определим теперь современное значение А финансовой ренты.

Для каждого платежа его современное значение а_t будет определяться по формуле (3.87):

. (3.87)

 

Современная величина всей ренты, следовательно, будет определяться по формуле (3.88):

 

, (3.88)

где а (коэффициент приведения ренты) - сумма геометрической прогрессии с параметрами .

 

Для а получаем формулу (3.89), а для современной величины А, соответственно формулу (3.90):

 

(3.89)

 

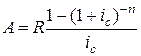. (3.90)

 

Путем преобразований полученных формул (3.89) и (3.90) для определения размера очередного платежа получаем формулы (3.91) и (3.92):

 

; (3.91)

 

. (3.92)

 

Для определения срока ренты (при прочих заданных условиях) получаем формулы (3.93) и (3.94):

 

; (3.93)

 

. (3.94)

 

 

3.3.9 Дивиденды и проценты по ценным бумагам. Доходность операций с ценными бумагами

 

Вложения денежного капитала в различного вида ценные бумаги (долевое участие в предприятиях, займы другим предприятиям под векселя или иные долговые обязательства) – важнейший элемент развивающейся рыночной экономики.

Цель финансовых вложений – получение дохода и (или) сохранение капитала от обесценения в условиях инфляции. Следовательно, необходимо уметь правильно оценивать реальный доход по разному виду ценных бумаг.

Рассмотрим сначала виды существующих в настоящее время ценных бумаг и определим разницу в начислении процентов и возможностях получения дохода по ним.

В зависимости от формы предоставления капитала и способа выплаты дохода ценные бумаги делятся на долговые и долевые.

Долговые ценные бумаги (купонные облигации, сертификаты, векселя) обычно имеют фиксированную процентную ставку и являются обязательством выплатить полную сумму долга с процентами на определенную дату в будущем; по дисконтным облигациям доход представляет собой скидку с номинала.

Долевые ценные бумаги (акции) представляют собой непосредственную долю держателя в реальной собственности и обеспечивают получение дивиденда в неограниченное время.

Все прочие виды ценных бумаг являются производными от долговых либо долевых ценных бумаг и закрепляют право владельца на покупку или продажу акций и долговых обязательств. Это опционы, фьючерсные контракты.

Расчет дохода по различным видам ценных бумаг производится на основе полученных в предыдущих параграфах формул.

При покупке (учете) векселей и других денежных обстоятельств до наступления срока платежа используются учетные ставки. Тогда доход, начисленный по учетной ставке (дисконт), становится доходом лица, купившего вексель, когда наступает срок оплаты. Владелец векселя получает указанную в нем сумму за вычетом дисконта, но зато раньше срока.

При операциях с облигациями источником дохода являются фиксированные проценты (в случае купонных облигаций), а также разность между ценой, по которой облигация приобретается и ценой, по которой она выкупается. Выкупная цена облигации обычно совпадает с ее номиналом.

Существуют облигации без выплаты процентов (дисконтные облигации), инвестирование средств в которые будет доходным только при покупке их со скидкой с номинала, т.е. с дисконтом.

Введем обозначения:

N – номинальная стоимость облигации;

P_o – цена покупки облигации;

I_o – доход по облигации;

n – период, за который начисляются проценты;

i – процентная ставка;

i_c - эффективная ставка сложных процентов.

При расчетах дохода используют понятие курса облигации Р_к формула (3.95):

. (3.95)

 

Тогда доход по облигации будет определяться по формуле (3.96) или (3.97):

 

. (3.96)

 

. (3.97)

 

 

При измерении доходности через эффективную ставку сложных процентов получаем формулу (3.98):

 

(3.98)

 

При покупке акций источником дохода могут быть дивиденды и разница между ценой приобретения и ценой продажи.

Фиксированные дивиденды (определенный процент от номинальной стоимости акции) выплачиваются по привилегированным акциям.

Введем обозначения:

P_a – цена приобретения акции;

Q – цена продажи акции;

N – номинальная цена акции;

F – величина дивидендов;

I_F – доход от дивидендов;

I_a - общий доход от покупки акции;

n – срок в годах от момента покупки до момента продажи.

 

Общий доход от покупки акции будет определяться формулой (3.99):

 

. (3.99)

 

Если дивиденды вновь не реинвестируются, доход от них будет определяться по формуле (3.100):

 

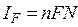. (3.100)

 

Величина дивидендов по простым акциям устанавливается общим собранием акционеров в зависимости от финансовых результатов года (дивиденды могут и не выплачиваться, если прибыли нет или она целиком направляется на развитие), поэтому расчет дохода от таких акций может быть только ориентировочным и производится по выражениям (3.99) и (3.100).

Для расчета доходности покупки акции в виде эффективной ставки сложных процентов применяется формула (3.101):

 

. (3.101)

 

3.3.10 Банковские операции. Финансовый кредит.

 

Привлеченные средства банка формируются: 1) за счет привлечения кредитов и займов, полученных от других юридических лиц, 2) в ходе депозитных операций.

Депозитные операции – это операции банков по привлечению денежных средств юридических и физических лиц во вклады на определенный срок либо до востребования. Объектами депозитных операций являются депозиты – суммы денежных средств, которые субъекты депозитных операций вносят в банк, на определенное время оседающие на счетах в банке в силу действующего порядка осуществления банковских операций.

Ключевым элементом финансовой системы любого развитого государства сегодня является Центральный Банк. Центральный банк Российской Федерации занимает особое положение среди всех юридических лиц, занятых управлением или хозяйственной деятельностью. С одной стороны, он представляет собой орган государственного управления; с другой стороны – Центральный банк выступает как коммерческий банк, хотя получение прибыли не служит целью деятельности Центрального банка РФ.

Кредитная экспансия ЦБ РФ увеличивает кредитные ресурсы коммерческих банков, которые в результате выдаваемых кредитов повышают общую массу денег в обращении. Кредитная рестрикция влечет за собой ограничения возможностей коммерческих банков по выдаче кредитов и тем самым по насыщению экономики деньгами. Инструментами кредитной экспансии или кредитной рестрикции являются: официальная учетная ставка Центрального банка; некоторые неэкономические меры.

Официальная учетная ставка – это проценты по ссудам, используемым Центральным банком при кредитовании коммерческих банков. Определение размеров учетной ставки – один из наиболее важных аспектов кредитно-денежной политики, а изменение учетной ставки выступает показателем изменений в области кредитно-денежного регулирования. Размер учетной ставки обычно зависит от уровня ожидаемой инфляции и в то же время оказывает на инфляцию большое влияние.

Рефинансирование банков. Под рефинансированием банков понимается предоставление Центральным банком РФ кредита коммерческим банкам. Рефинансирование осуществляется путем проведения кредитных аукционов и представления ломбардного кредита. Кредитные аукционы проводятся в форме удовлетворения аукционных заявок коммерческих банков с частотой и в сроки, определяемые ЦБ РФ, исходя из задач денежно-кредитной политики.

Ломбардный кредит – это форма рефинансирования, при которой ЦБ РФ предоставляет ссуды под залог. Предметом залога выступают в первую очередь надежные ценные бумаги. Предоставление ломбардного кредита может производиться как путем удовлетворения заявок банка по фиксированной ломбардной процентной ставке, так и через проведение аукциона заявок банков по сложившейся на аукционе ставке отсечения. Договор на предоставление банку ломбардного кредита не пролонгируется.

При выдаче ломбардного кредита по фиксированной процентной ставке используется ломбардная ставка ЦБ РФ, установленная Советом директоров ЦБ РФ и действующая на дату заключения договора.

В срок, установленный договором на предоставление ломбардного кредита, банк осуществляет возврат кредита и уплату процентов по нему. Банк может досрочно погасить ломбардный кредит полностью или частично. После погашения кредита, включая проценты по нему, ЦБ РФ возвращает банку заложенные ценные бумаги.

Кредиты банков могут выдаваться как в рублях, так и в валюте, причем на коммерческих условиях с начислением повышенных процентов за не погашенную в срок часть задолженности по кредиту. Плата за кредит взимается по ставкам, сложившимся на денежном рынке по краткосрочным кредитам, и на рынке капитала – по долгосрочным кредитам. Процентные ставки по кредитам обычно определяются банком как договорные по соглашению с заемщиком; они устанавливаются на период, обусловленный кредитным договором. Могут применяться следующие методы взимания процентов: процент удерживается в момент предоставления кредита, в момент погашения кредита или равномерными взносами на протяжении всего срока кредита. Заемщик возмещает банку уплаченную им банковскую комиссию, а также телеграфные и другие расходы, связанные с использованием кредита. Проценты за кредит начисляются с момента фактического его использования.

Кредит представляет собой форму движения денежного капитала и обеспечивает превращение собственного капитала кредитора в заемный капитал заемщика.

Денежные кредиты бывают:

- инвестиционный налоговый;

- налоговый;

- финансовый;

- коммерческий.

Финансовый кредит – прямая выдача кредитором денег заемщику. Различают следующие формы предоставления кредита заемщику:

- срочный кредит;

- контокоррентный кредит;

- онкольный кредит;

- ипотечный кредит;

- ломбардный кредит.

Ипотечный кредит – кредит под залог недвижимости. Выдается ипотечными банками для покрытия крупных капитальных затрат, нового строительства; приобретения недвижимости. Объект строительства является предметом залога.

В процессе ипотечного кредитования анализируют состояние и эффективность использования кредита. Анализ проводится как традиционным способом, так и с использованием финансовых коэффициентов, которые включают расчет коэффициента ипотечной задолженности и ипотечной постоянной.

Коэффициент ипотечной задолженности показывает долю ипотечного долга (т. е. заемных средств) в общей стоимости недвижимости формула (3.102):

 

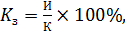(3.102)

где К₃ — коэффициент ипотечной задолженности, %;

И — сумма ипотечного кредита, руб.;

К — общая стоимость недвижимости, руб.

 

Чем выше значение данного коэффициента, тем выше доля заемных средств и, следовательно, ниже доля собственных средств инвестора в финансировании сделки с недвижимостью. С позиции кредитора более высокий коэффициент ипотечной задолженности означает более высокую степень риска нарушения заемщиком своих обязательств и лишения его права выкупа заложенной недвижимости.

Ипотечная постоянная — это процентное соотношение ежегодных платежей по обслуживанию долга и основной суммы ипотечного кредита формула (3.103):

 

П₁= 100%, (3.103)

где П₁ — ипотечная постоянная, %;

И — сумма ипотечного кредита, руб.;

Д — годовая сумма платежей по обслуживанию долга, руб.

 

Для того чтобы ипотечный кредит был полностью погашен, ипотечная постоянная должна быть выше номинальной ставки процента за кредит. Превышение ипотечной постоянной над процентной ставкой обеспечивает выплату основной суммы кредита. Если же ипотечная постоянная равна процентной ставке, то погашение первоначальной суммы кредита произойдет «шаровым» платежом. «Шаровой» платеж означает, что по кредитному договору заемщик регулярно выплачивает только проценты, а основная сумма долга выплачивается по окончании срока договора. Это заставляет заемщика принимать меры к накоплению денег для выплаты сразу большой суммы платежа. Когда же ипотечная постоянная меньше размера процентной ставки, то выплаты по кредиту не покроют даже проценты по нему. В этом случае невыплаченная часть процентов будет накапливаться вместе с основной суммой ипотечного долга, и его остаток будет расти.

Следующим видом денежного кредита является коммерческий кредит. Коммерческие кредиты – это расчеты с рассрочкой или отсрочкой платежа одного хозяйствующего субъекта или предпринимателя с другим хозяйствующим субъектом (предпринимателем). Этот вид кредита называют также кредитом поставщика.

Основными формами кредита как разновидности расчетов (расчетов с рассрочкой платежа) являются:

- фирменный кредит;

- вексельный (учетный) кредит;

- факторинг;

- овердрафт.

Фирменный кредит – традиционная форма кредитования, при которой поставщик (продавец) предоставляет кредит покупателю в форме отсрочки платежа. Разновидностью фирменного кредита является предоставление отсрочки платежа при покупке с одновременным получением аванса от покупателя.

Факторинг (англ, factor – посредник) – это разновидность торгово-комиссионной операции, связанной с кредитованием оборотных средств. Факторинг представляет собой инкассирование дебиторской задолженности покупателя и является специфической разновидностью краткосрочного кредитования и посреднической деятельности.

По договору финансирования под уступку денежного требования одна сторона (финансовый агент) передает или обязуется передать другой стороне (клиенту) денежные средства в счет денежного требования клиента (кредитора) к третьему лицу (должнику), вытекающего из предоставления клиентом товаров, выполнения им работ или оказания услуг третьему лицу, а клиент уступает или обязуется уступить финансовому агенту это денежное требование (ст. 824 ГК РФ).

Должник обязан произвести платеж финансовому агенту при условии, что он получил от клиента либо от финансового агента письменное уведомление об уступке денежного требования данному финансовому агенту и в уведомлении определено подлежащее исполнению денежное требование, а также указан финансовый агент, которому должен быть произведен платеж.

Факторинг осуществляется следующим образом. Банк приобретает у хозяйствующего субъекта-продавца право на взыскание дебиторской задолженности покупателя продукции (работ, услуг) и в течение 2-3 дней перечисляет хозяйствующему субъекту 70–90% суммы средств за отгруженную продукцию в момент предъявления платежных документов. После получения платежа по этим счетам от покупателей банк перечисляет хозяйствующему субъекту оставшиеся 30–10% суммы счетов за вычетом процентов и комиссионных вознаграждений.

Стоимость факторингового обслуживания зависит от вида услуг, финансового положения клиента и т. п. При определении платы за факторинг следует исходить из принятого сторонами процента за кредит и среднего срока пребывания средств в расчетах с покупателем.

Пример. Ставка за кредит – 42% годовых. Средний срок оборачиваемости средств в расчетах с покупателем – 14 дн. Плата за эти операции составит: 42 x14 / 360 = 1,63% суммы, принятой к оплате факторинга. За оплату продавцу документов на сумму 2000 руб. фактор получает от него: 1,63 х 2000 = 32,6 руб. При помещении документа продавца в картотеку покупателя вся сумма пени также является доходом фактора. В случае задержки в оплате на 10 дней пени от покупателя (0,03%) перечисляются фактору в сумме 6 руб. [(0,03 х 10 х 2000): 100].

Овердрафт – это форма краткосрочного кредита, предоставление которого осуществляется путем списания банком средств по счету клиента сверх остатка на его счете. В результате такой операции образуется отрицательный баланс, т. е. дебетовое сальдо – задолженность клиента банку. Банк и клиент заключают между собой соглашение, в котором устанавливаются максимальная сумма овердрафта, условия предоставления кредита, порядок погашения его, размер процента за кредит.

Использование предприятием для экономической деятельности не только собственных средств, но и заемных повышает рентабельность инвестирования собственных средств.

Увеличение рентабельности собственных средств называется финансовым левериджем (финансовым рычагом, эффектом финансового рычага).

Формулу для определения рентабельности собственных средств с учетом финансового рычага можно получить следующим образом.

Если в инвестициях наряду с суммой собственных средств (СС) используется сумма заемных средств (ЗС), прибыль от инвестиций (ПР) можно записать в виде формулы (3.104):

 

ПР = ЭР х (СС + ЗС), (3.104)

где ЭР — экономическая рентабельность.

 

Сумма процентов (П), выплаченных за использование заемных средств по ставке процентов (СП), будет определяться по формуле (3.105):

 

П = СП х ЗС (3.105)

 

Сумма прибыли, облагаемая налогом, будет определяться по формуле (3.106):

 

ПРН = ПР – П = ПР – СП х ЗС (3.106)

 

 

При ставке налога СН сумма налога (Н) будет определяться по формуле (3.107):

 

Н = ПРН х СН (3.107)

 

Тогда чистая прибыль определится по формуле (3.108):

 

ЧП = ПРИ – Н = ПРН – ПРН х СН = ПРН х (1 – СН) =

= (ПР – СП х ЗС) х (1 – СН) = (ЭР х (СС + ЗС) х (1 – СН) = (3.108)

= (ЭР х СС + ЗС х (ЭР – СП)) х (1 – СН).

 

Разделив это выражение на сумму инвестированных собственных средств, получаем формулу для их рентабельности (3.109):

 

РСС = ЧП / СС = [(1 – СН) х ЭР] + [(1 – СН)х(ЭР – СП) х ЗС/СС], (3.109)

где [(1 – СН)х(ЭР – СП) х ЗС/СС] – «эффект финансового рычага» (ЭФР) при использовании заемных средств (ЗС>0).

 

Разность между экономической рентабельностью и ставкой процентов по займу называют «дифференциалом финансового рычага» (ДФР) (формула (3.110):

ДФР = ЭР – СП (3.110)

 

Соотношение заемных и собственных средств называют «плечом финансового рычага» (ПФР) (формула (3.111):

 

ПФР = ЗС/СС (3.111)

 

Таким образом, «эффект финансового рычага» может быть представлен в виде формулы (3.112):

 

ЭФР = (1 – СН) х ДФР х ПФР (3.112)

 

Эффект финансового рычага будет тем больше, чем больше будет экономическая рентабельность инвестиций по сравнению со ставкой процентов по займу и чем больше будет соотношение заемных и собственных средств.

Помимо обеспечения эффективного использования кредита (повышение эффективности собственных средств) важным вопросом является способ погашения кредита. Погашение кредита может осуществляться равными долями, разовым платежом и т. д.

Равная сумма выплат по периодам за кредит может быть определена по формуле (3.113):

 

P = (K × r) / (1 – (1 – r)^-n), (3.113)

 

где Р — равная сумма выплат по периодам, руб.;

К — размер кредита, руб.;

г — процентная ставка за один период;

n — число периодов (месяцев, кварталов, лет).

 

Общая сумма платежа за кредит S в этом случае определяется по формуле (3.114):

 

S = P × n (3.114)

 

Плата за кредит, т. е. общая сумма процентов, которые должен выплатить заемщик кредитору в случае разового погашения кредита, рассчитывается по формуле (3.115):

I = K × r × n, (3.115)

где I – общая сумма процентов за кредит, руб.;

К – сумма кредита, руб,

r – годовой процент,

n – количество лет.

 

Тогда общая сумма платежа за кредит в случае разового погашения кредита будет определяться по формуле (3.116):

 

S