ВВЕДЕНИЕ
Методические указания предназначены для студентов дневного и вечернего отделения факультета №14 специальностей 150601.65, 160301.65, 220301.65, 230102.65. Указания выделяют основные понятия темы и определяют последовательность изучения материала.
ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ
Одним из недостатков классического определения вероятности, ограничивающим его применение, является то, что его нельзя применить к испытаниям с бесконечным числом исходов. По классической схеме испытания число возможных исходов испытания должно быть конечным. Этот недостаток можно преодолеть, если ввести понятие геометрического определения вероятности.
Рассмотрим геометрическую схему испытания: результат испытания определяется случайным положением точки в некоторой области, причем любые положения точек в этой области равновозможны. Геометрическая вероятность тогда определяется как вероятность попадания точки в некоторую область: одномерную (например, отрезок прямой, длина дуги и т.п.), двумерную (площадь некоторой фигуры) или трехмерную (объем некоторого тела в пространстве).
Геометрической вероятностью события А называется отношение меры (размера) области, благоприятствующей появлению события А, к мере (размеру) всей области:
где G – размер (длина, площадь или объем) всей области, G0 – размер той части области, попадание в которую благоприятствует данному событию.
ПРИМЕР 1. На отрезке длиной40 см помещен отрезок длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок.
Решение. Вероятность попадания точки на меньший отрезок пропорциональна длине этого отрезка и не зависит от его расположения относительно большого отрезка. Тогда:
ПРИМЕР 2. В квадрат вписан круг радиусом r. Найти вероятность того, что точка, брошенная наудачу в квадрат, окажется внутри круга.
Решение. Площадь квадрата S =4 r 2; площадь круга S0 =π r 2. Тогда:
ПРИМЕР 3. Два друга условились встретиться в определенном месте, договорившись только о том, что каждый является туда в любой момент времени между 11 и 12 ч. и ждет в течение 30 мин. Если один из них к этому времени еще не пришел или уже успел уйти, то встреча не состоится. Найти вероятность того, что встреча состоится.
Решение. Введем в рассмотрение прямоугольную систему координат. Обозначим моменты прихода двух друзей через х и у. По условию: 
или 
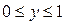(если за начало отсчета взять 11 ч.). Этим неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OKLM со стороной, равной 1 (рис.1).
|
Рис. 1. Геометрическая схема встречи
Событие С – «встреча друзей состоится» – можно представить в виде точки, брошенной на квадрат OKLM. Оно произойдет, если разность между х и у не превзойдет 0,5 ч (по абсолютной величине), т.е.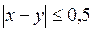 
или 
На рис. 1 этому неравенству соответствует полоса, обозначенная через g.
Площадь квадрата G равна SG =1,0. Площадь полосы g равна Sg =1- 2(1/2)·0,52=0,75 или Sg =1-0,52=0,75.
Тогда:
ЗАДАЧИ
1. На отрезке длиной 20 см помещен меньший отрезок длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Отв. 1/2.
2. В течение промежутка времени от 11 ч. до 11ч. 30 мин. должен быть телефонный звонок. Какова вероятность того, что звонок последует в последние 10 мин. Отв. 1/3.
3. Диск разделен на 12 секторов, попеременно окрашенных в черный, белый и синий цвет. По диску произведен выстрел. Найти вероятность, что пуля попадет в один из белых секторов. Отв. 1/3.
4. В круг радиусом R помещен меньший круг радиусом r. Найти вероятность того, что точка, поставленная наудачу в большой круг, попадет также и в малый круг. Отв. r 2/ R 2.
5. На плоскости начерчены две концентрические окружности с одним центром и радиусами 5 см и 10 см. Найти вероятность того, что точка, брошенная на удачу в большой круг, попадет также и в кольцо, образованное окружностями. Отв. 0,75.
6. Внутрь круга радиусом R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг: а) квадрата со стороной а; б) равностороннего треугольника со стороной а. Отв. а) а 2/ πR 2; б) а 3/4 πR 3.
7. Два студента договорились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение ¼ часа, после чего уходит. Найти вероятность, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода в промежутке от 12 до 13 часов. Отв. 7/16.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте классическое определение вероятности события. В чем состоит его недостаток?
2. Сформулируйте геометрическое определение вероятности события.
ЛИТЕРАТУРА
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001. – 479 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2001. – 400 с.
ОГЛАВЛЕНИЕ
Введение………………………………………………............. 3
1. Геометрическое определение вероятности события …………3
2. Задачи..………………...………………………………………. 6
3. Контрольные вопросы…………………………………………. 7
Литература.………………………………………………………7
Юлия Борисовна Егорова
Игорь Михайлович Мамонов
Татьяна Анатольевна Никулина
ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ
Методические указания к практическим занятиям
по курсу «Высшая математика»
Ведущий редактор О.В. Филиппова
Подп. в печать
Усл.печ.л. 0,5 п.л. Уч.-изд.л. 0,33
Формат 60х84/16.
Тираж 30 экз. Зак. №6
Издательско-типографский центр МАТИ
109240 Москва, Берниковская наб., 14
