Практикум по математическому анализу
Тема. Производные функций
- основные правила дифференцирования;
- дифференцирование сложной функции;
- производная функции, заданной неявно;
- производная параметрически заданной функции.
Основные правила дифференцирования
1.  , где
, где  – постоянное число (константа).
– постоянное число (константа).
2. 
3. 
4. 
5. Производная сложной функции – см. далее.
Дифференцирование сложной функции
u(v(x)). Здесь две функции –  и
и  , причем функция
, причем функция  , образно говоря, вложена в функцию
, образно говоря, вложена в функцию  . Функция такого вида (когда одна функция вложена в другую) называется сложной функцией.
. Функция такого вида (когда одна функция вложена в другую) называется сложной функцией.
Функция  образно будет называться внешней функцией, а функция
образно будет называться внешней функцией, а функция  – внутренней (или вложенной) функцией.
– внутренней (или вложенной) функцией.
Пример сложной функции: 
Правило дифференцирования сложной функции  .
.
Таблица нахождения производных сложных функций
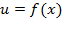
| 
|

| |

| 
|

| 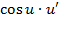
|

| 
|
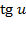
| 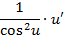
|
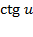
| 
|

| 
|

| 
|

| 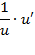
|

| 
|
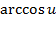
| 
|
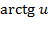
| 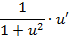
|

| 
|
Пример 1
Найти производную функции 
Первый шаг, который нужно выполнить при нахождении производной сложной функции, состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде  понятно, что под синус вложен многочлен
понятно, что под синус вложен многочлен 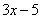 .
.
А если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого существует следующий прием.
Представим, что нам нужно вычислить значение выражения  при
при 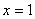 (вместо единицы может быть любое число).
(вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие:  , поэтому многочлен
, поэтому многочлен 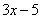 и будет внутренней функцией
и будет внутренней функцией  :
:

Во вторую очередь нужно будет найти  , поэтому синус – будет внешней функцией:
, поэтому синус – будет внешней функцией:

Теперь самое время применить правило дифференцирования сложной функции  .
.

Сначала находим производную внешней функции  (синуса).
(синуса).

Обратите внимание, что внутренняя функция  не изменилась, её мы не трогаем.
не изменилась, её мы не трогаем.
Далее 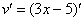
Результат применения формулы  выглядит так:
выглядит так:
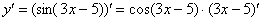
Далее мы берем производную внутренней функции:

Постоянный множитель обычно выносят в начало выражения:

Пример 2
Найти производную функции 
Решение:

Разбираемся, где внешняя функция, а где внутренняя. Для этого пробуем вычислить значение выражения  при
при 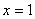 . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:
. Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:  , значит, многочлен
, значит, многочлен  – и есть внутренняя функция:
– и есть внутренняя функция:

И, только потом выполняется возведение в степень  , следовательно, степенная функция – это внешняя функция:
, следовательно, степенная функция – это внешняя функция:

Согласно формуле  , сначала нужно найти производную от внешней функции, в данном случае, от степени. Таким образом, результат применения правила дифференцирования сложной функции
, сначала нужно найти производную от внешней функции, в данном случае, от степени. Таким образом, результат применения правила дифференцирования сложной функции  следующий:
следующий:

При взятии производной от внешней функции  , внутренняя функция
, внутренняя функция  не меняется:
не меняется:
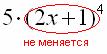
Теперь осталось найти производную от внутренней функции и преобразовать результат:

Пример 3
а) Найти производную функции 

б) Найти производную функции 
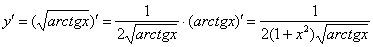
Пример 4
Найти производную функции 
Для того, чтобы продифференцировать корень, его нужно представить в виде степени  . Таким образом, сначала приводим функцию в подходящий для дифференцирования вид:
. Таким образом, сначала приводим функцию в подходящий для дифференцирования вид:
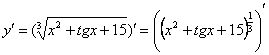
Сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции  :
:

Степень можно снова представить в виде радикала (корня), а для производной внутренней функции применить правило дифференцирования суммы:

Пример 5
Найти производную функции 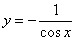
Необходимо подготовить функцию для дифференцирования – вынести минус за знак производной, косинус поднять в числитель:

Косинус – внутренняя функция, возведение в степень – внешняя функция.
По правилу:

Находим производную внутренней функции, косинус сбрасываем обратно вниз:
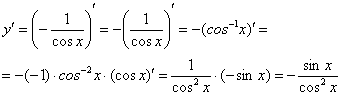
Пример 6
Найти производную функции 
Разбираемся во вложениях этой функции. Пробуем вычислить выражение  с помощью значения
с помощью значения 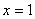 . Сначала нужно найти
. Сначала нужно найти  , значит, арксинус – самое глубокое вложение:
, значит, арксинус – самое глубокое вложение:

Затем этот арксинус единицы следует возвести в квадрат  :
:

И, наконец, семерку возводим в степень  :
:

То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
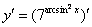
Согласно правилу  сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции:
сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции:  Единственное отличие – вместо «икс» у нас сложное выражение
Единственное отличие – вместо «икс» у нас сложное выражение  , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции
, что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции  следующий:
следующий:

Под штрихом снова сложная функция. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени:


Пример 7
Найти производную функции 

Сначала используем правило дифференцирования суммы  , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу
, заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу  :
:

В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило  :
:

Замечаем, что под некоторыми штрихами у нас находятся сложные функции  ,
, 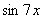 .
.

Производная функции, заданной неявно
Функция одной переменной 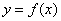 –это правило, по которому каждому значению независимой переменной
–это правило, по которому каждому значению независимой переменной 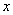 соответствует одно и только одно значение функции
соответствует одно и только одно значение функции  .
.
Переменная 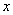 называется независимой переменной или аргументом.
называется независимой переменной или аргументом.
Переменная  называется зависимой переменной или функцией.
называется зависимой переменной или функцией.
Рассмотрим функцию 
Мы видим, что слева у нас одинокий «игрек» (функция), а справа – только «иксы». То есть, функция  в явном виде выражена через независимую переменную
в явном виде выражена через независимую переменную 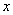 .
.
Рассмотрим другую функцию: 
Здесь переменные 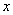 и
и  расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др.
расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др.
 – пример неявной функции.
– пример неявной функции.
Пример 1
Найти производную от функции, заданной неявно 
1) На первом этапе навешиваем штрихи на обе части:

2) Используем правила линейности производной:

3) Непосредственное дифференцирование.
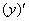 – производная от функции равна её производной:
– производная от функции равна её производной:  .
.
Как дифференцировать 
Здесь сложная функция. Потому что буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (см. определение в начале пункта). Таким образом, синус – внешняя функция,  – внутренняя функция. Используем правило дифференцирования сложной функции
– внутренняя функция. Используем правило дифференцирования сложной функции  :
:
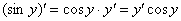
Произведение дифференцируем по обычному правилу  :
:
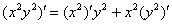
Обратите внимание, что  – тоже сложная функция:
– тоже сложная функция:

Само оформление решения должно выглядеть примерно так:


Если есть скобки, то раскрываем их:
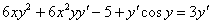
4) В левой части собираем слагаемые, в которых есть «игрек» со штрихом. В правую часть – переносим всё остальное:

5) В левой части выносим производную  за скобки:
за скобки:

6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:

Пример 2
Найти производную от функции, заданной неявно 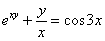
Заключаем обе части под штрихи и используем правило линейности:


Дифференцируем, используя правило дифференцирования сложной функции  и правило дифференцирования частного
и правило дифференцирования частного  :
:

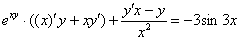
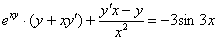
Раскрываем скобки:

Теперь нам нужно избавиться от дроби. В знаменателе дроби находится  . Умножаем каждое слагаемое каждой части на
. Умножаем каждое слагаемое каждой части на  . Если подробно, то выглядеть это будет так:
. Если подробно, то выглядеть это будет так:

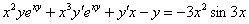
Иногда после дифференцирования появляется 2-3 дроби. Если бы у нас была еще одна дробь, например,  , то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на
, то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на 
Далее алгоритм работает стандартно, после того, как все скобки раскрыты, все дроби устранены, слагаемые, где есть «игрек штрих» собираем в левой части, а в правую часть переносим всё остальное:

В левой части выносим  за скобку:
за скобку:

Окончательный ответ:
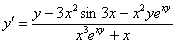
Пример 3
Найти производную от функции, заданной неявно 
Навешиваем штрихи на обе части:

Используем правила линейности:

Находим производные:


Раскрываем все скобки:

Переносим все слагаемые с  в левую часть, остальные – в правую часть:
в левую часть, остальные – в правую часть:

В левой части выносим  за скобку:
за скобку:

Окончательный ответ:

Пример 4
Найти производную от функции, заданной неявно 
Решение:






Таким образом: 






