$$ векторной сумме всех сил системы
$ нулю
$ сумме квадратов всех сил системы
$ алгебраической сумме всех сил системы
Отличие равнодействующей силы от уравновешивающей силы
$$ равнодействующая сила эквивалентна действию заданной системы сил, а уравновешивающая сила равна по модулю равнодействующей, но противоположно ей направлена
$ равнодействующая сила и уравновешивающая сила равны по модулю и направлены в одну сторону
$ они отличаются и по модулю, и по направлению
$ модули и направления равнодействующей и уравновешивающей сил не зависят друг от друга
В каком случае величина и знак главного момента не зависят от центра приведения?
$$ когда главный вектор равен нулю, а главный момент не равен нулю
$ когда главный вектор и главный момент не равны нулю
$ когда главный вектор не равен нулю, а главный момент равен нулю
$ когда главный вектор и главный момент равны нулю
Формулы для определения аналитическим путем моментов сил относительно координатных осей
$$ 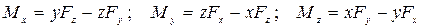
$ 
$ 
$ 
Моментом силы относительно точки называется
$$ произведение модуля силы на кратчайшее расстояние от линии действия силы до точки
$ алгебраическая величина, равная произведению проекций силы на плоскость, перпендикулярную этой оси, на расстояние от точки пересечения оси с плоскостью до линии действия проекции силы
$ произведение модуля силы на расстояние от конца вектора силы до точки
$ удвоенное произведение модуля силы на кратчайшее расстояние от линии действия силы до точки
Проекцией силы на ось называется
$$ произведение модуля силы на косинус угла между линией действия силы и положительным направлением оси
$ алгебраическая величина, равная произведению проекций силы на плоскость, перпендикулярную этой оси, на расстояние от точки пересечения оси с плоскостью до линии действия проекции силы
$ произведение модуля силы на расстояние от конца вектора силы до точки
$ произведение модуля силы на кратчайшее расстояние от линии действия силы до точки
Моментом силы относительно оси называется
$$ алгебраическая величина, равная произведению проекций силы на плоскость, перпендикулярную этой оси, на расстояние от точки пересечения оси с плоскостью до линии действия проекции силы
$ произведение модуля силы на косинус угла между линией действия силы и положительным направлением оси
$ произведение модуля силы на расстояние от конца вектора силы до точки
$ произведение модуля силы на кратчайшее расстояние от линии действия силы до точки
Моментом пары называется
$$ произведение модуля одной из сил на ее плечо
$ произведение модуля силы на расстояние между точками приложения сил
$ произведение модуля силы на расстояние между концами сил
$ произведение модуля силы на расстояние от линии действия одной силы до точки приложения другой силы
$$$77. Интенсивность есть сила,
$$ приходящаяся на единицу длины нагруженного участка
$ сосредоточенная
$ уравновешивающая
$ равнодействующая






