МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ ПРЕПОДАВАТЕЛЯ
по дисциплине « Биология »
для специальности 060101 – Лечебное дело (очная форма обучения)
К ПРАКТИЧЕСКОМУ ЗАНЯТИЮ № 11
ТЕМА: «Изменчивость и ее формы. Фенотипическая изменчивость»
Аннотация (краткое содержание темы)
Фенотипическая изменчивость
 | |||||
| |||||
| |||||
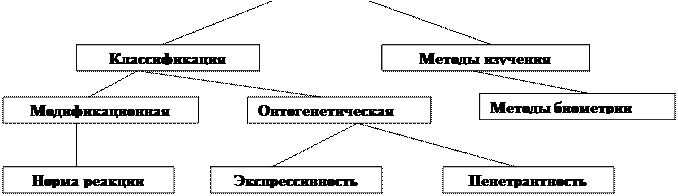
Фенотипическая изменчивость – это ненаследственная изменчивость, которая не затрагивает генотип и не передаётся по наследству. Различают: модификационную и онтогенетическую (эпигенетическую).
Модификационная изменчивость зависит от факторов внешней среды и от нормы реакции (пределов модификационной изменчивости).
Онтогенетическая (эпигенетическая изменчивость) - характеризуетсяразличными модификациями фенотипа эукариотов на разных стадиях онтогенеза.Возникает в результате активации или инактивации определённых групп генов. Изменение активности генов может быть вызвано компактизацией хромосом за счёт связывания ДНК с белками гистонами и образования гетерохроматина; метилированием ДНК. Метилирование – это временная химическая модификация нуклеотидной последовательности без нарушения структуры ДНК. Метилирование осуществляется чаще всего за счёт присоединения метильной группы к цитозину. Катализируется ферментом ДНК-метилтрансферазой. Рисунок распределения метилированных остатков цитозина при репликации сохраняется. Такой специфический рисунок метилирования называется геномным импринтингом.Метилирование может сопровождаться: инактивацией гена; способствует привлечению к району промотора белков, подавляющих транскрипцию; препятствует взаимодействию ДНК с белками репрессорами. Например, метилирование интрона может привести к активности гена.
Экспрессивность – степень выраженности признака. Зависит от внешних условий.
Пенетрантность – пробивание гена в признак. Показывает отношение количества случаев проявления гена к общему количеству носителей этого гена. Выражается в %.
Биомедицинская статистика (биометрия ) – область научного знания, целью которого является планирование и анализ результатов количественных биологических и медицинских экспериментов и наблюдений методами математической статистики.
Генеральная совокупность– этовсе множество, изучаемых объектов определенной категории. Статистические показатели, характеризующие её, называются генеральными параметрами: М – средняя арифметическая, σ – среднее квадратическое отклонение.
Выборочная совокупность (выборка) – это часть генеральной совокупности, отобранной для её оценки.Характеризуется: выборочными параметрами:
– средней арифметической;
S (σ) –средним квадратическим отклонением (стандартное отклонение);
D(x)- дисперсией;
S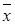 
-ошибкой средней арифметической.
Репрезентативность (представительность) – это свойство выборки достаточно полно характеризовать генеральную совокупность. Выборка считается репрезентативной, если каждый объект выборки отобран случайно из генеральной совокупности. Как генеральная, так и выборочные совокупности характеризуются одинаковыми закономерностями.
Варианта (Хi)– каждый элемент выборки;
Частота встречаемости (mi)– число наблюдений варианты.
Статистическое распределение- совокупность вариант (Хi) и соответствующих им частот (mi).
Распределение может быть нескольких видов. В медико - иологических исследованиях часто встречается нормальное распределение.
Нормальное распределение возникает, когда на изменение случайных величин действуют множество факторов, каждый из которых не имеет преобладающего значения.
Для нормального закона характерны следующие свойства: среднее арифметическое случайной величины является центром распределения и наиболее вероятным значением; изменение среднего арифметического (математического ожидания) не влияет на форму кривой, а только вызывает её смещение по оси Х; параметр σ характеризует изменчивость случайной величины (меру растянутости кривой вдоль оси Х. Чем больше σ,тем более растянута кривая).
Вариационный ряд – это сгруппированные варианты в классах (Х) по их частотам m в возрастающем или убывающем порядке. Вариационные ряды бывают двух видов: безинтервальный и интервальный. Вариационный ряд может быть представлен в виде таблицы или графика. Безинтервальный вариационный рядстроят, если изменчивость относительно невелика.
| классы | ||||||||
| варианты | ||||||||
| частота |
Наиболее распространённым способом изображения вариационного ряда является вариационная кривая или полигон.
На оси абсцисс (Х) откладывается значение класса, а на оси ординат (У) - значения частоты вариант.
Полигон
Интервальный вариационный ряд строят, если изменчивость достаточно велика и величины группируют в классы с определенным интервалом. Например: распределение студентов первого курса по возрасту. Полученные значения распределяем по классам с интервалом = 3, (Dxi =3) Для определения середины класса необходимо сумму крайних вариант класса разделить пополам. Например: 1-й класс 15+18 / 2 = 16,5
| классы | |||||
| Варианты Середина класса | 15-18 (16,5) | 18-21 (19,5) | 21-24 (22,5) | 24-27 (25,5) | 27-30 (28,5) |
| частота |
Интервальный вариационный ряд изображается с помощью гистограммы
Для вариационного ряда, подчиняющегося закону нормального распределения, используются параметрические методы статистического анализа.
Статистические параметры разделяются на две основные группы: средние величины и показатели, характеризующие степень вариации.
Средние величины:
1) Средняя арифметическая величина выборки ()
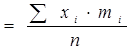
Хi – варианта; Σ – сумма вариант; mi – частота вариант; n – число всех вариант выборки.
2) Мода (Мо) – величина, которая встречается с наибольшей частотой. Она является типичной для всей совокупности. Класс, в котором находится мода, называется модальным.
3) Медиана (Ме) – значение варианты, находящейся точно в середине ряда, при нечётном числе вариант. При чётном числе вариант надо взять значения двух соседних срединных вариант и разделить их сумму на 2. Медиана разделяет всю группу на две равные части: одна имеет значение не больше, чем медиана, а другая – больше.
Показатели вариации:
1) Дисперсия D(x) – характеризуетстепень изменения признака и отклонение его от средней арифметической. D(x) = σ2
D(x) =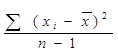 
при n< 30 
при n ≥ 30
2) Среднее квадратическое отклонение или стандартное отклонение – выражает меру изменчивости изучаемого признака. Позволяет определить величину колебаний значений вариант по отношению к средней арифметической.
Определяется среднее квадратическое отклонение по формуле:
при n ≥ 30 
при n< 30σ =√ 
3) Коэффициент вариации (СV) – является одним из показателей разнообразия и используется для сравнения различных признаков, выраженных в разных единицах измерения. CV – это относительное выражение среднего квадратического отклонения выражается в %:
. 100%
Оценка генеральных параметров – производится с использованием следующих показателей:
1) критерий достоверности – показатель вероятности безошибочных прогнозов - T. Для определения точности результатов используются формулы ошибок полученных данных:
а) ошибка средней арифметической (m) – показывает репрезентативность этого показателя и вычисляется по формуле:
При увеличении числа измерений стандартная ошибка стремится к нулю.
б) ошибка среднего квадратического отклонения – вычисляется по формуле: 
в) ошибка коэффициента вариации
2) коэффициент достоверности (Т) – используется для установления достоверности различий средних арифметических двух выборок
Т – свидетельствует о наличии статистической достоверности различия между средними арифметическими.
При Т=1,96 - со степенью вероятности 95,0%.
При Т=2,6 – со степенью вероятности 99,0%.
При Т=3,3 – со степенью вероятности 99,9%.
В биологических исследования чаще всего используется критерий надёжности 0,99 или 99,0%, при Т= 2,6
