При всьому різноманітті змісту конкретних робіт з ДО кожне операційне дослідження проходить послідовно наступні основні етапи:
1) постановка задачі - побудова якісної моделі;
2) побудова математичної моделі;
3) знаходження розв’язку;
4) перевірка й коректування моделі;
5) реалізація знайденого розв’язку на практиці.
Охарактеризуємо ці етапи:
1) постановка задачі – це надзвичайно відповідальний етап операційного дослідження.
Спочатку задачу формулюють із погляду замовника. Така постановка звичайно не буває остаточною. Під час аналізу досліджуваної системи задача поступово уточнюється. На цьому етапі роль операційної групи (ОГ) полягає в проведенні ретельного дослідження об'єкта, вивченні множини факторів, що впливають на результати досліджуваного процесу. Після збору дані обстеження і їхнього аналізу ОГ виділяють сукупність істотних факторів, проводить консультації із замовниками та остаточно уточнює змістовну (словесну – якісну) постановку задачі.
2) Побудова математичної моделі – тобто формалізація задачі.
Нагадаємо, що під операцією розуміється керований захід, спрямований на досягнення мети й залежний від деяких параметрів.
Всі фактори, що входять в опис задачі, можна розбити на 2 групи:
– постійні (некеровані) фактори - екзогенні змінні (тобто визначені зовні умови задачі), на які ми впливати не можемо.
Позначимо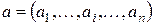 
– вектор заданих параметрів.
– Залежні фактори (ендогенні змінні) - керовані змінні - елементи розв'язку, які ми можемо вибирати за своїм розсудом, тобто керувати ними.
Позначимо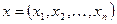 
– вектор керованих параметрів.
У самому загальному випадку математична модель має вигляд:
Знайти такий вектор 
, на якому досягається екстремум функції
(1),
де 
– цільова функція (ЦФ) (показник якості або ефективності).
при обмеженнях 
, 
(2),
де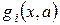 
– функції, що враховують обмеження задачі (наприклад, запаси ресурсів).
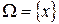– МПР.
Вектор 
, що доставляє екстремум функції , називається оптимальним розв'язком (оптимумом) задачі (або точкою максимуму, або точкою мінімуму) (термінологія пов'язана з геометричною інтерпретацією).
Зауваження 4: Природно задача полягає в знаходженні глобального оптимуму. Таким чином маємо справу із задачею умовної оптимізації (або із задачею на умовний екстремум).
3) знаходження розв'язку.
Зауваження 5. У тих випадках, коли 
й 
хоча б двічі дифференційовані, можна застосовувати класичні методи оптимізації. Однак їхнє застосування є дуже обмеженим, тому що
а) задачі визначення умовного екстремуму дозволяють знайти локальний оптимум, а через багатовимірність функції визначення глобального оптимуму (тобто найбільшого й найменшого значення ЦФ) може виявитися трудомістким або взагалі неможливим (тому що цей оптимум може лежати на границі області розв'язків).
в) класичні методи не працюють, якщо МПР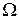 
є дискретною або, якщо функція задана таблично.
У цих випадках для розв'язання задачі (1) – (2) застосовуються методи математичного програмування.
Для знаходження оптимального розв'язку задачі (1) - (2) залежно від вигляду ЦФ і структури обмежень застосовують ті або інші методи знаходження оптимальних розв'язків (методи МП) такі як:
1. Лінійне програмування
якщо функція та обмеження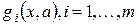 
, – є лінейними щодо змінної 
.
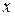2. Нелінійне програмування
якщо та (або) 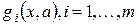, – нелінійні.
Окремі випадки:
2 а) опукле програмування;
2в) квадратичне програмування та ін.
.
3. Дискретне програмування (цілочисельне програмування):
якщо до змінних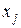 
висувається умова дискретності (наприклад, цілочисельності):
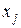– ціле, 
.
4. Динамічне програмування
якщо задача має покрокову структуру (наприклад, є змінна часу) і ЦФ (1) має спеціальну структуру, наприклад, є адитивною або мультиплікативною функцією від змінних 
.
(
– адитивна функція, якщо 
, і
– мультиплікативна, якщо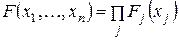 
).
5. Геометричне програмування
якщо ЦФ (1) і обмеження (2) є так званими функціями-позіномами – функції вигляду = 
.
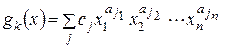6. Параметричне програмування - якщо ЦФ і (або) обмеження залежать від параметрів.
7. Стохастичне програмування - якщо змінні або параметри ЦФ мають випадковий (імовірнісний) характер.
8. Евристичне програмування - застосовують для розв'язання тих задач, у яких точний оптимум знайти алгоритмічним шляхом неможливо через величезне число варіантів.
У такому випадку відмовляються від пошуку оптимального розв'язку й відшукують досить хороший з погляду практики припустимий розв'язок. При цьому користуються спеціальними прийомами - евристиками.
4) перевірка й коректування моделі – перевірка ступеня відповідності або адекватності моделі й реального процесу. Перевірку здійснюють шляхом порівнянням реакції (поведінки) моделі та реального об’єкту при зміні значень некерованих зовнішніх впливів.
5) Реалізація знайденого розв'язку на практиці є найважливішим етапом, що завершує розв'язання задачі.
Впровадження можна розглядати як самостійну задачу, застосувавши до неї й системний підхід, і аналіз.
Отриманий попередньо математичний розв'язок наділяють у відповідну змістовну форму й представляють замовникові у вигляді інструкцій і рекомендацій.
