Синтез оптимального управления организационно-техническими системами
Учебное пособие для выполнения курсовой работы
Москва, 2008 г.
содержание
Введение.. 3
1. Содержание и Методическое Обеспечение курсовой работы 5
1.1 Постановка задачи. 5
Формулировка оптимизационной задачи. 7
1.2. Методика решения задачи синтеза оптимальной позиционной стратегии управления. 8
Численная реализация матрицы обратной связи оптимальной позиционной стратегии управления. 11
2. требования к выполнению курсовой работы... 13
Часть I 15
Часть II 15
3. Варианты Заданий к курсовой работе.. 17
I-я группа заданий (задания: №1, №7, №13) 17
Постановка задачи. 17
Формализация задачи. 18
Формулировка математической задачи. 18
Определение исходных данных: 19
II-я группа заданий (задания: №2, №8, №12, №16) 19
Формализация задачи. 20
Формулировка задачи синтеза оптимального управления. 23
Определение исходных данных: 24
III-я группа заданий (задания: №3, №6, №11, №14) 24
Формализация задачи. 25
Формулировка задачи синтеза оптимального управления. 26
Определение исходных данных: 26
IV-я группа заданий (задания: №4, №5, №9, №10, №15) 28
Формализация задачи. 28
Линеаризация задачи. 29
Формулировка задачи синтеза оптимального управления. 30
Определение исходных данных: 31
4. рекомендации по формированию заключения и Приложений к курсовой работе.. 34
Введение
Учебное пособие предназначено для студентов, выполняющих курсовую работу по дисциплине: «Синтез оптимального управления организационно-техническими системами», читаемой в рамках специальности 0722: «Моделирование и исследование операций в организационно–технических системах».
Целями курсовой работы являются:
- развитие и закрепление навыков постановки задачи на техническом языке (в инженерных терминах по специальности);
- развитие и закрепление навыков математической формализации всех физических составляющих задачи, формулировки её на математическом языке в терминах теории синтеза оптимального управления динамическими системами;
- овладение аналитическими и численными методами синтеза оптимального управления в приложении к задачам оптимизации позиционных стратегий управления организационно-техническими системами (ОТС) по различным критериям и для разных динамических систем;
- приобретение навыков аналитического решения задач синтеза оптимальных позиционных стратегий управления линейными детерминированными динамическими системами на основе применения: достаточных условий оптимальности управления типа Уравнения Беллмана и численных методов интегрирования уравнений Риккати;
- умение разрабатывать методику и конкретизировать алгоритм решения поставленной задачи, формировать и создавать соответствующее программное обеспечение;
- накопление опыта объектно-ориентированного программирования;
- формулирование выводов по результатам проделанной работы.
В пособии имеется подробное описания содержания курсовой работы, сформулированы требования к ней, представлены варианты заданий, приведены теоретические сведения, необходимые для выполнения работы.
Содержание и Методическое Обеспечение курсовой работы
Курсовая работа в значительной мере опирается на аналитическое решение задачи синтеза оптимальной позиционной стратегии управления линейной детерминированной динамической системой (ДС). Это связано с высокой трудоёмкостью решения подобных задач для более сложных ДС в рамках одной курсовой работы. Тем не менее, на примерах решения ряда технических задач (по космической тематике), моделирующихся с помощью линейных детерминированных динамических систем, удается продемонстрировать и отработать минимальный методический набор синтеза оптимальной позиционной стратегии управления.
1.1 Постановка задачи
Рассматривается управляемое движение ЛА, на которое оказывают воздействие различные по своей природе силы и моменты [3, 4, 6, 7, 15, 17]. Величина этих сил и моментов весьма существенно отличается (от нескольких процентов до нескольких порядков). В связи с этим они условно разделены на две группы [11, 14, 15, 16]:
· основные силы и моменты,
· возмущающие силы и моменты.
Предполагается, что под действием первой (основной) группы сил и моментов реализуется основное (номинальное, опорное) движение изучаемого объекта, например, КА; а под действием второй (возмущающей) группы сил осуществляется относительное (по отношению к опорному движению) движение КА, которое часто называют «возмущенным движением».
Имея это в виду, траектория движения объекта может быть представлена как суперпозиция двух движений (см. рис. 1):
· Опорное (номинальное) движение под действием основных (определяющих) сил;
· «Возмущенное» движение под действием возмущающих сил («возмущений»).
Рис. 1
Если считать, что 
- фазовый вектор, характеризующий полное движение объекта, а 
и 
- его опорное (номинальное) и относительное («возмущенное») движение, соответственно. Тогда формально суперпозиция этих двух движений представляется следующим образом.
(1.1)
Если далее предположить, что – мало по отношению к 
, Тогда целесообразно провести линеаризацию 
в окрестности опорной траектории. В результате получим линеаризованные дифференциальные уравнения, моделирующие только возмущенное движение:
(1.2),
В данном случае вектор 
обозначает вектор возмущенного движения – 
, т.е. 
.
где матрицы 
, 
и 
, 
– Якобианы (матрицы частных производных, соответственно, по 
и по 
правых частей нелинейных дифференциальных уравнений 
, полученные в окрестности опорной траектории)
В простейшем случае считается, что эти матрицы состоят из констант (имеют постоянные по времени коэффициенты).
Начало движения ДС (1) определяется точкой (начальным отклонением):
, (1.3)
а заканчивается в фиксированный момент времени:
(1.4)
Формулировка оптимизационной задачи
Определить оптимальную позиционную стратегию управления (закон управления), которая при условии (2) – (3) обеспечит минимум интегро- терминальному (смешенному) критерию:
(1.5).
Как видно из (1.5) критерий имеет квадратичный вид (для таких критериев отсутствуют «изломы» модулей).
Здесь 
и 
– положительно определенные матрицы, задающие с помощью коэффициентов (элементов матриц) значимости управления и состояние системы в конце движения (
задает интегральную значимость управления – 
(для любого момента времени из интервала 
), а 
задает значимость 
).
В итоге фиксация этих коэффициентов определяет оптимальность управления с точки зрения желаемой формы траектории и «затрат» управления на ее реализацию.
1.2. Методика решения задачи синтеза оптимальной позиционной стратегии управления
Для непрерывной детерминированной ДС общего вида и комбинированного функционала (интегротерминального или смешенного):
(1.6)
Достаточное условие оптимальности позиционной стратегии управления в форме уравнения Беллмана принимает вид [8, 9, 11, 14]:
(1.7).
Граничное условиями для него являются:
. (1.8)
В рассматриваемом частном случае для линейной ДС и квадратичного критерия условия (1.7) имеют вид
(1.8)
При конечных условиях:
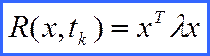(1.9)
Согласно известным необходимым условиям минимума функции по неограниченному аргументу производная этой функции по аргументу в точке минимума должна быть равна нулю. После взятия производной от выражения в фигурных скобках (1.8) и несложных преобразований, получим структуру оптимального управления:
. (1.10)
С учетом (1.10) уравнение Беллмана (1.8) примет вид:
(1.11)
Гипотеза
Предположим, что функция будущих потерь (ФБП) 
для квадратичного критерия (1.5) будет иметь также квадратичный вид:
, (1.12)
где матрица 
в общем случае является функцией времени
(1.13)
и имеет размерность 
.
С учетом предположения (1.12) уравнение (1.11) примет вид:
(1.14).
Отсюда следует, что матрица 
должна удовлетворять матричному дифференциальному уравнению Риккати [8, 9, 11, 14]:
(1.15).
При этом согласно (1.9) оно дополняется конечными условиями:
(1.16)
Таким образом, с учетом предположения для ФБП (1.12) закон управления (позиционная стратегия) примет следующий вид:
, (1.17)
где 
– матрица обратной связи для оптимального закона (позиционной стратегии) управления:
. (1.18)
Из полученных выражений видно, что ключевым звеном в процедуре синтеза является определение матрицы 
.
Численная реализация матрицы обратной связи оптимальной позиционной стратегии управления
Согласно (1.16) матрица 
определяется терминальной частью квадратичного критерия – матрицей l в момент времени tk:
При этом каждая составляющая вектора l задаёт значимость («вес») соответствующей составляющей вектора состояния системы в момент tk. Поскольку поставлена задача минимизации критерия (1.6), то чем больше «вес» составляющей вектора состояния в конце движения, тем относительно более низкого её значения требует решаемая задача.
Зависимость матрицы от времени предлагается установить путем численного интегрирования (например, методом Рунге-Кутта 4-го порядка) матричного уравнения Риккати (1.15) в «обратном» времени.
Конечной целью курсовой работы является определение такого сочетания составляющих вектора l, которое по мнению исполнителя работы будет удовлетворительным с точки зрения математической и технической постановки задачи. Другими словами, необходимо провести исследование влияния значений составляющих вектора коэффициентов l, которые в данном случае становятся варьируемыми параметрами, на величину конечных отклонений составляющих вектора 
, имеющих вполне конкретный технический смысл.
Результаты исследования должны сопровождаться графиками зависимостей 
от параметров l1, l2,…, ln и соответствующими техническими комментариями.
Замечание
Для ускорения и автоматизации процесса построения указанных зависимостей рекомендуется применить процедуры планируемого перебора и методы параметрической оптимизации (математического программирования).
требования к выполнению курсовой работы
Каждый студент получает индивидуальный вариант задания, в который включаются:
1. Описание физической и технической задачи курсовой работы.
2. Обобщенная математическая формализация задачи.
3. Формулировка оптимизационной задачи синтеза позиционной стратегии управления.
4. План проведения индивидуальных параметрических исследований в рамках конкретного задания для каждого варианта курсовой работы.
Процесс проведения курсовой работы строго регламентирован и должен выполняться согласно плану, представленному в табл 1.1.
Таблица 1.1
| № п/п | Содержание | продолжитель-ность | основная литература |
| Изучение и постановка конкретной задачи согласно выданному варианта курсовой работы, оформление соответствующего раздела в отчет по КР | 1 неделя | конспект лекций | |
| изучение методики решения задачи, оформление соответствующего раздела в отчет по КР | 0,5 недели | [1, 2], конспект лекций | |
| решение задачи в черновом виде | 1,5 недели | конспект семинарских занятий |
Продолжение Таблицы 1.1
| проведение исследований по коэффициентам значимости в критерии оптимальности, построение графиков зависимости фазового состояния ДС и управления от времени | 1 неделя | конспект семинарских занятий | |
| оформление части I отчета по КР | 0,5 недели | ||
| изучение теории и разработка методик численного решения задачи (согласно заданию), оформление раздела в отчет по КР | 0,5 недели | [1, 2, 3, 7, 8, 9], конспект лекций и семинарских занятий | |
| формирование алгоритмов (блок-схем), программирование и отладка программного обеспечения | 2 недели | [1, 2, 7, 8, 9], конспект лекций и семинарских занятий | |
| построение графиков зависимости фазового состояния ДС и управления от времени для численного решения задачи и проведение сравнения с аналитическим решением | 0,5 недели | ||
| оформление части II отчета по КР | 0,5 недели | ||
| Анализ результатов и формулировка выводов по КР | 0,5 недели |
Как видно из плана проведения КР ее реализация рассчитана на ~ 8,5 недель, что составляет по продолжительности около 53 % семестра.
Отчет по КР должен быть оформлен согласно действующему ГОСТу на оформление научно-технических отчетов и удовлетворять следующим требованиям.
· Отчет по КР должен иметь титульный лист, на котором должны быть указаны: дисциплина, в рамках которой выполняется КР, учебное заведение, факультет и кафедра, где выполнялась КР, автор и руководители КР, а также год выполнения КР;
· Вслед за титульным листом Отчет по КР должен иметь лист - «Задание на КР», на котором компактно излагаются индивидуальные технические задачи; задаются соответствующие динамические системы, моделирующие движение КА, а также критерии оптимальности управления этими системами. (Задаются преподавателем, контролирующим выполнение КР);
· Затем за листом «Задание на КР» должно следовать Содержание отчета по КР;
Часть I
Отчет по КР должен иметь:
· раздел, посвященный общей и частной постановке задачи с привлечением принятой в данной дисциплине терминологии и математических обозначений;
· должен иметь раздел, посвященный методике и алгоритму аналитического решения поставленной задачи (формализм применения достаточных условий оптимальности управления типа уравнения Беллмана);
· должен иметь раздел, в котором описано (детально) конкретное решение поставленной задачи, оформленное согласно общему алгоритму решения подобных задач.
Часть II
Отчет по КР должен иметь:
· раздел, посвященный описанию методик и алгоритма (блок-схемы) исследования влияния коэффициентов значимости матрицы λ в критерии (1.6) на величину конечных отклонений составляющих вектора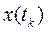 
, имеющих конкретный технический смысл;
· раздел, посвященный описанию результатов численных исследований в виде соответствующих таблиц и графиков, графических изображений управлений и соответствующих траекторий движения для рекомендуемых сочетаний коэффициентов значимости матрицы λ (все полученные результаты должны сопровождаться содержательными комментариями по существу решаемой технической задачи).
· В заключении КР должны быть сформулированы выводы по проделанной исследовательской работе, в которых должны даваться рекомендации по синтезированному оптимальному управлению для соответствующего конкретного критерия (1.6).
· В Приложении к КР должны быть помещены: распечатки модулей программного обеспечения, соответствующие блок-схемам численных алгоритмов решения и анализа задачи оптимизации программного управления заданной динамической системой.
Варианты Заданий к курсовой работе
Варианты заданий к курсовой работе разделены по четырём техническим направлениям, в которых применяется тория синтеза оптимальных позиционных стратегий управления. В свою очередь, каждое направление включает в себя несколько вариантов индивидуальных заданий, имеющих собственные особенности и требующие проведения оригинальных исследований.
I-я группа заданий (задания: №1, №7, №13)
В первой группе заданий рассматриваются задачи управления угловым движением ЛА, предполагающего наличие точной информации о положении связанной системы координат ЛА относительно заданной инерциальной системы отсчета (например, относительно земной топоцентрической системы координат). Для упрощения задачи (носящего непринципиальный характер, с точки зрения выполняемой КР) моделирование движения ЛА осуществляется только в продольном канале (относительно связанной оси 0Z).
Постановка задачи
Угловое движение ЛА относительно связанной оси 0Z с достаточной точностью описывается системой дифференциальных уравнений вида:
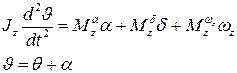(3.1)
где: 
- угол тангажа; 
- угол наклона траектории; 
- угол атаки; 
- угол отклонения руля высоты; 
- угловая скорость вращения вокруг оси 0Z; 
- момент инерции; 
, 
, 
- частные производные момента относительно оси 0Z по соответствующим переменным.
В начале движения ЛА имеет некоторое нежелательное отклонение от номинального угла тангажа, которое необходимо минимизировать до приемлемого значения за некоторое допустимое время – T (время окончания переориентации). Кроме того, угловая скорость вокруг оси 0Z должна быть максимально приближена к нулю:
, 
В качестве управления рассматривается угол отклонения руля высоты ЛА, на который накладывается ограничение:
Формализация задачи
Предполагая, что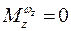 
(нет демпфирования) и 
(опорная траектория не меняется), а оптимальное управление u = 
не нарушает указанного ограничения, исходная система (3.1) преобразуется к виду:
(3.2)
Если далее ввести обозначение угла атаки и его скорости изменения через вектор 
, тогда уравнение (3.2) можно их свести к двум уравнениям, записанным в форме Коши:
(3.3)
где 
; 
Формулировка математической задачи
Определить (синтезировать) оптимальную позиционную стратегию управления u(x) системой (3), минимизирующую квадратичный критерий оптимальности:
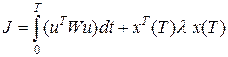(3.4)
Где W, l - матрицы весовых коэффициентов (коэффициентов значимости), подлежащих определению, наряду со временем окончания переориентации - Т
Определение исходных данных:
Вариант №1
(3.5)
Вариант №7
(3.6)
Вариант №13
(3.7)
Вариант №17
(3.7’)
II-я группа заданий
(задания: №2, №8, №12, №16)
Во второй группе заданий рассматриваются задачи управления движением центра масс стационарного ИСЗ (СИСЗ) посредством малой тяги корректирующей двигательной установки (КДУ). Целью управления является перевод СИСЗ вдоль круговой орбиты (r 0= 42164888, V 0 =3074,7 м/с, Т 0 = 86164с, ω0 = 0.72921 рад/с) из одной точки «висения» в другую при минимальных затратах топлива.
Формализация задачи
Уравнения движения, моделирующие движение СИСЗ, заданы в полярной системе координат:
(3.8)
где 
- радиус-вектор, 
- угловая полярная координата,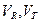 
- радиальная и трансверсальная составляющие скорости, 
- гравитационная составляющая Земли, 
- управляющие ускорения, создаваемые корректирующей ДУ, в радиальном и трансверсальном направлениях, соответственно.
Перейдем в уравнениях (1) к безразмерным величинам:
(3.9)
где безразмерные переменные отмечены символом (*), r0 – радиус стационарной орбиты СИСЗ, u* - относительное ускорение, измеряемое в долях ускорения свободного падения на высоте стационарной орбиты СИСЗ.
С учетом введения безразмерных величин (3.9) и опуская символ (*), получим:
(3.10)
Полагая, что в процессе перевода СИСЗ из одной точки «висения» в другую, отклонения 
, 
, 
, 
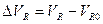фазовых координат 
от соответствующих значений 
на круговой стационарной орбите радиуса r 0 достаточно малы, линеаризуем уравнения (3.10) в окрестности круговой орбиты единичного радиуса (в безразмерных координатах) и получим модель движения в отклонениях:
(3.11)
В матричном виде уравнения (3.11) будут следующими.
, (3.12)
Где
(3.13)
Начальное состояние СИСЗ, заданное в отклонениях, по условию задачи – нулевой вектор, за исключением углового «расстояния» по орбите 
, на которое необходимо перевести СИСЗ, т.е.
. (3.14)
Терминальное (конечное) состояние СИСЗ, заданное в отклонениях, определяется нулевым вектором:
, (3.15)
где 
- время завершения процесса перевода (подлежит определению).
В качестве вектора управления рассматривается управляющие ускорения СИСЗ, создаваемые КДУ. Считается, что величина тяги двигателей КДУ ограничена:
или 
(3.16)
где um – максимальное относительное ускорение, создаваемое двигателем, измеряемое в долях ускорения свободного падения (определяет расход рабочего тела).
Если предположить, что ограничение на управление и фиксация терминальных условий могут быть с небольшими погрешностями заменены косвенными ограничениями вида:
(3.17)
где 
- матрица коэффициентов значимости составляющих вектора фазового состояния в конечный момент времени;
- матрица коэффициентов значимости составляющих вектора управления в процессе движения системы.
С учетом проведенной математической формализации задачи можно поставить оптимизационную задачу.
Формулировка задачи синтеза оптимального управления
Определить (синтезировать) оптимальную позиционную стратегию управления u(x) системой (3.12), обеспечивающую с учетом (3.17) минимум квадратичного критерия оптимальности:
(3.18)
Где W, l - матрицы весовых коэффициентов (коэффициентов значимости), подлежащих определению, наряду со временем окончания процесса перевода - Т
Задания
1. Сформировать структуру оптимальной позиционной стратегии управления u(x) (зависящую от матрицы 
), используя достаточные условия в форме уравнения Беллмана.
2. Численно проинтегрировать матричные дифференциальные уравнения типа Риккати с целью получения (запомнить в дискретном виде) зависимости матрицы от времени.
3. Численно проинтегрировать уравнения движения СИСЗ (3.12), управляемого согласно оптимальной позиционной стратегии u(x).
4. Провести исследование всех составляющих вектора x(t) и оптимальной стратегии u(x) по времени tÎ[t0, T] для варьируемых значений весовых коэффициентов матриц l и W с целями:
· удовлетворения ограничений (3.17) с наибольшим запасом (что будет означать максимальную экономию топлива);
· выбора наиболее приемлемых решений по фазовому и конечному состоянию СИСЗ (отклонения от требуемого фазового состояния).
5. Построить графики зависимости: u(x), u(t), x(t); tÎ[t0, T], x1(x2) для рекомендуемых коэффициентов матриц l и W.
Определение исходных данных:
Вариант №2
Требуемый угол перевода СИСЗ по стационарной орбите от φ = 60 угл. градусов до 0 угл. градусов;
Вариант №8
Требуемый угол перевода СИСЗ по стационарной орбите от φ = 40 угл. градусов до 0 угл. градусов;
Вариант №12
Требуемый угол перевода СИСЗ по стационарной орбите от φ = 30 угл. градусов до 0 угл. градусов;
Вариант №16
Требуемый угол перевода СИСЗ по стационарной орбите от φ = 20 угл. градусов до 0 угл. градусов;
III-я группа заданий
(задания: №3, №6, №11, №14)
В третьей группе заданий рассматриваются задачи перевода КА на требуемую круговую орбиту с некоторой заданной в окрестности этой орбиты траектории. КА имеет двигательную установку, способную создавать управляющее ускорение u центра масс КА вдоль трансверсали к траектории. Необходимо определить оптимальную позиционную стратегию управления движением центра масс КА, обеспечивающую минимальные энергетические затраты в ходе операции перевода КА.
Формализация задачи
Предполагая, что на центр масс КА действуют только гравитационная сила и сила тяги, уравнения движения в полярной плоской системе координат будут иметь следующий вид.
(3.19)
где: r и θ - полярные координаты траектории; kЗ – гравитационная постоянная Земли.
Терминальные (конечные) условия выведения определяются параметрами требуемой орбиты:
где ω0 – угловая скорость обращения по орбите назначения, T0 – период обращения.
Предполагая, что отклонения начального положения центра масс КА от требуемой круговой орбиты: 
- малы, линеаризуем уравнения (3.19) относительно параметров этой орбиты. В результате получим следующие уравнения относительного движения.
(3.20)
Если при этом ввести новые обозначения:
,
тогда уравнения (3.20) могут быть представлены в виде:
(3.21)
Начальное состояние задано вектором x0, конечное состояние в силу относительности движения определяется как нулевой вектор: x(tk) = 0, где tk – время окончания операции перевода КА.
Формулировка задачи синтеза оптимального управления
Определить (синтезировать) оптимальную позиционную стратегию управления u(x) системой (3.21), минимизирующую квадратичный критерий оптимальности:
(3.22)
Где W, l - матрицы весовых коэффициентов (коэффициентов значимости), подлежащих определению, наряду со временем окончания операции перевода - tk.
Задание
1) Сформировать структуру оптимальной позиционной стратегии управления u(x), зависящую от матрицы , которая должна удовлетворять системе дифференциальных уравнений типа Риккати.
2) Проинтегрировать (в «обратном» времени) уравнения типа Риккати с целью получения оптимальной позиционной стратегии управления u(x).
3) Для варьируемых значений элементов матриц W, l и времени tk провести исследование поведения стратегии u(x) и соответствующих составляющих вектора x(t), tÎ[t0, tk].
4) Построить графики зависимости: u(x), u(t), x(t); tÎ[t0, tk], x1(x2).
Определение исходных данных:
Вариант №3
- гравитационная постоянная Земли - k З = 3.986∙1014 [м3/с2]
- период обращения - T0 = 1 сутки
- вектор состояния в момент начала управляемого движения:
Вариант №6
- гравитационная постоянная Земли - k З = 3.986∙1014 [м3/с2]
- период обращения - T0 = 0,2 суток
- вектор состояния в момент начала управляемого движения:
Вариант №11
- гравитационная постоянная Земли - k З = 3.986∙1014 [м3/с2]
- период обращения - T0 = 0,5 суток
- вектор состояния в момент начала управляемого движения:
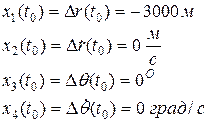
Вариант №14
- гравитационная постоянная Земли - k З = 3.986∙1014 [м3/с2]
- период обращения - T0 = 1 сутки
- вектор состояния в момент начала управляемого движения:
IV-я группа заданий
(задания: №4, №5, №9, №10, №15)
В четвёртой группе заданий рассматриваются задачи спуска специального посадочного аппарата – пенетратора в заданную область поверхности Марса с максимальной точностью. Пенетратор имеет двигательную установку, позволяющую создавать ограниченное управляющие ускорение a< amax перпендикулярно траектории спуска (в вертикальной плоскости). Необходимо определить оптимальную позиционную стратегию управления, обеспечивающую минимальные энергетические затраты при спуске пенетратора.
Формализация задачи
Предполагая, что на пенетратор действуют только гравитационная и управляющая силы, а также считая, что спуск пенетратора осуществляется по траектории с большими углами наклона траектории и с небольшой высоты, то есть высота полета является монотонной функцией времени (только убывает), уравнения движения пенетратора в скоростной плоской системе координат будут иметь следующий вид (высота h рассматривается в качестве независимой переменной).
(3.23)
где: v, θ, h, l – соответственно скорость, угол наклона траектории, высота и дальность спуска пенетратора; g0 – ускорение свободного падения на Марсе - 3.73∙[м/с2].
Начальные условия спуска определяются для каждого варианта задания индивидуально. Высота окончания спуска - момент касания поверхности Марса: hk=0 – фиксирует терминальное (конечное) состояние системы (3.23).
Линеаризация задачи
Пусть определена опорная траектория с указанными выше начальными условиями: v0, θ0 и l0 = 0 м, которая обеспечивает требуемое попадание пенетратора в заданную точку на поверхности Марса. Предполагая, что отклонения 
, вызываемые действующими возмущениями, малы, линеаризуем уравнения (3.23) относительно опорной траектории xопор (∙).
Если ввести новые обозначения 
, а также рассматривать управление только как корректирующее полет пенетратора, то есть a = aопор +u, при aопор = 0, то линеаризованные уравнения возмущенного движения в вариациях можно представить в виде:
(3.24)
где А(h) и В(h) – матрицы частных производных по вектору фазового состояния и управлению системы (3.23) соответственно. Очевидно, что их коэффициенты будут зависеть от высоты h:
,
Моментом окончания спуска следует считать hk = 0.
Формулировка задачи синтеза оптимального управления
Определить (синтезировать) оптимальную позиционную стратегию управления u(x) системой (3.24), минимизирующую квадратичный критерий оптимальности:
(3.25)
Где W, l - матрицы весовых коэффициентов (коэффициентов значимости).
Задание
1) Проинтегрировать уравнения движения (3.23) и «запомнить» зависимости v(h), θ(h) (для заданных граничных условий) с целью вычисления переменных коэффициентов матриц А(h) и В(h).
2) Сформировать структуру оптимальной позиционной стратегии управления u(x), зависящую от матрицы , которая должна удовлетворять системе дифференциальных уравнений типа Риккати.
3) Проинтегрировать с учетом А(h) и В(h) уравнения типа Риккати с целью получения оптимальной позиционной стратегии управления u(x).
4) Для варьируемых значений матриц (весовых коэффициентов) W и l провести исследование поведения стратегии u(x) и соответствующих составляющих вектора x(h), hÎ[h0, hk]
5) Построить графики зависимостей: u(x), u(h), x(h); hÎ[h0, hk], x1(x2).
Определение исходных данных:
Вариант №4
Для данного варианта определены следующие начальные условия:
· скорость входа КА в атмосферу Марса – v0 = 2000 м/с;
· угол наклона траектории – θ0 = - 20 град.
Высота включения системы наведения пенетратора в заданную точку на поверхности Марса – h0 = 6000 м.
В качестве возмущений предлагается рассматривать отклонения от заданных начальных условий: l0 θ0 на высоте – h0, а именно:
Вариант №5
Для данного варианта определены следующие начальные условия:
· скорость входа КА в атмосферу Марса – v0 = 3000 м/с;
· угол наклона траектории – θ0 = - 15 угл.град.
Высота включения системы наведения пенетратора в заданную точку на поверхности Марса – h0 = 5000 м.
В качестве возмущений предлагается рассматривать отклонения от заданных начальных условий: l0 θ0 на высоте – h0, а именно:
Вариант №9
Для данного варианта определены следующие начальные условия:
· скорость входа КА в атмосферу Марса – v0 = 2500 м/с;
· угол наклона траектории – θ0 = - 10 угл.град.
Высота включения системы наведения пенетратора в заданную точку на поверхности Марса – h0 = 7000 м.
В качестве возмущений предлагается рассматривать отклонения от заданных начальных условий: l0 θ0 на высоте – h0, а именно:
Вариант №10
Для данного варианта определены следующие начальные условия:
· скорость входа КА в атмосферу Марса – v0 = 3500 м/с;
· угол наклона траектории – θ0 = - 5 угл.град.
Высота включения системы наведения пенетратора в заданную точку на поверхности Марса – h0 = 8000 м.
В качестве возмущений предлагается рассматривать отклонения от заданных начальных условий: l0 θ0 на высоте – h0, а именно:
Вариант №15
Для данного варианта определены следующие начальные условия:
· скорость входа КА в атмосферу Марса – v0 = 4000 м/с;
· угол наклона траектории – θ0 = - 7 угл.град.
Высота включения системы наведения пенетратора в заданную точку на поверхности Марса – h0 = 9000 м.
В качестве возмущений предлагается рассматривать отклонения от заданных начальных условий: l0 θ0 на высоте – h0, а именно:
