Пример 1. 
Пр.2 
Пр. 3 
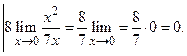
Пример 2. 
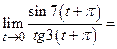
Пример 3. 
Пр. 2 
Пример 4. 
Пример5. 
Пр.4,Пр.6 
Пр.6 
Пример 6. 
(Пр.5)=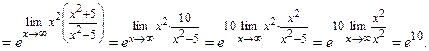 
Пример 7. 
Пример 8.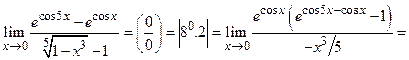 
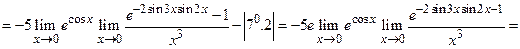
Пример 9. 
не определен из-за знака 
1) 
2) 
Пр.4 
Таким образом, существуют различные односторонние 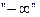на 
и на 
пределы.
Указания к заданию 5.
Пример. Докажите, что
и 
бесконечно малые функции одного порядка при 
Найдите значение постоянной “C”, при котором они будут эквивалентны.
Решение.
Пр. 
Пр. 
Пр.3 
при 
Пример выполнения задания 5.
Определите порядок относительно “ x ” функции
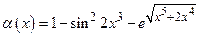
бесконечно малой при
Решение.
при 
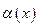- бесконечно малая одного порядка по отношению к 
, то сеть второго порядка относительно “ x ”.
Указания к выполнению задания 7.
При исследовании функции на непрерывность пользуются теоремой о непрерывности элементарных функций там, где они определены; признаком непрерывности фуки в точке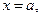 
когда
(2.19)
При наличии точек разрывов исследуют функции в их окрестности и соответствующим образом классифицируют.
Пример 1. Исследовать функцию на непрерывность и построить её схематический график, если
Решение. Сначала найдем область определения функции
Область определения симметрична относительно начала координат, следует исследовать функцию на признак четности.
функция нечетная и её график симметричен относительно начала координат. Таким образом, достаточно исследовать функцию на промежутке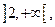 
построить график, а затем отобразить его симметрию начала координат.
1) В точке 
функция определена справа, поэтому найдем лишь правосторонний предел в ней:
- точка бесконечного разрыва (П-рода), не входит в 
2) На получим
график приближается к оси OX (= 0) снизу при 
3) Для уточнения графика найдем дополнительную точку 
Заданная функция элементарная, и область её непрерывности совпадает с областью определения
- область непрерывности.
Строим график для 
а затем достраиваем для 
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
2.1. Найти и изобразить на числовой оси области определения функций:
ВАРИАНТ 1.
1) 
2) 
3) 
ВАРИАНТ 2.
1) 
2) 
3) 
ВАРИАНТ 3.
1) 
2) 
3) 
ВАРИАНТ 4.
1) 
2) 
3) 
ВАРИАНТ 5.
1) 
2) 
3) 
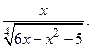
ВАРИАНТ 6.
1) 
2) 
3) 
ВАРИАНТ 7.
1) 
2) 
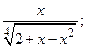3) 
ВАРИАНТ 8.
1) 
2) 
3) 
ВАРИАНТ 9.
1) 
2) 
3) 
ВАРИАНТ 10.
1) 
2) 
3) 
ВАРИАНТ 11.
1) 
2) 
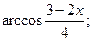3) 
ВАРИАНТ 12.
1) 
2) 
3) 
ВАРИАНТ 13.
1) 
2) 
3) 
ВАРИАНТ 14.
1) 
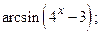
2) 
3) 
ВАРИАНТ 15.
1) 
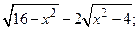
2) 
3) 
ВАРИАНТ 16.
1) 
2) 
3) 
ВАРИАНТ 17.
1) 
2) 
3) 
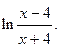
ВАРИАНТ 18.
1) 
2) 
3) 
ВАРИАНТ 19.
1) 
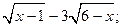
2) 
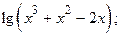3) 
ВАРИАНТ 20.
1) 
2) 
3) 
ВАРИАНТ 21.
1) 
2) 
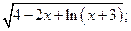3) 
ВАРИАНТ 22.
1) 
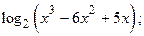
2) 
3) 
ВАРИАНТ 23.
1) 
2) 
3) 
ВАРИАНТ 24.
1) 
2) 
3) 
ВАРИАНТ 25.
1) 
2) 
3) 
ВАРИАНТ 26.
1) 
2) 
3) 
ВАРИАНТ 27.
1) 
2) 
3) 
ВАРИАНТ 28.
1) 
2) 
3) 
ВАРИАНТ 29.
1) 
2) 
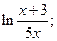3) 
ВАРИАНТ 30.
1) 
2) 
3) 
2.2. Исследовать заданные функции на четность и нечетность, найти интервалы законопостоянства:
ВАРИАНТ 1. 1) 
2) 
ВАРИАНТ 2. 1) 
2) 
ВАРИАНТ 3. 1)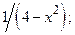 
2) 
ВАРИАНТ 4. 1)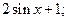 
2) 
ВАРИАНТ 5. 1) 
2) 
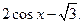
ВАРИАНТ 6. 1) 
2) 
ВАРИАНТ 7. 1) 
2) 
ВАРИАНТ 8. 1) 
2) 
ВАРИАНТ 9. 1) 
2) 
ВАРИАНТ 10. 1) 
2) 
ВАРИАНТ 11. 1) 
2) 
ВАРИАНТ 12. 1) 
2) 
ВАРИАНТ 13. 1) 2) 
ВАРИАНТ 14. 1) 
2) 
ВАРИАНТ 15. 1) 
2) 
ВАРИАНТ 16. 1) 
2)
ВАРИАНТ 17. 1) 
2) 
ВАРИАНТ 18. 1) 
2) 
ВАРИАНТ 19. 1) 
2) 
ВАРИАНТ 20. 1) 
2) 
ВАРИАНТ 21. 1) 
2) 
ВАРИАНТ 22. 1) 
2) 
ВАРИАНТ 23. 1)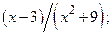 
2) 
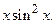
ВАРИАНТ 24. 1) 
2) 
ВАРИАНТ 25. 1) 
2) 
ВАРИАНТ 26. 1)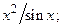 
2) 
ВАРИАНТ 27. 1) 
2) 
ВАРИАНТ 28. 1) 
2) 
ВАРИАНТ 29. 1)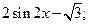 
2) 
ВАРИАНТ 30, 1) 
2) 
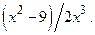
2.3. Построить замкнутые области, ограниченные заданными линиями и удовлетворяющие приведенным ограничениям:
ВАРИАНТ 1. 1) 
2) 
3) 
ВАРИАНТ 2. 1)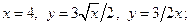 
2) 
3) 
ВАРИАНТ 3, 1) 
2) 
3) 
ВАРИАНТ 4. 1) 
2) 
3) 
ВАРИАНТ 5. 1) 
2) 
3) 
ВАРИАНТ 6. 1) 
2) 
3) 
ВАРИАНТ 7. 1) 
2) 
3) 
ВАРИАНТ 8. 1)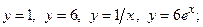 
2) 
3) 
ВАРИАНТ 9. 1) 
2) 
3) 
ВАРИАНТ 10. 1) 
2) 
3) 
ВАРИАНТ 11. 1) 
2) 
3) 
ВАРИАНТ 12. 
ВАРИАНТ 13. 
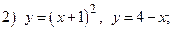
ВАРИАНТ 14. 
ВАРИАНТ 15. 
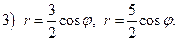
ВАРИАНТ 16. 
ВАРИАНТ 17. 
ВАРИАНТ 18. 
ВАРИАНТ 19. 
ВАРИАНТ 20. 
ВАРИАНТ 21. 
ВАРИАНТ 22. 
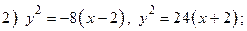
ВАРИАНТ 23. 
ВАРИАНТ 24.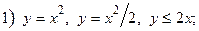 
ВАРИАНТ 25. 
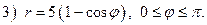
ВАРИАНТ 26. 
ВАРИАНТ 27. 
ВАРИАНТ28. 
ВАРИАНТ 29. 
ВАРИАНТ 30. 
2.4. Найти указанные пределы:
ВАРИАНТ 1.
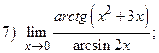
ВАРИАНТ 2.
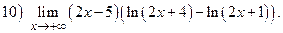
ВАРИАНТ 3.
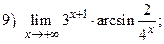
ВАРИАНТ 4.
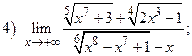
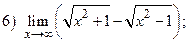
ВАРИАНТ 5.
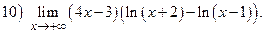
ВАРИАНТ 6.
ВАРИАНТ 7.
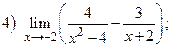
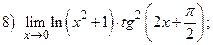
ВАРИАНТ 8.
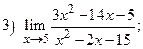
ВАРИАНТ 9.
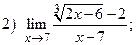
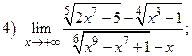
ВАРИАНТ 10.
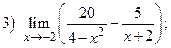
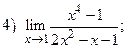
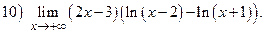
ВАРИАНТ 11.
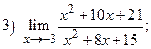
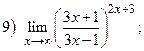
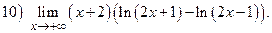
ВАРИАНТ 12.
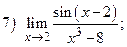
ВАРИАНТ 13.
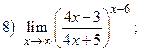
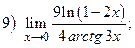
ВАРИАНТ 14.
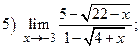
ВАРИАНТ 15.
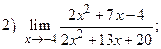
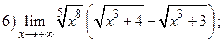
ВАРИАНТ 16.
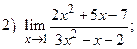
ВАРИАНТ 17.
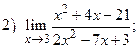
ВАРИАНТ 18.
ВАРИАНТ 19.
ВАРИАНТ 20.
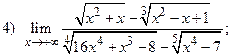
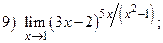
ВАРИАНТ 21.
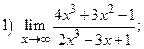
ВАРИАНТ 22.
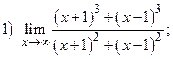
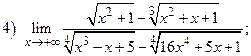
ВАРИАНТ 23.
ВАРИАНТ 24.
ВАРИАНТ 25.
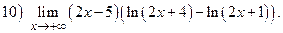
ВАРИАНТ 26.
ВАРИАНТ 27.
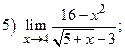
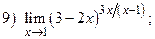
ВАРИАНТ 28.
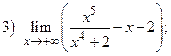
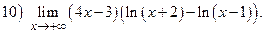
ВАРИАНТ 29.
ВАРИАНТ 30.
