Пример выполнения курсового проекта

Состав и объем курсового проекта

Курсовой проект состоит из расчетно-пояснительной записки (РПЗ) с иллюстративным графическим материалом, размещенным по разделам проекта, чертежей и схем.

РПЗ объемом от 20-25 страниц содержит:

титульный лист; задание на курсовой проект; содержание; введение – 1-2 c; основную часть (теоретическую, практическую, расчетную, исследовательскую) – 20-30 с; заключение 1-2 с; приложение (при необходимости); список использованных источников.

Во введении должна быть дана оценка современного состояния уровня развития “Микросхемотехники” и ее роль в разработке новых ИС и БИС по субмикронной КМОП-технологии, актуальность, цели и задачи, решаемые в курсовом проекте.

Основная часть курсового проекта должна содержать подробное обоснование реализации теоретической, практической и расчетной частей в последовательности:

1) по заданному алгоритму – логическому булевому уравнению (приложение 1), описывающему работу проектируемого устройства, построить автомат в общем виде, используя основные логические элементы без привязки к конкретной серии ИС;

2) используя аксиомы, теоремы, законы и правила алгебры логики Буля, произвести минимизацию исходного логического уравнения;

3) для заданного логического уравнения построить таблицу истинности и карту Карно;

4) построить комбинационное устройство по полученной минимальной форме уравнения на основе базовых логических элементов;

5) минимальную форму логического уравнения представить в базисах И-НЕ и ИЛИ-НЕ и на их основе построить соответствующие устройства;

6) дать предварительную сравнительную оценку технико-экономических показателей минимизированных устройств, сопоставляя с “лобовым” вариантом;

7) нарисовать электрические схемы, построенные по “лобовому решению” и в базисах И-НЕ и ИЛИ-НЕ с использованием ГОСТ 2.701-84 “ЕСКД. Схемы. Виды и типы. Общие требования к выполнению” и ГОСТ 2.709-81 “ЕСКД. Правила выполнения электрических схем цифровой вычислительной техники”;

8) используя схемный редактор САПР ПЛИС Quartus II компании Altera нарисовать “лобовое решение” по заданному логическому уравнению и в базисах И-НЕ и ИЛИ-НЕ;

9) в автоматическом режиме, используя САПР ПЛИС Quartuse II синтезировать булевы логические уравнения и сравнить их с уравнениями полученными с использованием аксиом, теорем, законов и правил алгебры логики Буля.

10) осуществить функциональное моделирование электрической схемы построенной по “лобовому” решению, сравнить результаты моделирования с таблицей истинности и представить временные диаграммы.

11) обосновать оптимальный вариант схемотехнического решения на базе ИС 74НС серии с использованием технико-экономических показателей (мощность потребления, быстродействие, надежность)

Пример выполнения курсового проекта

По заданному алгоритму – булевому логическому уравнению – построить вариант комбинационного устройства в общем виде:

. (1)

Пользуясь правилами алгебры логики, проведем минимизацию исходного логического уравнения:

= =

= = (2)

= = (3)

= = (4)

= . (5)

Далее, по заданному логическому уравнению (1) построим таблицу истинности (табл.1). По последнему правому столбцу таблицы построим каноническую сумму минтермов или стандартную сумму произведений:

. (6)

Сравнивая логические уравнения (2) и (6) видим, что они идентичны.

По таблице истинности построим карту Карно для функции четырех переменных.

AB	CD

По заданному логическому уравнению (1) и его минимизированным решениям (4) и (5) нарисуем электрические схемы с использованием схемного редактора САПР ПЛИС Quartus II (рис.1). На рис.1 обозначено выход комбинационной схемы по уравнению (1); выход схемы по уравнению (4); выход схемы по уравнению (5). Для размещения проектируемой комбинационной схемы выберем ПЛИС по архитектуре ППВМ (программируемые пользователем вентильные матрицы, в зарубежной аббревиатуре FPGA) APEX20K.

В момент компиляции комбинационной схемы построенной по уравнению (1) (логический синтез) САПР ПЛИС Quartus II будет применен ряд патентованных алгоритмов, направленные на минимизацию использования ресурсов. После логического синтеза схемы в САПР ПЛИС Quartus II имеем:

= =

= .

Файл отчета в САПР ПЛИС Quartus II, после логического синтеза (булева функция реализуется на таблицах перекодировок LUT, меню Option & Parameter Settings, установка технология маппирования Technology Mapper LUT) имеет вид:

A1L6 = A & D & (B $!C) #!A &!D & (B $!C);

A = INPUT();

D = INPUT();

B = INPUT();

C = INPUT();

F = OUTPUT(A1L6);

QQQQ = OUTPUT(A1L6);

MMMM = OUTPUT(A1L6);

Выберем другую технологию маппирования для ПЛИС APEX– термы произведений (установка Product Term) и осуществим логический синтез. Файл отчета в САПР ПЛИС Quartus II, после логического синтеза имеет вид:

A1P21_p1_out = A & D &!B &!C;

A1P21_p2_out = A & D & B & C;

A1P21 = A1P21_p1_out # A1P21_p2_out # A1P31;

A1P01_p1_out = A & D &!B &!C;

A1P01_p2_out = A & D & B & C;

A1P01 = A1P01_p1_out # A1P01_p2_out # A1P11;

A1P31_p2_out =!A &!D & B & C;

A1P31_p1_out =!A &!D &!B &!C;

A1P31 = A1P31_p2_out # A1P31_p1_out;

A1P11_p2_out =!A &!D & B & C;

A1P11_p1_out =!A &!D &!B &!C;

A1P11 = A1P11_p2_out # A1P11_p1_out;

A = INPUT();

D = INPUT();

B = INPUT();

C = INPUT();

F = OUTPUT(A1P21);

QQQQ = OUTPUT(A1P01);

MMMM = OUTPUT(A1P01);

Представим полученную информацию в привычном для нас виде:

Таким образом, на этапе автоматической компиляции САПР Quartuse выдал нам минимизированное уравнение (2).

Из отчета видим, что схемы представленные на рис.1, построены по уравнениям (1), (4) и (5) тождественны. Но реализация логических функций на базе LUT таблиц более эффективно.

Применив закон двойного отрицания, реализуем устройство в двух основных базисах (И-НЕ, ИЛИ-НЕ), что позволяет на практике получить существенный выигрыш в технико-экономических показателях. В начале реализуем устройство в базисе И-НЕ. Целесообразно воспользоваться уравнением (3):

. (7)

Комбинационная схема по логическому уравнению (7) в базисе И-НЕ показана на рис.2, а. Продолжим дальнейшее применение теорем булевой алгебры и построим комбинационную схему в базисе ИЛИ-НЕ:

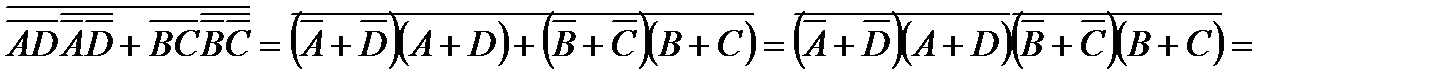
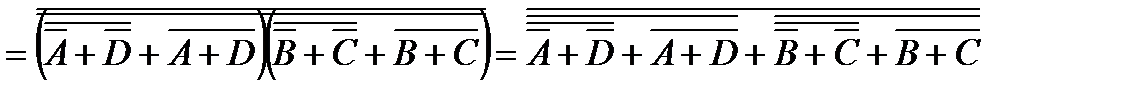. (8)

Комбинационная схема по логическому уравнению (8) в базисе ИЛИ-НЕ показана на рис.2, б.

Проведем логический синтез схем построенных по уравнениям (7) и (8) в САПР ПЛИС Quartus II. Файл отчета в Quartus II, после логического синтеза имеет вид (булева функция реализуется на таблицах перекодировок LUT):

A1L7 = C & B & (D $!A) #!C &!B & (D $!A);

C = INPUT();

B = INPUT();

D = INPUT();

A = INPUT();

FF = OUTPUT(A1L7);

DD = OUTPUT(A1L7);

Представим полученную информацию в привычном для нас виде: .

Из отчета видим, что схемы представленные на рис.2, построенные по различным логическим уравнениям тождественны.

Осуществим функциональное моделирование (без учета реальных задержек распространения сигналов в ПЛИС APEX) с использованием САПР Quartus II и проверим правильность построения таблицы истинности (табл.1). Для осуществления функционального моделирования необходимо в меню Processings/Simulator Settings закладка Mode выбрать режим симулирования Functional. В противном случае, по умолчанию, будет осуществлено временное моделирование с учетом задержек распространения сигналов (Timing) и на временных диаграммах возможно появление выбросов (от английского слова Glitch).

Переберем все комбинации входных сигналов, когда на выходе функции появляется 1. Результаты моделирования представлены на рис.3. Сравнивая табл.1 и результаты моделирования представленные на рис.3 видим, что комбинационная схема работает правильно.

Табл.1

Таблица истинности для булевого выражения

Nпп											f

Рис.1. Комбинационная схема по заданному логическому уравнению (1) и его минимизированным решениям (4) и (5) в схемотехническом редакторе САПР ПЛИС Quartus II

Рис.2. Комбинационная схема по заданному логическому уравнению (7) в базисе И-НЕ (а) и по заданному логическому уравнению (8) в базисе ИЛИ-НЕ (б) в схемотехническом редакторе САПР ПЛИС Quartus II