Оператор безусловного перехода

Оператор безусловного перехода позволяет изменить обычный после­довательный порядок выполнения операторов и непосредственно перейти к нужному опера­тору, предварительно помеченному меткой.

Структура такого оператора:

GOTO < метка >;

где GOTO - ключевое слово, обозначающее перейти к < метке >,

< метка > является произвольным идентификатором, который позволяет пометить любой оператор в программе и потом ссылаться на него.

Оператор от метки отделяется двоеточием. В языке Pascal ABC допускается использовать в качестве метки также целое число без знака.

Пример:

LABEL m1, loop;

VAR a, b, c, d: word;

BEGIN

m1: a: = b+c*d;

...

goto m1;

loop: END.

Все использованные в программе метки должны быть описаны в разде­ле описаний программы с указанием ключевого слова “LABEL”. Описанные в этом операторе метки обязательно должны быть использованы в программе.

Метки, описанные в функции или процедуре, локализуются только в ней, передача управления извне процедуры на метку внутри ее невозмож­на. С помощью оператора GOTO не рекомендуется осуществлять переход во внутреннюю часть сложного оператора (цикла, составного оператора). Запрещается переход с одной альтернативной части (ветви) сложного опе­ратора на другую.

Современная технология структурного программирования основана на принципе программирования без GOTO. Считается, что злоупотребление этими операторами затрудняет чтение программы, усложняет ее отладку.

Тем не менее, в некоторых случаях использование оператора перехода мо­жет упростить программу. Обычно GOTO используется для досрочного выхо­да из любого сложного оператора или вложенных операторов цикла.

 

Пример и задания с оператором IF

Пример. Вычислить значения функции y(x) в зависимости от интервала, в который попадает аргумент x.

Для xÎ [-10,5]

 

где а = 1. 5, b = 0. 5.

Алгоритм представлен на рисунке 1.

Рисунок 1 – Алгоритм программы

 

 

Напишем программу, соответствующую схеме алгоритма (рисунок 1):

Program Lr2;

Label m1, 10;

Const A = 1.5; B = 0.5;

var x, y: real; // переменные вещественного типа

Begin

m1: read(x); // вводим значение переменной x

IF (x < -10) or (x>5) then goto m1;

IF x<0 then begin y: = a*x+b; goto 10 end;

if (x >= 0) and (x<=2) then y: =A*SQR(x)*LN(x+1);

if x>2 then y: = EXP(A*x+1)*COS(B*x);

10: writeln(' x= ', x: 8: 1, ' y= ', y: 8: 2); // вывод значений x и y

Еnd.

Каждому условному оператору в программе соответствует символ “решение” в схеме алгоритма на рисунке 5. Программу можно упростить, используя вложенные условные операторы. Например, если в первом и втором операторах IF добавить их альтернативные части ELSE, тогда в третьем IF условие упростится до вида (x <= 2) и не потребуется последний оператор IF.

Задания к самостоятельному выполнению

Программа 1. Вычислить значение функции в зависимости от интервала, в который попадает вводимый с клавиатуры аргумент:

1. Для t 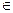[0,3], at²lnt при 1 £ t £ 2,

где a = -0.5,b = 2 z = 1 при t < 1,

e^atcosbt при t > 2,

 

2. Для x 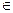[0,4], при x > 2,

где а = 2.3 f = х при 0.3 < x £ 2,

cos(x-a) при x £ 0.3,

 

3. Для x 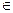[0,7], (a+b)/(e^x+cosx) при 0 £ x < 2.3,

где a = -2.7,b = -0.27 z = (a+b)/(x+1) при 2.3 £ x < 5,

e^x+sinx при 7 ³ х ³ 5,

 

4. Для i 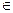[7,12], ai⁴+bi при I < 10,

где a = 2.2,b = 0.3. y = tg(i+0.5) при I = 10,

e²ⁱ+ при I > 10,

 

5. Для x 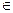[0.9,5], x²-7/x² при x < 1.3,

где a = 1.5 y = ax³+7 при 1.3 £ x < 3,

lg(x+7 ) при x ³ 3,

 

6. Для t 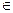[-1.4], при t < 0.1,

где a = 2.1,b = 0.37. z = at+b при 0.1 £ t < 2,

при t ³ 2,

7. Для x 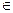[0,6], a e^sinx+2.5 при x < 0.3,

где a = 1.5. y = e^cosx+a при 0.3 £ x < 4,

(sin x)/(a+e^x) при x ³ 4,

 

y =

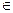8. Для x [1,2], a/x+bx²-c при x £ 1.2,

где a = 1.8,b = -0.5, c = 3.5 (a+bx)/ 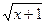при x > 1.2,

 

9. Для t 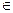[1,5], t при t > a,

где a = 2.5 z = t sin at при t = a,

e^-at cos at при t < a,

 

10. Для x 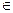[0,4], e^-bx sin bx при x < 2.3,

где a = 1,b = 3 y = сos bx при 2.3 £ x £ 3,

e^-ax cos bx при x ³ 3,

 

11. Для t 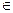[0.5,3], at²-b при t < a,

где a = 1.3, b = 6.5 z = a-b при a £ t £ b,

a t^2/3- при t > b,

 

12. Для x 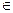[0,2], |e^-2x sin bx| при x >1,

где b = -2.9 y = cos bx при x = 1,

e^-x cos bx при x < 1,

 

13. Для x 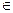[0.5,2] sin (cos ax) при x >1,

где a = -0.8 z = tg ax при x = 1,

a² x при x < 1,

 

14. Для x 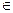[1,2], ln bx - 1/(bx+1) при x < 1.3,

где b = 1.3 y = bx + 1 при 1.3 ³ x ³ 1.7,

ln bx +1/(bx+1) при x > 1.7,

 

15. Для x 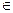[-1,1], ax²+bx^2/3 при x < 0.1,

где a = 2.5,b = -0.9 z = a x² при x = 0.1,

b x^2/3 при x > 0.1.

 

Программа 2.

1. Ввести координаты точки (x, y). Напечатать, в каком квадранте или на какой оси координат находится эта точка.

2. Ввести радиусы R₁, R₂ и высоту. Вычислить объем усеченного конуса: , где S – площадь оснований. Если R₁ = R₂ – объем и площадь цилиндра, если R₁ = 0 или R₂ = 0 – объем (hπr²) и площадь πr(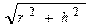) поверхности конуса.

3. Ввести с клавиатуры цифру. Определить, какой системе счисления она может принадлежать.

4. Ввести число. Определить, делится ли оно нацело на два, три или на пять.

5. Ввести a, b, h. Если h = 0, вычислить площадь прямоугольника; при a = b, найти площадь квадрата; в противном случае подсчитать площадь трапеции.

6. Наибольшее из 3-х различных значений переменных вещественного типа Х, У, Z уменьшить на 0.3.

7. Ввести три числа: А, В и С. Вычислить: D = max (A+С, B², C+В);

8. Даны 3 целых числа. Найти среднее из них. Средним назовем число, которое больше наименьшего из данных чисел, но меньше наибольшего.

9. Вычислить значение переменной d=a+в, если а – нечетное, и d=a×в, если а –четное, где а и в целые числа.

10. Найти произведение двух наибольших из трех введенных с клавиатуры чисел.

11. Ввести три числа: а, в и с. Вычислить: К = МАХ (а+в, в·с, в²)

12. Ввести два числа: а и в. Вычислить значение с=а+в, если а – четное и с=а*в, если а – нечетное.

13. Даны Х # У. Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным произведением.

14. Если целое число М делится нацело на целое число N, то вывести частное от деления, иначе вывести сообщение «М на N не делится».

15. Найти:

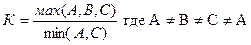
16. Найти: .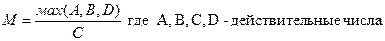

17. Даны целые числа А, В, С. Если А ≤ В ≤ С, то все числа заменить их квадратами, если А > В > С, то каждое число заменить наибольшим из них, в противном случае сменить знак каждого числа.

18. Составить программу нахождения произведения двух наибольших из трех введенных с клавиатуры чисел.

19. Составьте программу, которая из трех введенных с клавиатуры чисел возводит в квадрат положительные, а отрицательные оставляет без изменения.

20. Составьте программу вычисления выражения: МАХ (Х+У+Z, X·Y·Z)+3

21. Составьте программу вычисления выражения: MIN (X2 +Y2, Y2 + Z2, X2+Z2) – 4

22. Составьте программу вычисления выражения: MAX (X·Y, Y·Z, X·Z) +20

23. Составьте программу вычисления выражения: MIN (X2, Y·Z, Z2) ·15

24. Составьте программу вычисления выражения: MAX (X·Z-Y, Z·Y-X, X·Y-Z) + 10

25. Составьте программу вычисления выражения: MIN (X·Z·Y, Y2, Z2) ·X·Z·Y

26. Составьте программу, заменяющую большее из двух данных чисел модулем суммы, а меньшее – модулем полуразности этих чисел.

27. Составьте программу, заменяющую большее из двух данных чисел модулем произведения, а меньшее – модулем разности этих чисел.

28. Составьте программу, заменяющую большее из двух данных чисел удвоенным произведением, а меньшее – модулем полусуммы этих чисел.

29. Составьте программу расположения трех чисел в порядке убывания.

30. Составьте программу расположения трех чисел в порядке возрастания.