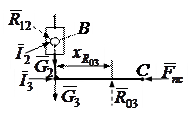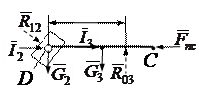ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Методические указания по выполнению контрольных работ
для студентов заочной формы обучения
специальности 150200 «Автомобили и автомобильное хозяйство»
Составитель Н.П. Курышкин
Утверждены на заседании кафедры
Протокол №2 от 01.11.2014
Рекомендованы к печати учебно-
методической комиссией
специальности 150200
Протокол № 3 от 14.11.2014
Электронная копия находится
в библиотеке главного корпуса
КузГТУ
Кемерово 2014
ОБЩИЕ УКАЗАНИЯ
Решению задач контрольных работ должна предшествовать самостоятельная проработка разделов курса теории механизмов и машин. Ниже будут даны ссылки на соответствующие разделы курса, которые необходимо изучить перед решением задач.
Контрольные работы выполняются в ученических тетрадях. Для замечаний проверяющего на каждой странице необходимо оставлять поля шириной не менее 30 мм. Описание решения задач должно быть достаточно подробным, как в приведённых примерах. Графические построения необходимо выполнять карандашом на отдельных листах формата А4 или А3. Листы вклеиваются в тетрадь.
УКАЗАНИЯ К ЗАДАЧАМ КОНТРОЛЬНОЙ РАБОТЫ № 1
Указания к задаче 1
Перед решением задачи 1 изучите раздел «структура механизмов» [1, с. 9…31; 2, с. 21…53]. Вопросы синтеза механизмов без избыточных связей недостаточно освещены в этих учебниках, поэтому воспользуйтесь учебным пособием [5, с. 160…165].
Решение задачи следует начать с вычерчивания структурной схемы рычажного механизма (без учёта размеров звеньев) в двух проекциях. Изучите вид движения всех звеньев и выявите основную функцию механизма как преобразователя движения входного звена в требуемое движение выходного звена. Во всех вариантах входным звеном является кривошип. Он совершает вращательное движение (показан своей координатой j1). Выходное звено (последнее звено цепи, начиная от входного) совершает либо вращательное, либо поступательное движение, в зависимости от варианта схемы.
Все приведённые в задаче механизмы имеют избыточные связи, число которых определяется по структурной формуле:
 , (1)
, (1)
где w – число степеней свободы механизма;
s – суммарное число связей во всех кинематических парах;
n – число звеньев, не считая стойку.
Число степеней свободы механизма определяется последовательным фиксированием (замораживанием) его линейных и угловых координат, например j1. Замораживание одной координаты отнимает у механизма одну степень свободы, поэтому если других нет, то w = 1. Если какие-либо звенья остаются подвижными, то необходимо продолжать замораживание их координат до тех пор, пока механизм полностью не потеряет подвижность. Число степеней свободы w будет равно числу замороженных координат.
Для того чтобы найти суммарное число s связей во всех кинематических парах, необходимо определить это число в каждой из них. Это делается с помощью таблицы [1, с. 31; 2, с. 13,14].
После того, как определено число избыточных связей, их необходимо устранить алгебраическим методом. Для этого приравнивают к нулю левую часть формулы (1), а параметры правой части подбирают так, чтобы обеспечить этот ноль. Задача имеет большое число решений. Для получения единственного решения число степеней свободы w и число подвижных звеньев n задают, оставляя их без изменения. Тогда единственное неизвестное  . Это – необходимое число связей. Его раскладывают во всех возможных вариантах по существующим кинематическим парам и, остановившись на одном из этих вариантов, строят структурную схему. Результат построения проверяют по двум критериям. Во-первых, новый механизм должен быть кинематически эквивалентным исходному, т.е. сохранить существующее ранее преобразование движения. Во-вторых, число степеней свободы нового механизма должно быть равно заданному.
. Это – необходимое число связей. Его раскладывают во всех возможных вариантах по существующим кинематическим парам и, остановившись на одном из этих вариантов, строят структурную схему. Результат построения проверяют по двум критериям. Во-первых, новый механизм должен быть кинематически эквивалентным исходному, т.е. сохранить существующее ранее преобразование движения. Во-вторых, число степеней свободы нового механизма должно быть равно заданному.
Поясним это на примере. Пусть необходимо определить число избыточных связей кривошипно-ползунного механизма (рис. 1, а) и устранить их алгебраическим методом.
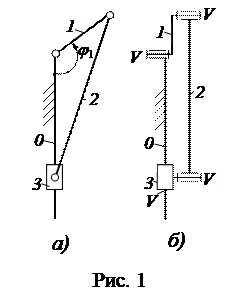 Решение. С целью более наглядного представления структуры механизма изобразим вторую проекцию его схемы (рис. 1, б). Из схемы видно, что основная функция механизма заключается в преобразовании вращательного движения кривошипа 1 в прямолинейное возвратно-поступательное движение ползуна 3. Для определения числа степеней свободы механизма зафиксируем координату.φ1 кривошипа. При этом все звенья механизма потеряют подвижность, следовательно, w = 1.
Решение. С целью более наглядного представления структуры механизма изобразим вторую проекцию его схемы (рис. 1, б). Из схемы видно, что основная функция механизма заключается в преобразовании вращательного движения кривошипа 1 в прямолинейное возвратно-поступательное движение ползуна 3. Для определения числа степеней свободы механизма зафиксируем координату.φ1 кривошипа. При этом все звенья механизма потеряют подвижность, следовательно, w = 1.
По таблице [1, с. 31; 2, с. 13,14] определим числа связей во всех кинематических парах (на рис. 1, б они проставлены римскими цифрами). Все четыре кинематические пары имеют по пять связей, поэтому суммарное число связей: 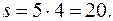 По формуле (1) число избыточных связей
По формуле (1) число избыточных связей
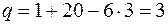 .
.
По условию задачи механизм не должен иметь избыточных связей, поэтому, приравнивая  и подставляя w = 1, n = 3, получим требуемое суммарное число связей s = 6 n – w + q = 6·3 – 1 + 0 = 17. Распределив эти связи по четырём кинематическим парам, получим три варианта их раскладки: V, V, V, II; V, V, IV, III; V, IV, IV, IV. Перестановки не учитываются, т. к. их можно сделать при построении схемы.
и подставляя w = 1, n = 3, получим требуемое суммарное число связей s = 6 n – w + q = 6·3 – 1 + 0 = 17. Распределив эти связи по четырём кинематическим парам, получим три варианта их раскладки: V, V, V, II; V, V, IV, III; V, IV, IV, IV. Перестановки не учитываются, т. к. их можно сделать при построении схемы.
Для решения задачи достаточно выбрать любое сочетание и начертить соответствующую ему структурную схему механизма.
На рис. 2 представлены три структурные схемы, соответствующие варианту V, V, IV, III. Схема на виде а) – правильная, на виде б) и в) – неправильные. Механизм на виде б) потерял свою основную функцию – звено 3 не может двигаться вертикально. Механизм на виде в) имеет две степени свободы (w= 2). Вторая степень свободы – поворот звена 3 вокруг вертикальной оси ( Dj3) – появилась в результате удаления не избыточной, а необходимой связи, влияющей на кинематику механизма.
Dj3) – появилась в результате удаления не избыточной, а необходимой связи, влияющей на кинематику механизма.

Рис. 2
Указания к задаче 2
Перед решением задачи 2 изучите раздел «кинематический анализ зубчатых механизмов» [1, с. 52…57; 2, с. 142, 143, 151…172].
Решение задачи начните с вычерчивания в масштабе кинематической схемы планетарного механизма в двух проекциях (рис. 3, а, б).

По условию задачи все колёса изготовлены без смещения производящего контура, поэтому диаметры di (рис. 3, б)принимаются равными диаметрам их делительных окружностей:
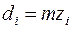 ,
,
где zi – число зубьев i –го колеса; m – модуль зубчатых колёс. По условию задачи т = 5 мм.
После вычерчивания кинематической схемы изучите структуру механизма, проследите за передачей движения от входного колеса 1 к водилу Н. Покажите направления угловых скоростей ω i всех подвижных звеньев. Сделайте это, как показано на рис. 3, б.
Передаточное отношение u 1 H определяется по формуле Виллиса:
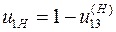 , (2)
, (2)
где  ‑ передаточное отношение от первого колеса к третьему в обращённом движении, т.е. при закреплённом водиле Н и освобождённом колесе 3 (говоря иначе, после перестановки механизма на водило).
‑ передаточное отношение от первого колеса к третьему в обращённом движении, т.е. при закреплённом водиле Н и освобождённом колесе 3 (говоря иначе, после перестановки механизма на водило).
После перестановки на водило передача превращается в обыкновенную с неподвижными осями (рис. 3, в), для неё:
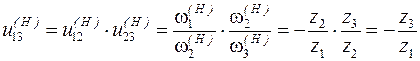 . (3)
. (3)
Передаточное отношение  отрицательное потому, что колёса
отрицательное потому, что колёса
1, 2 вращаются в разные стороны и их скорости  ,
,  имеют разные знаки. Передаточное отношение
имеют разные знаки. Передаточное отношение  положительное потому, что скорости
положительное потому, что скорости  и
и  направлены в одну и ту же сторону и, следовательно, имеют одинаковые знаки.
направлены в одну и ту же сторону и, следовательно, имеют одинаковые знаки.
Следует иметь в виду, что индексы при u указывают номера звеньев, а не зубчатых колёс. Это замечание несущественно для рассматриваемого примера, но важно для передач, предлагаемых в контрольной работе. В этих передачах сателлит состоит из двух зубчатых колёс, сидящих на одном валу. Сателлит является звеном № 2, его колёса имеют числа зубьев z2 и z2´. При таких обозначениях  . Знак устанавливается по картине, подобной той, что изображена на рис. 3, в.
. Знак устанавливается по картине, подобной той, что изображена на рис. 3, в.
Результат, полученный по формуле (2), проверяют графически. Для этого на второй проекции строят картину линейных скоростей (рис. 4, а) и, отдельно, картину угловых скоростей (рис. 4, б).

Рис.4
Для построения картины линейных скоростей (рис. 4, а) проводят вектор, изображающий в некотором неизвестном масштабе скорость 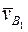 и
и  общей точки В центрального колеса 1 и сателлита 2. Соединив конец этого вектора с центром вращения колеса 1 – точкой А – получают линию распределения скоростей (л.р.с.) всех его точек, лежащих на радиусе АВ. Для построения л.р.с. сателлита (блока сателлитов) определяют положение мгновенного центра его вращения. Нахождение этой точки является ключевым моментом при построении картины линейных скоростей. Мгновенным центром вращения всегда является точка касания сателлита (блока сателлитов) с неподвижным колесом, в нашем примере – это точка D. Соединив конец вектора
общей точки В центрального колеса 1 и сателлита 2. Соединив конец этого вектора с центром вращения колеса 1 – точкой А – получают линию распределения скоростей (л.р.с.) всех его точек, лежащих на радиусе АВ. Для построения л.р.с. сателлита (блока сателлитов) определяют положение мгновенного центра его вращения. Нахождение этой точки является ключевым моментом при построении картины линейных скоростей. Мгновенным центром вращения всегда является точка касания сателлита (блока сателлитов) с неподвижным колесом, в нашем примере – это точка D. Соединив конец вектора  с точкой D, получают линию распределения скоростей сателлита 2. С помощью этой линии определяют скорость центра сателлита С 2. Такую же скорость имеет конец С водила Н. Соединяя конец вектора
с точкой D, получают линию распределения скоростей сателлита 2. С помощью этой линии определяют скорость центра сателлита С 2. Такую же скорость имеет конец С водила Н. Соединяя конец вектора  с центром вращения А водила, получают л.р.с. водила. На этом построение картины распределения линейных скоростей закончено.
с центром вращения А водила, получают л.р.с. водила. На этом построение картины распределения линейных скоростей закончено.
Для построения картины угловых скоростей проводят две взаимноперпендикулярные прямые (рис. 4, б). На вертикальной прямой откладывают произвольный отрезок ab. Из точки а проводят лучи, параллельные линиям распределения скоростей. Эти лучи отсекают на горизонтальной прямой отрезки, пропорциональные угловым скоростям соответствующих звеньев. Искомое передаточное отношение:
 . (4)
. (4)
Угловые скобки указывают на то, что речь идёт о длине отрезков, изображающих величины, заключённые в эти скобки. Длины отрезков выражают в миллиметрах. Если отрезки 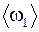 и
и  окажутся по разные стороны от перпендикуляра ab, то
окажутся по разные стороны от перпендикуляра ab, то  будет отрицательным. Передаточное отношение, полученное по формуле (4), сравнивают с полученным по формуле (2). На этом решение задачи заканчивается.
будет отрицательным. Передаточное отношение, полученное по формуле (4), сравнивают с полученным по формуле (2). На этом решение задачи заканчивается.
Указания к задаче 3
Задача 3 относится к геометрии эвольвентного зацепления. Изучите раздел «синтез зубчатых механизмов» [1, с. 179…195, 2, с. 416…460, 5, с. 25…54].
Зубчатые колёса изготавливают в основном методом обката (огибания). При этом инструмент в виде зубчатого колеса или зубчатой рейки катится по производимому колесу Инструмент первого типа называется далее производящим колесом (ПК), инструмент второго типа – производящей рейкой (ПР). Чтобы изготовить эвольвентное колесо, ПК должно быть тоже эвольвентным (с эвольвентным профилем зубьев), а ПР должна быть прямобочной (с прямолинейным профилем зубьев). Последнее объясняется тем, что при увеличении числа зубьев колеса до бесконечности, эвольвента превращается в прямую. Таким образом, прямобочная рейка – это частный случай эвольвентного колеса. Конфигурация и параметры ПР стандартизованы (рис. 5). На ПР имеется базовая линия, которая называется делительной прямой (ДП). На ней толщина зуба и ширина впадины одинаковые.
В половине вариантов третьей задачи рассматривается геометрия зацепления производящей рейки с производимым колесом. Это зацепление называется станочным.

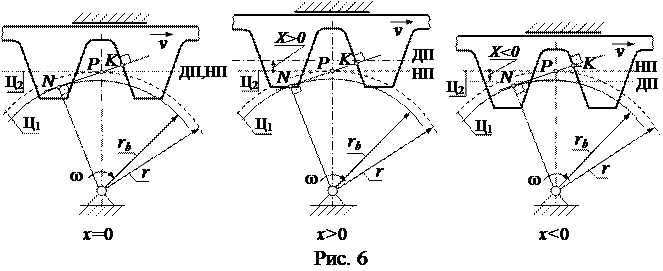 Пусть требуется изготовить зубчатое колесо с числом зубьев z производящей рейкой с модулем т. Чтобы получить заданное z, необходимо определить соотношение скоростей ω и v производимого колеса и производящей рейки (рис. 6). Очевидно, что на производимом колесе должно «отпечататься» целое число зубьев и, следовательно, целое число стандартных шагов р. На каждой окружности производимого колеса, шаг имеет свою величину: чем больше радиус этой окружности, тем больше шаг. Из всех этих окружностей имеется лишь одна, на которой шаг р «отпечатался» с производящей рейки без искажения. Эта окружность называется делительной. Записывая её длину через шаг L = рz (р = πт)и через радиус L = 2π r, и приравнивая друг к другу правые части полученных выражений, получают формулу определения радиуса r = mz/2. Скопировать шаг р на делительную окружность можно единственным способом – прокатить по ней без скольжения делительную прямую рейки (рис. 6, а) или любую другую прямую, параллельную ДП рейки (шаг по этой прямой тоже равен р) (рис. 6, б, в). Линии взаимного обката называются центроидами. Центроида Ц2 называется начальной прямой (НП). Точка касания Р центроид зацепления называется полюсом зацепления.
Пусть требуется изготовить зубчатое колесо с числом зубьев z производящей рейкой с модулем т. Чтобы получить заданное z, необходимо определить соотношение скоростей ω и v производимого колеса и производящей рейки (рис. 6). Очевидно, что на производимом колесе должно «отпечататься» целое число зубьев и, следовательно, целое число стандартных шагов р. На каждой окружности производимого колеса, шаг имеет свою величину: чем больше радиус этой окружности, тем больше шаг. Из всех этих окружностей имеется лишь одна, на которой шаг р «отпечатался» с производящей рейки без искажения. Эта окружность называется делительной. Записывая её длину через шаг L = рz (р = πт)и через радиус L = 2π r, и приравнивая друг к другу правые части полученных выражений, получают формулу определения радиуса r = mz/2. Скопировать шаг р на делительную окружность можно единственным способом – прокатить по ней без скольжения делительную прямую рейки (рис. 6, а) или любую другую прямую, параллельную ДП рейки (шаг по этой прямой тоже равен р) (рис. 6, б, в). Линии взаимного обката называются центроидами. Центроида Ц2 называется начальной прямой (НП). Точка касания Р центроид зацепления называется полюсом зацепления.
При взаимном обкатывании скорости точек, лежащих на делительной окружности, равны скорости рейки. Отсюда  , и по скорости ω можно вычислить скорость v, требуемую для получения заданного z, что и требуется.
, и по скорости ω можно вычислить скорость v, требуемую для получения заданного z, что и требуется.
На рис. 6 производящая рейка изображена без скруглённой части зуба. Это сделано потому, что скруглённая часть не участвует в образовании эвольвенты. Через полюс Р проходит линия зацепления PN. Она является общей нормалью к сопряжённым профилям в точке их касания K (профиль зуба производимого колеса на рисунке не показан). Как отмечено выше, профиль зуба производящей рейки прямолинейный, поэтому нормаль к профилю превращается в перпендикуляр к нему. Линия зацепления одновременно является касательной к основной окружности радиуса rb.
Как видно из рис. 6, различные положения ПР относительно начальной прямой определяются смещением X = xm, где x – коэффициент смещения. Смещение вверх считается положительным (x> 0), а смещение вниз – отрицательным (x< 0). Необходимо ещё раз отметить, что во всех трёх вариантах делительная и основная окружности остаются неизменными и, следовательно, профилируется одна и та же эвольвента. Только для профиля зуба колеса используются различные её участки (рис. 7).
 |
Рис. 7
Таким образом, при заданном числе зубьев и модуле производимого колеса варьированием коэффициента смещения x можно в определённых пределах менять как форму зуба, так и радиальные размеры зубчатого колеса.
В некоторых вариантах задачи 3 предлагается достроить картину двух эвольвентных колёс с заданным профилем зубьев. Построив общую нормаль в точке касания сопряжённых профилей, находят полюс зацепления как точку пересечения этой нормали с линией центров. Через полюс зацепления проводят начальные окружности. Эти окружности являются центроидами и, следовательно, катятся друг по другу без скольжения, а отношение их радиусов есть передаточное отношение зацепления. Общая нормаль касается основных окружностей. На этом основании строят основные окружности. Для эвольвентного зацепления общая нормаль является линией зацепления (траекторией абсолютного движения точки касания зубьев). Линия зацепления ограничена точками касания общей нормали с основными окружностями. Фактически зубья контактируют на меньшем участке линии зацепления, называемом активной частью линии зацепления. Границами активной части являются точки пересечения линии зацепления с окружностями вершин зубьев.
Угол зацепления aw – это угол между линией зацепления и перпендикуляром, восстановленном к линии центров в полюсе зацепления. В зависимости от того, с каким смещением изготовлены зубчатые колёса (см. рис. 7), возможны три варианта: aw< 20o, aw= 20o, aw> 20o. Если в зацеплении находятся колёса, изготовленные с нулевым смещением или зацепление является равносмещённым (x 1=– x 2), то начальные окружности совпадают с делительными.
УКАЗАНИЯ К ЗАДАЧАМ КОНТРОЛЬНОЙ РАБОТЫ № 2
Указания к задаче 1
Перед решением задачи 1 изучите раздел «кинематический анализ механизмов» и в частности «кинематический анализ рычажных механизмов методом планов скоростей и ускорений» [1, с. 82…95, 2, с. 35…43]. Этот метод базируется на представлении структуры плоских механизмов по Ассуру. Поэтому обязательным является предварительное изучение раздела «структура механизмов» и, в частности, параграфа «группы Ассура» (они же структурные группы) [1, с. 28…31, 2, с. 53…66, 5, с. 68…71].
Решение задачи 1 начинают с вычерчивания схемы рычажного механизма в масштабе. Все построения (схему механизма, планы скоростей и ускорений) рекомендуется выполнять на отдельном листе миллиметровой бумаги формата А3 или А4, который затем вклеивают в контрольную работу. Далее механизм раскладывают на группы Ассура. Разложение начинают с выделения начальной системы – стойки с кривошипом АВ. Оставшаяся группа звеньев 2,3 является группой Ассура. Такие группы относят ко второму классу. Разложение на группы Ассура необходимо потому, что они, обладая определённостью положения относительно мест присоединения, являются кинематически определимыми системами. Кинематическая определимость означает, что при известных скоростях и ускорениях мест присоединения группы, всегда можно определить скорости и ускорения точек внутри группы Ассура. Эти величины определяют графическим решением векторных уравнений, составленных на основании разложения движения каждого из звеньев группы на переносное и относительное. Переносным (переносящим) считается движение подвижной системы координат (ПСК) относительно неподвижной, связанной со стойкой. ПСК вводится в механизм искусственно. После разложения движения уравнения скоростей и ускорений выглядят так:

где  – искомая абсолютная скорость и абсолютное ускорение переносимой точки;
– искомая абсолютная скорость и абсолютное ускорение переносимой точки; 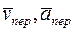 – скорость и ускорение той точки ПСК, которая в данный момент совпадает с переносимой точкой;
– скорость и ускорение той точки ПСК, которая в данный момент совпадает с переносимой точкой;  – скорость и ускорение переносимой точки относительно ПСК;
– скорость и ускорение переносимой точки относительно ПСК; 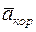 – ускорение Кориолиса. Его модуль
– ускорение Кориолиса. Его модуль
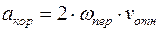 , (5)
, (5)
где  – угловая скорость ПСК. Напомним правило определения направления ускорения Кориолиса – оно определяется поворотом вектора относительной скорости на 90˚ в сторону угловой скорости переносного движения (рис. 8, а).
– угловая скорость ПСК. Напомним правило определения направления ускорения Кориолиса – оно определяется поворотом вектора относительной скорости на 90˚ в сторону угловой скорости переносного движения (рис. 8, а).
 Необходимо также вспомнить некоторые сведения из теоретической механики для вращательного движения (см. рис. 8, б) независимо от того, какое оно – абсолютное, переносное или относительное: 1) скорость
Необходимо также вспомнить некоторые сведения из теоретической механики для вращательного движения (см. рис. 8, б) независимо от того, какое оно – абсолютное, переносное или относительное: 1) скорость  перпендикулярна АВ и направлена в сторону угловой скорости ω; 2) ускорение
перпендикулярна АВ и направлена в сторону угловой скорости ω; 2) ускорение 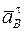 перпендикулярно АВ и направлено в сторону углового ускорения ε; 3) ускорение
перпендикулярно АВ и направлено в сторону углового ускорения ε; 3) ускорение 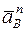 направлено к центру вращения.
направлено к центру вращения.
Для того чтобы векторные уравнения решались, разложение движения выполняют, руководствуясь следующим правилом: движение переносимого звена относительно ПСК должно быть простейшим – поступательным или вращательным. В общем случае, когда места присоединения обоих звеньев группы Ассура подвижны, раскладывают движение каждого из её звеньев. В частных случаях достаточно разложения движения одного звена. Во всех вариантах задачи 1 вам встретятся только частные случаи. В табл. 1 приведены все модификации групп Ассура второго класса и рассмотрены различные варианты присоединения этих групп к начальному механизму. Здесь же показано разложение движения и записаны векторные уравнения для определения скоростей и ускорений точек внутри групп Ассура.
В случаях 1, 3, 4 (табл.1) в уравнениях отсутствует ускорение Кориолиса. Это объясняется тем, что переносное движение здесь поступательное. При поступательном движении  и, следовательно, по формуле (5)
и, следовательно, по формуле (5)  .
.
Таблица 1
Группы Ассура и векторные уравнения
| № | Группа Ассура | Разложение абсолютного движения… | Скорости и ускорения |

| звена 2 на поступательное с Bxy и вращательное относит. Bxy. |


| |

| звена 3 на плоско-парал. с x2y2 и поступательное. относит. x2y2. |
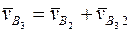

| |
| 2a | 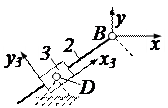
| звена 2 на поступ. с Bxy и вращат. относит. Bxy, а также на вращательное с x3y3 и поступат. относит. x3y3. | 


|

| звена 2 на поступательное. с Bxy и вращательное относит. Bxy. |


| |
| 3а | 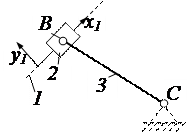
| звена 2 на вращательное с x1y1 и поступательное относит. x1y1. |


|
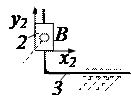
| звена 3 на поступательное с x2y2 и поступат. относит. x2y2. |
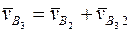

| |

| звена 2 на вращательное с x1y1 и поступат. относит. x1y1. |
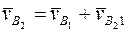

|

Приведённые в табл. 1 пояснения по разложению абсолютного движения помогут в определении направлений и линий действия векторов, входящих в уравнения. Именно с этого начинается их графическое решение – построение планов скоростей и ускорений.
П р и м е р. Для кулисного механизма, изображённого на рис. 9, а, дано: lAB, lBC, 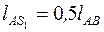 ,
,  , φ1, ω1, ε1. S1 и S2 – центры масс звеньев. Схема вычерчена в положении, заданном углом φ1, в произвольно выбранном масштабе (масштабный коэффициент схемы μ l, м/мм). Требуется определить:
, φ1, ω1, ε1. S1 и S2 – центры масс звеньев. Схема вычерчена в положении, заданном углом φ1, в произвольно выбранном масштабе (масштабный коэффициент схемы μ l, м/мм). Требуется определить:  ,,
,, 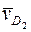 ,
, 
 ,
,  , ω2, ω3,
, ω2, ω3,
 ,
,  ,
,  ,
, 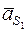 ,
,  , ε2, ε3.
, ε2, ε3.
Согласно рекомендациям, изложенным выше, разложим механизм на группы Ассура. Для этого выделим начальную систему, состоящую из стойки 0 и кривошипа 1 (рис. 9, б). Остаётся двухповодковая группа Ассура, состоящая из звеньев 2 и 3 (рис. 9, в).
Определим скорости в начальной системе:
1) скорость точки В
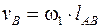 , м/с; (6)
, м/с; (6)
она направлена перпендикулярно АВ в сторону ω1 (см. рис. 8, б);
2) скорость точки S1 равна половине vB и направлена в ту же сторону.
Далее переходим к группе Ассура. По табл. 1 выбираем соответствующий вариант присоединения структурной группы к стойке начальной системы. Для нашей задачи – это вариант 2а. Записываем соответствующее уравнение из табл.1 (пояснения по разложению движений см. в той же таблице):
 , (7)
, (7)
где 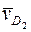 – скорость точки D2 относительно стойки;
– скорость точки D2 относительно стойки; 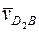 – скорость точки D2 относительно ПСК Bxy.
– скорость точки D2 относительно ПСК Bxy.
Скорости в уравнении (7), для большей наглядности, дополняем обозначением направлений их линий действия, а также подчёркиваниями – одной чертой, если известно только направление линии действия вектора, двумя чертами, если известен ещё и модуль вектора. Такие дополнения позволяют быстро оценить разрешимость векторного уравнения. Так в уравнении (7) крайние векторы подчёркнуты одной чертой (их модули неизвестны), следовательно, это уравнение разрешимо (при трёх и более неизвестных уравнение не решается). Решаем его графически – строим план скоростей рядом с кинематической схемой механизма (рис. 10, а). С этой целью из произвольно выбранного полюса р (рис. 10, б) откладываем произвольной длины вектор pb перпендикулярно АВ. Вычисляем масштабный коэффициент будущего плана скоростей:
 , м·с-1/мм.
, м·с-1/мм.
Согласно уравнению (7), из конца вектора pb, проводим линию, перпендикулярную DВ, а из полюса р – линию, параллельную DВ. Получаем точку пересечения этих линий d2. Векторы pd2 и bd2 выражают скорости 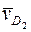 и
и 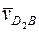 , соответственно. Модули этих векторов вычисляем по формуле:
, соответственно. Модули этих векторов вычисляем по формуле:
 , (8)
, (8)
где  – выраженная в миллиметрах длина отрезка, изображающего скорость vi. Например
– выраженная в миллиметрах длина отрезка, изображающего скорость vi. Например  , м/с. Скорости точек C, S2 определяем по теореме подобия, так как скорости двух точек кулисы 2 найдены. Для этого достаточно на линии bd2 плана скоростей найти положение точек c и s2 такое, какое они занимают на кулисе. Из пропорции
, м/с. Скорости точек C, S2 определяем по теореме подобия, так как скорости двух точек кулисы 2 найдены. Для этого достаточно на линии bd2 плана скоростей найти положение точек c и s2 такое, какое они занимают на кулисе. Из пропорции 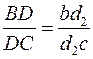 выведем
выведем  . Точки B, D, C лежат на одной прямой. При движении из точки B в D точка C встречается после D. Таким же должно быть взаимное положение точек b, d2, с на плане скоростей. На этом основании найдём положение точки c. Длины отрезков DC и BD снимают со схемы механизма.
. Точки B, D, C лежат на одной прямой. При движении из точки B в D точка C встречается после D. Таким же должно быть взаимное положение точек b, d2, с на плане скоростей. На этом основании найдём положение точки c. Длины отрезков DC и BD снимают со схемы механизма.
Центр масс кулисы S2 находится на середине отрезка BC. Поэтому, разделив отрезок bc на плане скоростей пополам, найдём положение

точки s2. Проведя из точки р векторы pc и ps2 получим скорости  и
и  , соответственно. Модули скоростей вычисляют по формуле (8). На этом план скоростей можно считать построенным.
, соответственно. Модули скоростей вычисляют по формуле (8). На этом план скоростей можно считать построенным.
После определения линейных скоростей перейдём к угловым скоростям звеньев. Угловая скорость кулисы
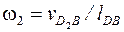 , с–1.
, с–1.
Судя по уравнению (7), вектор 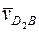 направлен от точки b к точке d2. Переносом вектора
направлен от точки b к точке d2. Переносом вектора 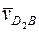 в точку D2 (рис. 10, а) найдём, что он стремится повернуть кулису вокруг точки В против часовой стрелки, туда же направлена и скорость ω2.
в точку D2 (рис. 10, а) найдём, что он стремится повернуть кулису вокруг точки В против часовой стрелки, туда же направлена и скорость ω2.
Кулиса 2 и кулисный камень 3 соединены между собой поступательной кинематической парой, поэтому ω3 = ω2. Причём, как по величине, так и по направлению.
На этом определение линейных и угловых скоростей закончено. Перейдём к ускорениям. Последовательность определения ускорений та же, что и скоростей.
Ускорение точки В кривошипа (рис. 9, б, см. также рис. 8, б)
 , (9)
, (9)
где 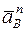 – нормальная составляющая,
– нормальная составляющая, 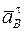 – тангенциальная.
– тангенциальная.
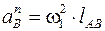 , м/с2,
, м/с2, 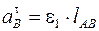 , м/с2.
, м/с2. 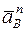 направлено от В к А,
направлено от В к А, 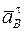 – перпендикулярно АВ и направлено в сторону ε1.
– перпендикулярно АВ и направлено в сторону ε1.
Полное ускорение точки В найдём графически (рис. 10, г). Для этого из полюса π проведём произвольной длины отрезок π n1, изображающий 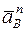 . По формуле
. По формуле 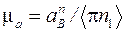 , м·с-2/мм, вычислим масштабный коэффициент будущего плана ускорений. Вычислим длину отрезка n1b, изображающего ускорение
, м·с-2/мм, вычислим масштабный коэффициент будущего плана ускорений. Вычислим длину отрезка n1b, изображающего ускорение 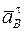 :
: 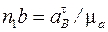 , мм. Отложим n1b из точки n1. Соединив полюс π с точкой b, получим вектор π b, изображающий
, мм. Отложим n1b из точки n1. Соединив полюс π с точкой b, получим вектор π b, изображающий  . Численное значение ускорения точки В найдём по формуле:
. Численное значение ускорения точки В найдём по формуле:  , м/с2. Таким образом, модуль и направление ускорения
, м/с2. Таким образом, модуль и направление ускорения  найдено.
найдено.
Ускорение центра масс S1 кривошипа найдём по теореме подобия. Для этого отметим, что начало и конец ускорения точки А находится в полюсе. Точка S1 расположена на середине АВ. Такое же положение должна занимать точка s1 по отношению к аb. Проведя вектор из π в s1, получим ускорение 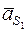 . Как видно по рисунку,
. Как видно по рисунку,  , м/с2.
, м/с2.
Определим ускорения в группе Ассура 2, 3. Начнём с точки D2. Как видно по табл. 1 (строка 2а)
 , (10)
, (10)
где 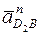 и
и  – нормальная и тангенциальная составляющие ускорения точки D2 относительно системы Bxy;
– нормальная и тангенциальная составляющие ускорения точки D2 относительно системы Bxy;  – ускорение точки D звена 3 (эта точка неподвижна);
– ускорение точки D звена 3 (эта точка неподвижна);  и
и 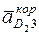 – относительное и кориолисово ускорение точки D2 относительно системы x3y3.
– относительное и кориолисово ускорение точки D2 относительно системы x3y3.
Вычислим 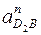 и
и  :
:  , м/с2;
, м/с2;  , м/с2 (
, м/с2 ( ). Укажем снизу уравнений, как сориентированы векторы относительно звеньев. Направление ускорения Кориолиса определим с помощью рис. 10, в. После вычислений остаются неизвестными
). Укажем снизу уравнений, как сориентированы векторы относительно звеньев. Направление ускорения Кориолиса определим с помощью рис. 10, в. После вычислений остаются неизвестными  ,
,  и
и  . Последнее неизвестно ни по величине, ни по направлению. С учётом этого имеем два уравнения с четырьмя неизвестными, из чего следует, что система (10) разрешима.
. Последнее неизвестно ни по величине, ни по направлению. С учётом этого имеем два уравнения с четырьмя неизвестными, из чего следует, что система (10) разрешима.
Графическое решение этой системы (рис. 10, г) заключается в построении из единой точки (полюса π) цепочек векторов, стоящих в правой части уравнений. Вектор  прибавляют последним. Точка пересечения линий действия последних слагаемых даёт решение. На этом основании из конца вектора π b проведём вектор bn2 =
прибавляют последним. Точка пересечения линий действия последних слагаемых даёт решение. На этом основании из конца вектора π b проведём вектор bn2 =  , мм, изображающий ускорение
, мм, изображающий ускорение 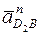 . А из полученной точки n2 проведём линию действия вектора
. А из полученной точки n2 проведём линию действия вектора  . Цепочка векторов второго уравнения начинается в полюсе π вектором π k длиной
. Цепочка векторов второго уравнения начинается в полюсе π вектором π k длиной  , мм. Из полученной точки k проведём линию действия относительного ускорения
, мм. Из полученной точки k проведём линию действия относительного ускорения  . На пересечении линий действия векторов
. На пересечении линий действия векторов  и
и  получим точку d2. Соединив полюс π с точкой d2, получим ускорение точки D2. Численное значение этого ускорения вычислим по формуле:
получим точку d2. Соединив полюс π с точкой d2, получим ускорение точки D2. Численное значение этого ускорения вычислим по формуле:  , м/с2. Аналогично найдём:
, м/с2. Аналогично найдём:  , м/с2;
, м/с2; 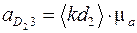 , м/с2.
, м/с2.
Ускорения точек C и S2 определим по теореме подобия. Она применяется также как при определении скоростей (см. выше).
Кинематический анализ закончим определением угловых ускорений звеньев. Угловое ускорение кулисы 2  , с-2. Направление ε2 определим переносом вектора n2d2, выражающего ускорение
, с-2. Направление ε2 определим переносом вектора n2d2, выражающего ускорение  , в точку D2. Этот вектор стремится повернуть звено 2 вокруг точки В против часовой стрелки. Так же направлено и ε2. Угловое ускорение ε3 кулисного камня 3, как и угловая скорость, равно угловому ускорению ε2.
, в точку D2. Этот вектор стремится повернуть звено 2 вокруг точки В против часовой стрелки. Так же направлено и ε2. Угловое ускорение ε3 кулисного камня 3, как и угловая скорость, равно угловому ускорению ε2.
На этом решение задачи 1 закончено.
Указания к задаче 2
Перед решением задачи изучите раздел «силовой анализ механизмов» [1, с. 57…64; 2, с. 215…217, 250…252, 259…270, 272…280, 5, с. 95…104].
Целью силового расчёта является определение реакций в кинематических парах, а также внешних сил (в контрольной работе – момента, приложенного к кривошипу), обеспечивающих заданное движение (заданные ω1 и ε1). Эта цель достигается решением уравнений равновесия звеньев. Использовать уравнения равновесия позволяет принцип Даламбера. Согласно этому принципу, привести систему в искусственное равновесие можно, приложив к звеньям механизма, кроме реально действующих сил, силы инерции. Эти силы искусственно прикладываются к звеньям, на которые на самом деле не действуют. Силы инерции элементарных масс звена приводят к его центру масс и представляют главным вектором  и главным моментом
и главным моментом  . Их модули
. Их модули
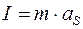 , Н;
, Н; 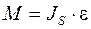 , Н·м; (11)
, Н·м; (11)
m – масса звена, кг; aS – ускорение центра масс звена, м/с2; JS – момент инерции звена относительно центра масс, кг·м2; ε – угловое ускорение звена, с-2.
 Главный вектор сил инерции прикладывают к центру масс S (рис. 11) и направляют противоположно
Главный вектор сил инерции прикладывают к центру масс S (рис. 11) и направляют противоположно  . Главный момент направляют противоположно ε.
. Главный момент направляют противоположно ε.
Для упрощения системы сил инерции избавляются от главного момента  . Это делают параллельным смещением главного вектора на расстояние
. Это делают параллельным смещением главного вектора на расстояние
x=M/I, м. (12)
Смещают вектор  так, чтобы он стремился повернуть звено вокруг центра масс в сторону М.
так, чтобы он стремился повернуть звено вокруг центра масс в сторону М.
В случае поступательного движения звена его угловое ускорение равно нулю и, следовательно, М = 0.
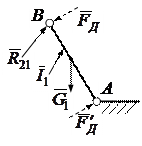
Силовой расчёт механизма, как и кинематический анализ, ведётся по группам Ассура. Эти группы являются статически определимыми системами, т.е. для них число неизвестных сил равно числу независимых уравнений равновесия. Методика расчёта групп Ассура и начальной системы приведена в табл. 2. При этом: направления сил инерции показаны произвольно; под знаком Σ указан номер звена, из равновесия которого составлено соответствующее уравнение; не показаны плечи сил; искомые силы выделены чертой снизу. Кроме этого, искомые реакции в группах Ассура 2 ( ), 2а (
), 2а ( ) и 4 (
) и 4 ( ) не разложены на две составляющие. В этом нет необходимости, так как графическое решение соответствующих уравнений равновесия даёт возможность определить как их модуль, так и направление. На расчётной схеме направление этих реакций показано произвольно.
) не разложены на две составляющие. В этом нет необходимости, так как графическое решение соответствующих уравнений равновесия даёт возможность определить как их модуль, так и направление. На расчётной схеме направление этих реакций показано произвольно.
Таблица 2
| № | Группа Ассура | Методика расчёта | |||
| 1.  : :  .
2. .
2.  : :  .
3. .
3.  : :  .
4. .
4. 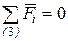 : :  . .
| ||||
|
1.  : :  .
2. .
2. 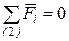 : :  .
3. .
3.  : :  ,
где ,
где  . .
| ||||
| 2a |
|
1.  : :  .
2. .
2.  : :  .
3. .
3. 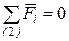 : :  ,
где ,
где 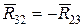 . .
| |||
|
1.  : :  .
2. .
2.  : :
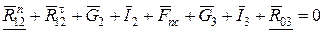 .
3. .
3.  : :  . .
|
Продолжение табл. 2
| № | Группа Ассура | Методика расчёта | |||||
| 3а | 
| 1.  : : 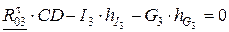 .
2. .
2.  : :
 .
3. .
3. 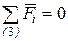 : :  . .
| |||||

| 1. 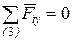 : :  .
2. .
2.  : :  .
3. .
3.  : : 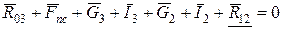 .
4. .
4. 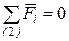 : : 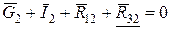 . .
| ||||||
| 1.  : :  .
2. .
2.  : :  .
3. .
3. 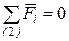 : :  . .
| ||||||
Начальная система
| 1.  : :
 .
2. .
2. 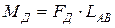 3.
3. 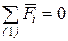 : :  . .
|
Силовой расчёт выполняют в следующей последовательности.
1. В масштабе вычерчивают начальную систему и группу Ассура, как показано на рис. 9, б, в (системы координат не показывают).
Кинематический анализ (планы скоростей и ускорений) и силовой расчёт делают на одном листе.
2. По формулам (13) вычисляют модули главного вектора и главного момента сил инерции каждого звена.
3. К начальному звену и звеньям группы Ассура прикладывают силы инерции, силы тяжести, силу полезного сопротивления Fпс и искомые реакции во внешних кинематических парах.
4. По табл. 2, определяют реакции во всех кинематических парах группы Ассура.
5. Выполняют расчёт начальной системы, для которой определяют уравновешивающий (движущий) момент и реакцию в шарнире кривошипа со стойкой (табл. 2, строка 6).
6. С помощью «рычага» Жуковского ещё раз определяют уравновешивающий (движущий) момент и сравнивают его с моментом, найденным в п. 5. Погрешность расчётов не должна превышать 10%.
П р и м е р. Используя исходные данные и результаты решения задачи 1, выполнить силовой расчёт кулисного механизма (рис. 10, а), если известны: массы звеньев – m 1, m 2, m 3, кг; моменты инерции относительно центров масс JS 1, JS 2, кг·м2; сила полезного сопротивления Fпс, Н, приложенная в точке С.
Вычертим группу Ассура и начальную систему в (рис. 12, а, б) в заданном положении (см. значение угла φ1). В табл. 2 найдём такую же как у нас группу Ассура (строка 2а).
Вычислим силы инерции: 1) кривошипа 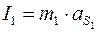 , Н;
, Н;  , Н·м; 2) кулисы
, Н·м; 2) кулисы  , Н;
, Н;  , Н·м; 3) кулисного камня I 3 = 0, M 3 = 0. Приложим найденные силы и моменты к соответствующим звеньям. Упростим схему нагружения, как описано выше и показано на рис. 11. Для этого вычислим
, Н·м; 3) кулисного камня I 3 = 0, M 3 = 0. Приложим найденные силы и моменты к соответствующим звеньям. Упростим схему нагружения, как описано выше и показано на рис. 11. Для этого вычислим 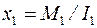 , м;
, м;  , м. Полученные смещения отложим в масштабе схемы на группе Ассура и на кривошипе. Заменим «старые» I 1, M 1 и I 2, M 2 «новыми» смещёнными I 1 и I 2 («старые» силовые факторы на рис. 12, а, б зачёркнуты крестиком).
, м. Полученные смещения отложим в масштабе схемы на группе Ассура и на кривошипе. Заменим «старые» I 1, M 1 и I 2, M 2 «новыми» смещёнными I 1 и I 2 («старые» силовые факторы на рис. 12, а, б зачёркнуты крестиком).
Картину нагружения дополним силами тяжести, найденными по формуле G = m·g, Н, силой полезного сопротивления  , направленной противоположно скорости
, направленной противоположно скорости  и реакциями внешних связей. Реакции неизвестны, поэтому показываем их пунктиром.
и реакциями внешних связей. Реакции неизвестны, поэтому показываем их пунктиром.
Составим уравнение моментов относительно точки В:
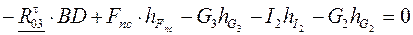 .
.
Из уравнения выведем и вычислим:  , Н.
, Н.
Предположим, что результат оказался положительным. Это будет означать, что направление реакции  выбрано правильно. При отрицательном результате первоначально выбранное направление
выбрано правильно. При отрицательном результате первоначально выбранное направление  меняем на обратное.
меняем на обратное.
Составим и решим графически уравнение равновесия кулисного камня 3:  . Для этого, выбрав предварительно масштабный коэффициент плана сил
. Для этого, выбрав предварительно масштабный коэффициент плана сил  Н/мм, построим цепочку векторов
Н/мм, построим цепочку векторов  и
и  (рис. 12, в).
(рис. 12, в).

Из начала этой цепочки проведём линию действия вектора  перпендикулярно DB, а из конца – линию действия вектора
перпендикулярно DB, а из конца – линию действия вектора  . Получим точку пересечения этих линий. В этой точке будет находиться начало первого и конец последнего вектора искомых реакций. Модули реакций вычислим по формуле:
. Получим точку пересечения этих линий. В этой точке будет находиться начало первого и конец последнего вектора искомых реакций. Модули реакций вычислим по формуле:
 , Н, (13)
, Н, (13)
где  – длина вектора на плане сил, мм.
– длина вектора на плане сил, мм.
Реакцию в шарнире В определим из уравнения равновесия кулисы 2:
 , где
, где  .
.
Графическое решение этого уравнения приведено на рис. 12, г. Как видно по рисунку, цепочку известных сил замыкает искомая реакция  . Её модуль вычислим по формуле (13). На этом реакции во всех кинематических парах группы Ассура определены.
. Её модуль вычислим по формуле (13). На этом реакции во всех кинематических парах группы Ассура определены.
Силовой расчёт начальной системы (табл.2, строка 6). Приложим в точке В (рис. 12, б) реакцию  и разложим момент МД на пару сил
и разложим момент МД на пару сил 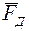 ,
,  с плечом lAB. Из уравнения моментов относительно точки А определим силу
с плечом lAB. Из уравнения моментов относительно точки А определим силу 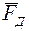 :
:
 ;
;
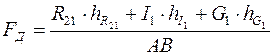 . Н.
. Н.
Искомый уравновешивающий (движущий) момент  , Н·м.
, Н·м.
 Реакцию в шарнире А определим графическим решением уравнения равновесия кривошипа:
Реакцию в шарнире А определим графическим решением уравнения равновесия кривошипа:  (рис. 12, д). Для этого, задавшись масштабным коэффициентом
(рис. 12, д). Для этого, задавшись масштабным коэффициентом  , Н/мм построим цепочку первых трёх векторов и замкнём её неизвестной реакцией
, Н/мм построим цепочку первых трёх векторов и замкнём её неизвестной реакцией  . Величину искомой реакции вычислим по формуле (13).
. Величину искомой реакции вычислим по формуле (13).
На этом силовой расчёт начальной системы закончен.
Для проверки силового расчёта определим МД с помощью «рычага Жуковского». Для этого построенный ранее план скоростей повернём на 90˚ (рис. 13). Перенесём параллельно самим себе все внешние силы и силы инерции со схемы механизма на повёрнутый план скоростей. Приложим силы к концам скоростей тех точек, к которым они были приложены на схеме. Силы, приложенные к неподвижным точкам, на план скоростей не переносим. Точки приложения сил инерции k1 и k2 находим по теореме подобия. Обозначим искомую движущую силу –  . Под действием приложенных сил «рычаг Жуковского» находится в равновесии. На этом основании составим уравнение моментов относительно полюса р:
. Под действием приложенных сил «рычаг Жуковского» находится в равновесии. На этом основании составим уравнение моментов относительно полюса р:
 .
.
Чтобы не перегружать рисунок, на нём показано плечо только одной силы  . Все плечи измеряются на рисунке в миллиметрах. Из полученного уравнения находим движущую силу:
. Все плечи измеряются на рисунке в миллиметрах. Из полученного уравнения находим движущую силу:
 , Н.
, Н.
Вычислим уравновешивающий (движущий) момент