Нелинейная динамика и синергетика

 

В нелинейных системах могут наблюдаться самые разнообразные процессы, принципиально отличающиеся от процессов в линейных системах. Одними из наиболее интересных процессов, которые в последнее время стали предметом углубленного изучения, являются процессы самоорганизации.

Процессы самоорганизации в нелинейных системах проявляются как уменьшение числа степеней свободы, эффективно описывающих систему. При этом в определенных случаях выделяются несколько степеней свободы, к которым подстраиваются все остальные. Они определяют динамику системы и поэтому часто называются параметрами порядка (порядок здесь понимается в смысле упорядочивания движения). Появление определенного порядка означает, что у системы в целом появляются свойства, которыми не обладает ни одна из подсистем. Принимая во внимание указанный эффект, соответствующую теорию самоорганизации в нелинейных системах называют синергетикой [15].

Термин синергетика ввел немецкий ученый Г. Хакен[16]. Он поясняет его следующим образом: "Я назвал новую дисциплину синергетикой. В ней исследуются совместное действие многих подсистем (преимущественно одинаковых или несколько различных видов), в результате которого на макроскопическом уровне возникает структура и соответствующее функционирование". В физических системах самоорганизация тесно связана с диссипативными [17] процессами (или, как их называют, диссипативными структурами движения). Сам термин "диссипативная структура" был введен бельгийским ученым И. Пригожиным. В работе[18] дается следующая характеристика этого эффекта: "... как удаленность от равновесия, так и нелинейность могут служить причиной возникновения упорядоченности в системе. Между упорядоченностью, устойчивостью и диссипацией (рассеиванием энергии ‑ Л. К.) возникает в высшей степени нетривиальная связь. Чтобы четче выделить эту связь, мы будем называть упорядоченные конфигурации, появляющиеся вне области устойчивости... диссипативными структурами (т. е. определенными конфигурациями диссипативных процессов в системе ‑ Л. К.)... Такие структуры могут существовать вдали от равновесия лишь за счет достаточно большого потока энергии и вещества... Диссипативные структуры являют собой поразительный пример, демонстрирующий способность неравновесности служить источником упорядоченности".

В закрытых равновесных физических системах диссипативные процессы устраняют любую упорядоченность ‑ устанавливается термодинамическое равновесие. В нелинейных открытых системах диссипация выступает в совершенно ином качестве. Ее совместное действие с другими процессами приводит к возникновению ярко выраженных структур движения, она влияет на их тип, форму, размеры[19].

Формы движения в нелинейных открытых системах по типу диссипативных структур имеют характерные особенности, среди которых необходимо указать следующие.

Установившееся движение здесь обычно является устойчивым, при этом различные начальные отклонения со временем выходят на один и тот же установившейся режим. Для линейных систем и целого класса нелинейных систем, например, для замкнутых физических систем установившейся режим характеризуется равновесным состоянием простой однородной структуры. Однако данная ситуация для многих открытых нелинейных систем является не правилом, а исключением. Здесь установившийся режим зачастую является более сложным. Его математическим образом является предельное множество, к которому притягиваются траектории в фазовом пространстве системы. Это предельное множество называют аттрактором.

Исследования показывают, что во многих случаях установившиеся режимы в нелинейных диссипативных системах обладают инвариантно-групповой структурой. Например, это могут быть фракталы ‑ структуры, подобные себе, на разных уровнях иерархии декомпозиции по принципу "целое‑части".

Наличие нескольких аттракторов дает новые возможности управления процессами в нелинейных диссипативных системах. Здесь в фазовом пространстве системы можно выделить границы, разделяющие области притяжения различных аттракторов. Малое изменение начальных данных вблизи этой границы может привести к качественно различному поведению на развитой стадии. Это свойство является общим для многих открытых нелинейных систем. В большинстве их них есть определенная область фазового пространства, где система особо чувствительна к внешним воздействиям (например, по типу резонансных явлений, динамического хаоса и др.). При этом амплитуда и продолжительность воздействий менее важны, чем их целевая направленность, согласованная с "готовностью" системы двигаться в соответствующем направлении. Эта "готовность" системы может быть создана искусственно, как один из способов управления нелинейными диссипативными системами. Подобный подход дает новые инструменты управления сложными нелинейными системами.

Вычислительное моделирование при исследовании диссипативных структур и явлений самоорганизации в нелинейных системах обладает характерными особенностями. Здесь необходимо органично сочетать аналитические методы исследования с вычислительными расчетами. Аналитические исследования позволяют произвести декомпозицию процессов в сложной нелинейной системе, выделить области притяжения, разделить быстрые и медленные движения, движения на аттракторах и др. В результате будет получена совокупность вычислительных моделей, позволяющая на основе вычислительных экспериментов, проводить анализ процессов со сложной структурой для исследуемых систем.

_______________________________________

 

Рассмотрим основные особенности процессов самоорганизации в нелинейных динамических системах в соответствии с работой А.А. Колесникова[20].

Сначала рассмотрим известный пример[21].

Пусть задана нелинейная динамическая система, поведение которой описывается уравнениями:

(1)

Для данной нелинейной системы при условии постоянная времени по координате будет относительно «малой», а сама координата системы (1) будет представлять «быстрые» движения, соответственно координата ‑ «медленные» движения. Асимптотически при 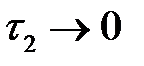система уравнений (1) будет иметь вид

(2)

Стационарные точки системы определяются из уравнений

(3)

На рис. 4.4.1 изображен фазовый портрет системы (1) при . Из рисунка видно, что траектории сначала устремляются к состоянию, которое представлено уравнением

, (4)

а затем движутся вдоль него к стационарным точкам, и , 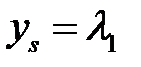. В теории самоорганизации рассмотренный процесс называется кооперативным процессом, а уравнение (4) – уравнением кооперативного состояния.

 

Рис. 4.4.1. Фазовый портрет системы (1) при

 

Таким образом, в системе (1) при возникают кооперативные процессы, основанные на приближении 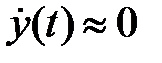и, следовательно, представлении ее движения на финишном этапе так называемым эволюционным уравнением

, (5)

записанным относительно «медленной» переменной . Этой переменной подчинена «быстрая» переменная в виде уравнения кооперативного состояния (4). В теории самоорганизации подобные «медленные» переменные представляют собой параметры порядка.

Необходимо отметить, что эволюционными уравнениями вида (5) описывается обширный класс систем (физических, химических, биологических и др.).

Согласно положениям теории самоорганизации в динамических системах, уравнение (5) имеет точку бифуркации – раздвоения решений при критическом значении . В этой точке в результате действий малых флюктуаций, обуславливающих хаотическое состояние системы (динамический хаос), движение системы разветвляется. При этом дальнейшее движение происходит по одной из двух возможных ветвей асимптотически устойчивого движения, т. е. может возникнуть спонтанная самоорганизация. Описанное явление называется бифуркацией типа «вилка».

Явление бифуркации решений для системы (1) зависит от соотношения параметров , . На рис. 4.4.2 изображен фазовый портрет системы (1) при . Из рисунка видно, что траектории здесь сразу устремляются к стационарным точкам , , а кооперативные процессы заметно ослабляются.

Рис. 4.4.2. Фазовый портрет системы (1) при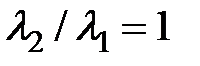

 

Явление спонтанной самоорганизации в динамических системах может быть рассмотрено в общем случае.

Пусть поведение объекта описывается системой дифференциальных уравнений, для которого состояния можно разделить на две части: «медленные» и «быстрые» . Тогда движение объекта может быть описано в виде двух дифференциальных уравнений:

(6)

Далее предполагается, что существует некоторое инвариантное множество

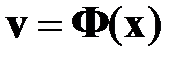(7)

такое, что на нем удовлетворятся второе уравнение системы (6), т. е.

.

При указанных условиях исходная система (6) дифференциальных уравнений становится эквивалентной дифференциальному уравнению

. (8)

Уравнение (8) – это эволюционное уравнение, а – параметр порядка. Для возникновения указанной ситуации на асимптотическом этапе движения исходной системы необходимо, чтобы многообразие (7) было притягивающим, т.е. асимптотически устойчивым. Такое асимптотически устойчивое инвариантное многообразие, содержащие аттрактор исходной системы, называется инерциальным многообразием[22]. Обратим внимание на то, что движение динамической системы на аттракторе (8) обычно значительно проще по сравнению с общим случаем (6). Этот эффект объясняется тем, что при наличии инерциального многообразия можно опустить переходной процесс и рассматривать движение системы только на указанном многообразии. В этом случае переменные, входящие в исходную систему, можно разделить на две группы: «существенные» – , определяющие динамику, и «несущественные» – , которые подчиняются первым и следуют за ними.

Применительно к объекту, который описывается системой (1), соотношение (4) является инвариантным многообразием типа (7), а х (t) – параметром порядка. Движение на указанном многообразии описывается эволюционным уравнением (5) типа (8).

Как указывается в работе А. А. Колесникова[23], «параметры порядка в синергетике формируют макроскопическую структуру нелинейной системы. При этом поведение любой из координат … системы однозначно определяется параметрами порядка. Это означает, что движение системы в ее фазовом пространстве управляется параметрами порядка и подчинено именно им. В этом и состоит принцип подчинения в синергетике. Суть подчинения состоит в том, что поведение системы определяется иерархией масштабов времени между «ускоренными» процессами изменения некоторых переменных и «медленными» процессами эволюции параметров порядка. Обычно число параметров порядка существенно меньше числа координат системы, т. е. в результате перехода к параметрам порядка существенно сокращается число степеней свободы системы, что приводит к значительному сжатию информации. Однако оказывается, что отдельные координаты …, объединяясь в кооперативное движение, в свою очередь, оказывают воздействие на сами параметры порядка. Это означает, что параметры порядка, с одной стороны, формируют движение отдельных координат системы, а с другой стороны, отдельные координаты в совокупности порождают параметры порядка. В синергетике описанное явление называют круговой причинностью. Объединяясь в параметры порядка, отдельные координаты системы стремятся найти консенсус[24]. Иначе говоря, подчинение и поиск согласия являются двумя базовыми свойствами синергетического подхода».

Следует также отметить, что механизмы формирования параметров порядка во многом опираются на приближенный метод «малого» параметра в теории нелинейных дифференциальных уравнений, которому посвящена обширная литература.

Для того чтобы показать возможность направленной самоорганизации в системе (1) со свойствами, определяемыми эволюционным уравнением (3), в работе[25] вводится в рассмотрение обратная связь :

(12)

Далее, вводится следующая макропеременная:

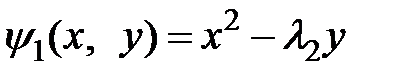. (9)

Функция (9) на финишных этапах движения системы (1) должна быть согласно (4) равной нулю. Для того чтобы удовлетворить условию после выхода системы (1) на финишный этап движения, вводится простейшее функциональное уравнение

.

Тогда на основе подстановки сюда функции (9) с учетом исходных уравнений (1) находится u ₁ – обратная связь:

.

Далее на основе подстановки u ₁ в (1) находятся уравнения сконструированной системы:

(10)

Система (10) имеет состояние как притягивающее многообразие – аттрактор. Для того чтобы это показать, находится из первого и второго уравнений (10) величина dt и подставляется в систему (10) в следующей симметричной форме:

.

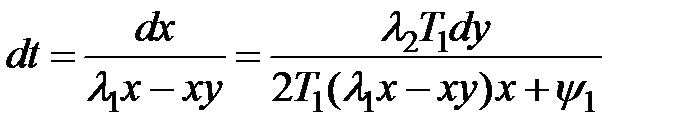Положив функцию , после интегрирования находится частный интеграл , который совпадает с выражением 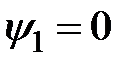(9). Это означает, что система (10) имеет асимптотический аттрактор .

Система (10), стартуя из произвольных начальных условий x ₀, 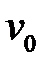и, следовательно, , неизбежно через время 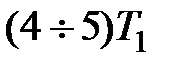должна выйти на аттрактор 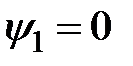– притягивающее многообразие. Другими словами, ее движение на финишном этапе будет обязательно протекать по многообразию (9) или в его окрестности. Это движение описывается уравнением

. (11)

Дифференциальное уравнение (11) описывает движение системы (10) на аттракторе , т. е. на ее финишном этапе.

На рис. 4.4.3 изображен фазовый портрет системы (10) при и 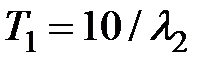, из которого видно, что траектории сначала устремляются к аттрактору (9), а затем движутся вдоль него к стационарным точкам 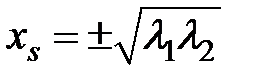, , т. е. имеет место кооперативный процесс. Аналогично на рис. 4.4.4 изображен фазовый портрет системы (10) при и .

Рис. 4.4.3. Фазовый портрет системы (10) пр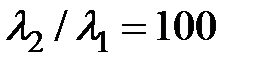и и

 

Рис. 4.4.4. Фазовый портрет системы (10) при и

 

Из приведенного рисунка следует, что в отличие от случая (рис. 4.4.2), траектории сближаются с аттрактором (9), а затем движутся вдоль него к стационарным точкам , , т. е. по-прежнему возникают кооперативные явления. Система (1) в установившемся режиме может равновероятно находиться в одном из двух возможных состояний: . В системе (10) также устанавливаются эти состояния, при этом функция . В целом это означает полную идентичность поведения систем (1) и (10) на этапе самоорганизации».

Итак, в системе может быть направлено сформирована желаемая структура – аттрактор, на которой возникает процесс самоорганизации. Такое явление называется целенаправленной самоорганизацией. Отмечается также, что в системе

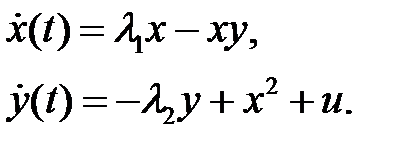(12)

за счет выбора соответствующих обратных связей можно обеспечить и другие виды бифуркации, т. е. иные типы самоорганизации.

В синергетике, помимо описанной выше бифуркации типа «вилка», распространена также транскритическая бифуркация[26], уравнение которой относительно параметра порядка имеет вид:

. (13)

и представляет собой широко известное в экологии логистическое уравнение, которое, в свою очередь, является частным случаем уравнения Бернулли.

Транскритическая бифуркация невозможна в системе (12) при любом сочетании параметров , в случае 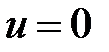. Однако, за счет выбора соответствующей функции , указанную бифуркацию можно обеспечить. С этой целью в работе[27] вводится макропеременная

,

подставив которую в уравнение

,

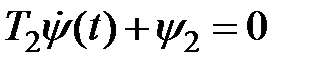можно получить с учетом уравнений (1) следующую обратную связь:

.

Подставив , т. е. , в первое уравнение системы (1), можно получить уравнение

,

которое описывает движение замкнутой системы на многообразии и точно совпадает с (13). Это означает, что в системе (1) с обратной связью на финишном этапе через время возникнет движение на аттракторе уже с транскритической бифуркацией (13). На рис. 4.4.5 изображен фазовый портрет системы с обратной связью , из которого видно, что траектории сначала устремляются к аттрактору , а затем движутся вдоль него к стационарной точке , , т. е. возникает кооперативный процесс с транскритической бифуркацией.

 

Рис. 4.4.5. Фазовый портрет системы с обратной связью u ₂

 

Если ввести макропеременную

и подставить ее в функциональное уравнение

,

то тогда в силу исходных уравнений (1) может быть найдена следующая обратная связь:

.

Подставив теперь эту обратную связь в (12), можно получить уравнения замкнутой системы:

(14)

Полученная система (14) имеет притягивающее инвариантное многообразие , к которому устремляются все ее фазовые траектории. Движение системы (14) вдоль этого многообразия описывается дифференциальным уравнением

.

Из этого уравнения и получается эволюционное уравнение вида (13) с транскритической бифуркацией, а при из него следует уравнение вида

.

Это типичное эволюционное уравнение синергетики с бифуркацией типа «седло–узел», часто встречающейся в различных физических приложениях.

Таким образом, в работе[28] показано, что «введение в систему (12), изначально используемую в работах Г. Хакена для демонстрации идеи самоорганизации в синергетике, соответствующих обратных связей позволяет сформировать желаемые типы бифуркаций и тем самым реализовать направленную самоорганизацию системы».

_________________________________

 

Опираясь на идеи синергетики, в настоящее время активно разрабатывается синергетическая теория управления (СТУ). СТУ – это новое направление в общей теории управления. отражающее идеологию единства процессов самоорганизации и управления. При этом в дополнение к классической теории автоматического регулирования и теории оптимального управления в качестве цели конструирования систем, ставится не только выполнение требований к характеру переходного процесса, а также обеспечение желаемого асимптотического поведения системы на аттракторе или в его близкой окрестности.

Для сложных динамических систем процессы самоорганизации носят многоуровневый характер. Так в соответствии с работой[29] «…в СТУ целью синтезируемой системы является достижение соответствующего желаемого аттрактора, размерность которого обычно существенно меньше размерности исходного пространства состояний системы. Отсюда вытекает идеология процессов обработки информации и управления в сложных нелинейных динамических системах: для этого необходимо, чтобы указанные процессы включали в себя, по меньшей мере, две фазы: во-первых, фазу расширения и, во-вторых, фазу сжатия пространства состояний. Эти фазы реализуются с помощью соответствующей совокупности обратных связей. При этом в фазе расширения в системе формируется подмножество различных альтернатив поведения для ее взаимодействия с внешней средой или другими системами. В фазе сжатия система преобразует область притяжения аттракторов, ранее построенных, в один из желаемых аттракторов – цель системы».

Создание синергетической теории управления является одной из актуальных проблем современной науки об управлении.

В целом синергетическая теория показывает, что возможности управления для сложных нелинейных объектов являются ограниченными. Дело в том, что траектории движения сложных нелинейных объектов в фазовом пространстве представляют собой как участки упорядоченного движения, так и участки хаотичного движения ‑ динамического хаоса. В общем случае упорядоченное движение возникает из хаоса и при дальнейшем движении приходит в хаос. Управление на упорядоченных участках может быть эффективно организовано, но оно имеет ограниченный горизонт, определяемый возможностями прогнозирования движения объекта. Однако и на участках хаотического движения можно в определенной степени организовать целенаправленное движение объекта. На участках динамического хаоса движение может переключаться в различных направлениях. Поэтому целенаправленным воздействием на хаотическое движение можно упорядочить его в желательном направлении. При этом с целью переключения траектории движения объекта в желаемом направлении создание хаоса может быть целенаправленным управленческим приемом.

 

[1] Казаринов, Л.С. Прогнозирование случайных колебательных процессов на основе метода экспоненциального сглаживания / Л.С. Казаринов, С.И. Горелик // Автоматика и телемеханика, РАН. – 1994. – №10. – С. 27–34.

Казаринов, Л.С. Оценка положения и скорости летательного аппарата на основе метода экспоненциального сглаживания результатов траекторных измерений / Л.С. Казаринов, С.И. Горелик // Известия РАН. Техническая кибернетика. – 1994. – №6. – С. 83 – 94.

Казаринов, Л.С. Построение наблюдений состояния динамических систем на основе аппроксимирующих фильтров / Л.С. Казаринов, А.Е. Гудилин // Программное обеспечение. Микропроцессорная техника сложных автоматических систем и их устройства: сб. науч. тр. – Челябинск: ЧГТУ, 1995. – С. 46 – 49.

[2] Калман, Р.Е. Новые результаты в теории фильтрации и теории предсказывания / Р.Е. Калман, Р.С. Бьюси // Тр. Амер. Общ-ва инж.-мех. Серия «Техническая механика». – 1961. – С. 95 ‑ 107.

[3] Шмидт, Дж. Линейные и нелинейные методы фильтрации / Дж. Шмидт // Фильтрация и стохастическое управление в динамических системах / под ред. К.Т. Леондеса. ‑ М.: Мир, 1980. – С. 49‑73.

Пер. с англ. CONTROL AND DYNAMIC SYSTEMS: Advances in Theory and Applications / ed. C.T. Leondes. – New York, San Francisco and London: Academic Press. – 1976.

[4] Гельфанд, И.М. Вариационное исчисление / И.М. Гельфанд, С.В. Фомин – М.: Физматгиз, 1961.

[5] Понтрягин, Л.С. Математическая теория оптимальных процессов / Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, В.Ф. Мищенко. – М.: Физматгиз, 1961.

[6] Беллман, Р. Динамическое программирование / Р. Беллман. – М.: ИЛ, 1960.

[7] Деруссо, П. Пространство состояний в теории управления (для инженеров) / П. Деруссо, Р. Рой, Ч. Клоуз ‑ М.: Наука, 1970.‑ С. 572‑573.

[8] Калман, Р. Очерки по математической теории систем / Р. Калман, П. Фалб, М. Арбиб. – М.: Мир, 1971.

[9] Там же, стр. 76‑77.

[10] Калман, Р.Е. Когда линейная система является оптимальной? / Р.Е. Калман // Тр. амер. общ-ва инж.-мех. Серия Д, №1: Мир, 1964. – С. 69‑84.

[11] Александров, А.Г. Синтез регуляторов многомерных систем / А.Г. Александров. – М.: Машиностроение, 1986. – 272 с.

[12] Месарович М. Общая теория систем: математические основы / М. Месарович, Я. Такахара. – М.: Мир, 1978. – С. 297–301.

[13] Лат. conventio ‑ условное соглашение.

[14] Qin, S.J. A survey of industrial model predictive control technology / S.J.Qin, T.A. Badgwell // Control Engineering Practice. –2003. –11. – P. 733‑764.

[15] Греч. σύν ‑ совместно, ’έργον ‑ действие.

[16] Хакен, Г. Синергетика / Г. Хакен. ‑ М.: Мир, 1980. ‑ 404 с.

[17] Лат. dissipatio ‑ рассеяние (здесь ‑ рассеяние энергии).

[18] Николис, Г. Самоорганизация в неравновесных системах / Г. Николис, И. Пригожин. ‑ М.: Мир, 1979. ‑ 512 с.

[19] Интересно отметить, что в глобальном плане стремление закрытых физических систем к термодинамическому равновесию служит обоснованием концепции роста энтропии и "тепловой смерти" Вселенной, как конечного этапа ее развития. Напротив, теория самоорганизации открытых физических систем служит основой концепции последовательной структуризации процессов при развитии Вселенной.

[20] Колесников, А.А. Синергетические методы управления сложными системами: Теория системного синтеза / А.А. Колесников. – М.: КомКнига, 2006. – 240 с.

Колесников Анатолий Аркадьевич, заслуженный деятель науки и техники РФ, доктор технических наук, профессор, заведующий кафедрой синергетики и процессов управления Таганрогского государственного радиотехнического университета. Труды по синергетической теории управления.

[21] Хакен Г. Информация и самоорганизация. Макроскопический подход к сложным системам / Г. Хакен. – М.: Мир, 1991; изд. 2.– М.: КомКнига, 2005.

[22] Компьютеры и нелинейные явления: Информатика и современное естествознание / под ред. А.А. Самарского. – М.: Наука, 1988.

[23] Колесников, А.А. Синергетические методы управления сложными системами: Теория системного синтеза / А.А. Колесников. – М.: КомКнига, 2006. – 240 с.

[24] Пригожин, И. От существующего к возникающему / И. Пригожин. – М.: Наука, 1985; изд. 3.– М.: КомКнига, 2006.

[25] Колесников, А.А. Синергетические методы управления сложными системами: Теория системного синтеза / А.А. Колесников. – М.: КомКнига, 2006. – С. 97–98.

[26] Хакен, Г. Информация и самоорганизация. Макроскопический подход к сложным системам / Г. Хакен. – М.: Мир, 1991; изд. 2. – М.: КомКнига, 2005.

Николис Г. Познание сложного /Г. Николис, И. Пригожин. – М.: Мир, 1990; изд. 2. – М.: УРСС, 2003.

Компьютеры и нелинейная являения: Информатика и современное естествознание / под ред. А.А. Самарского. – М.: Наука, 1988.

[27] Колесников, А.А. Синергетические методы управления сложными системами: Теория системного синтеза / А.А. Колесников. – М.: КомКнига, 2006. – С. 100–101.

[28] Там же.

[29] Там же, стр. 102–107.