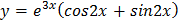I. Дифференциальные уравнения с разделяющимися переменными.
Опр. Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если его можно представить в виде
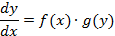
Проинтегрируем почленно это уравнение и получим общее решение: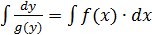 
Алгоритм решения:
1. Разделить переменные
2. Найти общее решение уравнения интегрируя его почленно
3. Найти частное решение по начальным данным (если они есть)
4. Сделать проверку
Замечание. Часто уравнение с разделяющимися переменными называют уравнение вида:
Умножают обе части уравнения на дробь 
и получают уравнение вида
Затем интегрируют это равенство и находят общее решение
II. Линейные дифференциальные уравнения 1-го порядка
Опр. Уравнение вида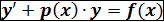 
называется линейным дифференциальным уравнением 1-го порядка. В этом уравнении искомая функция y и её производная 
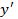входят 1-ой степени (линейно)
· Если f(x)≠0, то уравнение называется неоднородным
· Если f(x)=0, то уравнение называется однородным
Один из способов решения линейного дифференциального уравнения 1-го порядка – это метод подстановки Бернулли.
1) По методу Бернулли решение уравнения ищется в виде
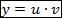(1)
где u=u(x), v=v(x) - некоторыедифференцируемые функции. Одну из этих функций можно взять произвольно, другая определяется из уравнения
2) Найдем производную:
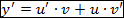(2)
3) Подставим равенства (1) и (2) в уравнение 
и получим:
(*)
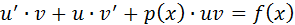Группируем слагаемые
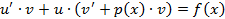
Так как одну из функций можно взять произвольно, то будем считать, что функция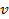 
такая, что
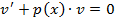
Это дифференциальное уравнение с разделяющимися переменными:
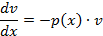
Умножим его на на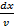 
и получим:
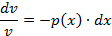
4) Находим интегралы, а значит и функцию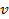
5) Подставляем функцию 
в уравнение (*) и находим 
6) Обе функции подставляем в уравнение (1) и получаем решение дифференциального уравнения
III. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Опр. Уравнение вида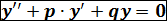 
(1) называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами p и q. (Искомая функция 
, 
, 
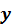входят в него линейно)
Общее решение уравнения (1) зависит от корней характеристического уравнения:
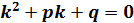(2),
которое получается из уравнения (1) заменой 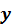, , на соответствующие степени k, причем сама функция y заменяется 1.
Возможны три случая:
| Корни уравнения (2) | Общее решение уравнения | Частные решения уравнения |
Действительные и различные (D>0)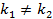 
| 
| 
|
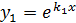
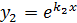
Действительные и равные (D=0) 
| 
| 
|
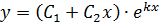
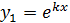
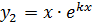
Комплексно сопряженные (D<0)
| 
| 
|
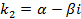
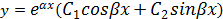
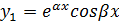
Решения типовых примеров
Пример 1. Найти общее и частное решение уравнения 
, если
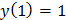
Решение:
Это дифференциальное уравнение с разделяющимися переменными. Умножим его на дробь
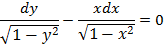
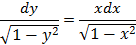
Интегрируя это равенство, найдем общее решение дифференциального уравнения
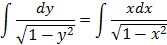
Левая часть – это табличный интеграл
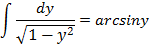
Правая часть уравнения – это интеграл, который найдем способом подстановки:
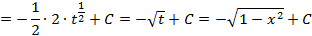
Итак, общее решение дифференциального уравнения имеет вид:
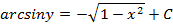
Так как 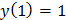, то подставим х=1 и у=1 в общее решение уравнения и получим:
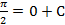или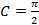 
Значит частное решение дифференциального уравнения имеет вид:
Пример 2. Найти общее решение уравнения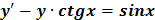 
Решение:
Это линейное дифференциальное уравнение 1-го порядка. Решим его с помощью подстановки Бернулли
1) По методу Бернулли решение уравнения ищется в виде
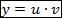(1)
где u=u(x), v=v(x) - некоторыедифференцируемые функции. Одну из этих функций можно взять произвольно, другая определяется из уравнения
2) Найдем производную:
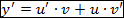(2)
Подставим равенства (1) и (2) в заданное в условии уравнение 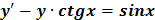и получим:
(*)
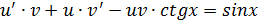Группируем слагаемые
Так как одну из функций можно взять произвольно, то будем считать, что функция 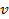такая, что
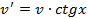
Это дифференциальное уравнение с разделяющимися переменными:
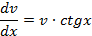
Умножим его на на 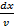и получим:
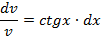
Левая часть уравнения– это табличный интеграл
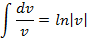
Правая часть уравнения – это интеграл, который найдем способом подстановки:
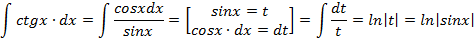
Значит решение этого дифференциального уравнения имеет вид:
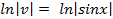
Подставим найденное решение в уравнение (*) и найдем функцию u
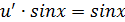
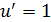
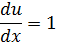
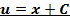
Обе функции подставляем в уравнение (1) и получаем решение дифференциального уравнения
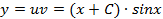
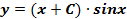
Пример 3. Найти общее и частное решение уравнения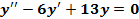 
, если y=1 и 
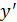=5 при х=0
Решение:
Решим соответствующее характеристическое уравнение:
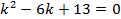
D=36-52=-16<0
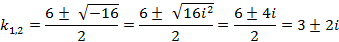
Общее решение уравнения: 
Найдем y’ как производную произведения:
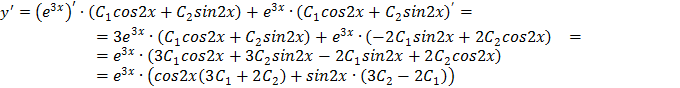
Т. к. х=0, у=1, 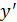=5, то получим систему:
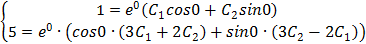
e0=1, Sin0=0, Cos0=1, значит система упроститься и примет вид:
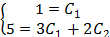
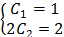
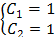
Частное решение уравнения: 
