а) Через точку А можно провести только одну перпендикулярную прямую АH к прямой BT; остальные прямые, проходящие через точку А и пересекающие BT, называются наклонными (прямые АB, AC и АT).
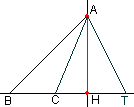
б) Длина перпендикуляра (длина отрезка А H), проведенного из точки А на прямую BT,— это самое короткое расстояние от A до BT.
Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
с) Несколько перпендикуляров, проведенных через различные точки к одной прямой, никогда между собой не пересекаются.
15. Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки— сторонами треугольника.
Вершины: А, В, С
Стороны: АС, АВ, ВС, или соответственно b, c, а.
Периметром треугольника, как в прочем и любой фигуры, называется сумма длин всех сторон. Периметр - греч.слово peri – «вокруг», «около» и metreo – «измеряю».
16. Если два треугольника равны, то элементы (т.е.три стороны и три угла) одного треугольника соответственно равны элементам другого треугольника.
У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)
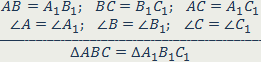
В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.
17. Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы. Теорема состоит из двух утверждений: утверджение-условие, утверждение-вывод. Теорему всегда можно записать в виде:
Если «утверджение-условие», то «утверждение-вывод».
Признак – это свойство, по которому познают или узнают предмет, свойство объекта, обуславливающее его различие или общность с другими объектами.
Признак в математике это теорема, в которой утверждается, что определенные условия обеспечивают принадлежность фигуры (фигур) конкретному множеству, которое было определено ранее (например, множеству треугольников).
18. Теорема. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если
то 
19. Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
ha –высота, проведенная из вершины А к стороне а,
hb - высота, проведенная из вершины В к стороне b,
hc - высота, проведенная из вершины С к стороне с.
20. Медианой (лат. mediāna — средний) треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке.
21. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
la –биссектриса угла А, lb - биссектриса угла B,
lc - биссектриса угла С.
Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.
22. Свойства медианы, биссектрисы и высоты треугольника. В любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке.
23. Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
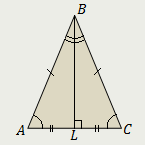Если АВ = ВС, то треугольник АВС – равнобедренный.
