Расчетно-графическая работа К5
Сложное движение точки при переносном вращательном движении.
Дано: Диск радиуса R = 72 см вращается вокруг неподвижной оси O z, перпендикулярной плоскости диска (x O y) (рис.5.1) и проходит через точку O (диск вращается в своей плоскости).
Уравнение вращательного движения диска дано:
, 
, 
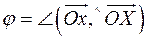, где 
.
Положительное направление отсчета угла 
показано на рис.5.1 дуговой стрелкой, направленной против часовой стрелки.
По ободу диска движется точка М, траекторная координата этого движения, отсчитываемая от точки «Н», изменяется согласно уравнению
= 
+ A О sin k t, где , A О, k – постоянные величины: =0 см;
A О = 36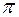 
см, k= 
. ОО1 = L = 
см.
Определить абсолютную скорость и абсолютное ускорение (относительно неподвижной системы координат 
) точки М в момент времени 
, где 
.
Решение:
За подвижную систему отсчета принимаем диск, а связанные с ним оси координат ─ подвижные оси (изображены на рис 5.2).
За абсолютную (неподвижную) систему отсчета принимаем подшипник O, а связанные с ним оси координат XOYZ ─ неподвижные оси).
─ Относительное движение − перемещение точки М относительно диска в подвижной системе координат по ободу диска, т.е. по окружности (траекторный или естественный способ задания движения точки); все кинематические характеристики этого движения обозначаются с индексом «r»: 
, 
, 
.
─ Переносное движение − движение неизменяемой среды, неизменно связанной с подвижной системой отсчета Псо - (диском), относительно неподвижной системы отсчета XOYZ − (вращательное вокруг оси OZ); все кинематические характеристики этого движения обозначаются с индексом «
»: 
, 
, 
,, 
, 
.
─ Абсолютное движение −перемещение точки М относительно неподвижной системы отсчета XOYZ; все кинематические характеристики этого движения обозначаются с индексом «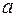
»: 
, 
.
На рис.5.2 изображено положение диска и связанной с ним под-
вижной системы координат в заданный момент времени :
= (1/3)·1³ = 1/3 рад = 19°
Кинематические характеристики точки М в относительном
Движении
Для этого следует воспользоваться формулами раздела “ Кинематика точки” ¾ при естественном (траекторном) способе задания ее движения.
Траекторная координата точки М, заданная уравнением
= + A О sin k t,
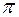после подстановки – =0 см; A О = 36 см, k= , примет вид
= 36π· sin (π/6) ·t. (5.1)
При t=1с: 
= 36·3,14· sin (π/6) 1=56,55 см.
a = 
= 56,55 / 72 = 0,785 рад = 45°; β = a − 
.
На рис.5.2 определено положение точки М на диске в момент времени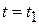 
(а не в произвольном положении, показанном на рис.5.1) в подвижной (относительной) системе отсчета ¾ при естественном (траекторном) способе задания ее движения, при котором >O.
Cкорость точки М: 
, где 
─ орт касательной в данной точке траектории, направленный в сторону возрастания траекторной координаты s;
= 
(5.2)
= 6 π2 0,866 = 59,2 × 0,866 = 52,3 см/с; так как > 0, то .
Ускорение точки М: 
, (5.3)
где 
─ касательное, а 
─ нормальное ускорения точки; 
= 
; (5.4)
= - p3 0,5= - 15,5 см/с2. Так как < 0, то 
¯ .
= 
; 
= 51,32/ 72 = 36,5 см/с2, (5.5)
где ρ ─ радиус кривизны траектории в данной точке.
Все векторы , 
и 
определены для момента времени 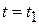и изображены на чертеже (без определения 
).
Кинематические характеристики точки М в переносном
Вращательном движении
Для этого следует воспользоваться формулами раздела “ Кинематика твердого тела” для случая вращательного движения твердого тела (диска), принятого за подвижную систему отсчета () вокруг оси O Z.
, 
, 
, 
, 
, 
.
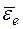Угловая скорость диска: 
= 
с-1. (5.6)
= 1 с-1; так как >0, то OZ.
Угловое ускорение диска: 
= 
с-2 . (5.7)
= 2 с-2; так как > 0, то .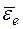
Скорость точки в переносном вращательном движении:
; величина скорости 
, (5.8)
где 
– расстояние точки М до оси вращения тела, принятого за подвижную систему отсчета; в данном случае = МО = 
, где 
, 
─ координаты точки М, как видно из рис.6.9 определяются следующим образом:
; 
. (5.9)
= 72 0,899 – 50,76 0,946 =
= 64,7 – 48 = 16,7 см;
= 72 0,438 + 50,76 0,325 =
= 31,5 + 16,5 = 48 см.
= 
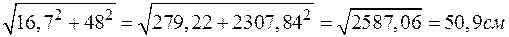
Скорость точки М в переносном движении:
; 
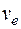
=1 50,9 = 50,9 см/с, вектор 
в сторону .
Ускорение точки в переносном движении 
= + , (5.10)
где осестремительное ускорение точки в переносном движении,
= 
, величина его ─ 
= 
; (5.11)
= 50,9 см/с2.
Направление вектора ─ по МО от точки М к оси вращения ОZ.
Вращательное ускорение точки М в переносном движении,
= 
, величина его ─ 
= 
; (5.12)
= 2 50,9 = 101,8 см/с2.
Так как вращение диска происходит вокруг оси ОZ ускоренно, т.е.
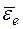
, то и вектор 
.
Все векторы определены для данного момента времени 
и направление их показано на рис.5.2 (без определения геометрической суммы ускорений ─ ).
Определение ускорения Кориолиса
Ускорение Кориолиса определяется векторным произведением
(5. 13),
из которого следуют его величина и направление.
Согласно правилу векторного умножения, вектор 
направлен перпендикулярно плоскости, в которой лежат векторы 
и 
(рис. 5. 2), в ту сторону, откуда поворот от к на наименьший угол кажется против направления часовой стрелки ( Oz; , т.е. ¯ 
).
Величина ускорения Кориолиса определяется как
. (5. 14)
= 2×1×51,3× sin 90° = 102,6 см/с2.
3. Кинематические характеристики точки в абсолютном движении
Для определения скорости и ускорения точки М в абсолютном движении, необходимо воспользоваться теоремами «о сложении скоростей и сложении ускорений», где 
, 
─ являются результатом геометрического суммирования соответствующих величин относительного и переносного движения:
, величина скорости: 
. (5.15)
или в проекциях на оси неподвижной системы координат OXYZ:
, величина: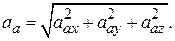 
(5.16)
Как видно из рис.5.2 векторы всех составляющих скоростей и ускорений точки М лежат в плоскости XOYZ, в которой лежат и оси М , поэтому в данном примере рациональнее найти величины 
и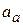 
из следующих выражений:
,
где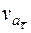 
= 
см/с;
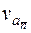
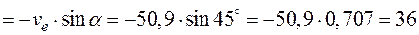см/с.
= 
см/с.
, где
= 
= 
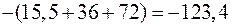см/с2;
= 
= 
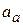
см/с2.
см/с2
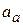
Ответ: = 39 cм/c; = 160 cм/c²
