3.4.1. Каким уравнением описывается устойчивое инерционное звено
первого порядка с выходом y(t) и входом x(t)?
Ответ: 2
3.4.2. Каким уравнением описывается идеальное интегрирующее звено с
входом x(t) и выходом y(t)?
Ответ: 3
3.4.3. Каким уравнением описывается вход-выходная связь f: x → y у консервативного звена?
Ответ: 2
3.4.4. Каким уравнением описывается идеальное дифференцирующее
звено, имеющее вход x и выход y?
Ответ: 5
3.4.5. Какой передаточной функцией описывается форсирующее звено
первого порядка?
Ответ: 3
3.4.6. Какому типовому звену соответствует передаточная функция
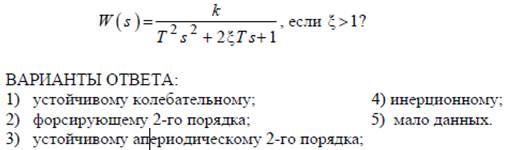
Ответ: 3
3.4.12. Каким аналитическим выражением описывается весовая функция
устойчивого звена с передаточной функцией
Ответ: 3
3.4.13. Каким аналитическим выражением описывается переходная функ-
ция идеального интегрирующего звена?
Ответ: 1
3.4.16. Каков вид графика переходной функции у звена с передаточной
Функцией
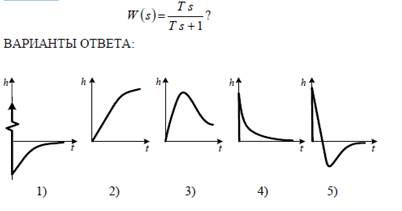
Ответ: 4
3.4.18. Какой график переходной функции соответствует звену, описы-
ваемому дифференциальным уравнением
Ответ: 5
3.4.19. Какой график весовой функции соответствует звену, описы-
ваемому дифференциальным уравнением
Ответ: 2
3.4.20. Определите вид графика переходной функции системы с пере-
даточной функцией
Ответ: 5
3.4.24. Каков вид графика амплитудно-частотной характеристики устой-
чивого апериодического звена первого порядка?
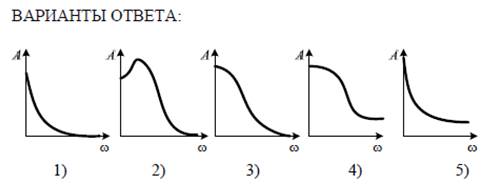
Ответ: 3
3.4.27. Определите вид графика фазовой частотной характеристики консер-
вативного звена.
Ответ: 2
3.4.29. Определите предельное значение фазовой частотной характеристики
при ω → ∞ у соединения звеньев с приведенными на рис. 3.39 переходными функциями.
Ответ: 3
3.4.30. Какой амплитудно-фазовый годограф соответствует устойчивому
инерционному звену первого порядка?
Ответ: 2
3.4.32. Какой амплитудно-фазовый годограф соответствует звену с пере-
даточной функцией
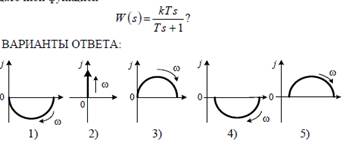
Ответ: 3
3.4.34. Какой амплитудно-фазовый годограф соответствует устойчивому
колебательному звену второго порядка?
Ответ: 1
3.4.40. Какой график аппроксимированной ЛАЧХ соответствует форси-
рующему звену с передаточной функцией W(s)= k (T s + 1)?
Ответ: 4
3.4.42. Какой график логарифмической фазовой частотной характеристики
соответствует устойчивому инерционному звену первого порядка?
Ответ: 4
4.2.1. Определите передаточную функцию Wx g (s)системы, операторно-структурная схема которой представлена на рис. 4.1.
Ответ: 2
4.2.2. Определите передаточную функцию Wx f (s) системы, опера-
торно-структурная схема которой представлена на рис. 4.2.
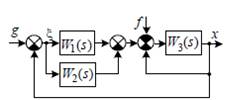
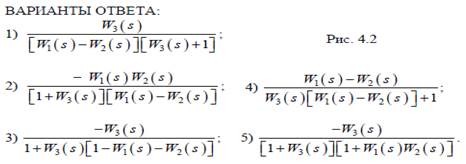
Ответ: 3
4.2.3. Определите передаточную функцию Wy x (s) системы, опера-
торно-структурная схема которой представлена на рис. 4.3.
4.2.4. Определите передаточную функцию Wy x (s) системы, опера-
торно-структурная схема которой представлена на рис. 4.4.
Ответ: 1
4.2.5. Определите передаточную функцию W ξ g (s) системы, операторно-структурная схема которой представлена на рис. 4.5.
Ответ: 1
4.2.6. Определите передаточную функцию W ξ x (s) системы, операторно-структурная схема которой представлена на рис. 4.6.
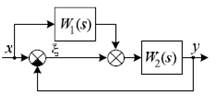
Ответ: 5
4.2.7. Определите передаточную функцию W ξ f (s)системы, операторно-структурная схема которой представлена на рис. 4.7.
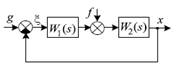
Ответ: 3
4.2.8. Определите передаточную функцию W ξ f (s)системы, опера-
торно-структурная схема которой представлена на рис. 4.8.
Ответ: 5
4.2.11. Определите передаточную функцию Wy x (s)системы, операторно-структурная схема которой приведена на рис. 4.11.
Ответы: 3
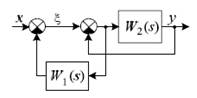
4.2.12. Определите лапласово изображение сигнала y (t)в приведенной
на рис. 4.12 системе при условии,что x (t)=2 t + 3⋅1(t).
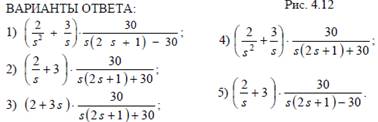Ответы:4
4.2.13. Определите лапласово изображение сигнала ξ (t)в приведенной на рис. 4.13 системе при x (t)= t 2.
Ответ: 2
