1. Функция. Определение, область существования, способы задания, классификация функций.
2. Предел функции непрерывного аргумента. Односторонние пределы. Предел функции при неограниченном
возрастании Х, геометрическая иллюстрация.
3. Числовая последовательность. Предел числовой последовательности.
4. Предел функции в точке, геометрическая иллюстрация
5. Бесконечно малые величины, их основные свойства. Ограниченные функции. Бесконечно большие функции и их связь с бесконечно малыми.
6. Основные теоремы о пределах. (Теорема о связи функции с её пределом, о пределе суммы, частного, произведения доказать самостоятельн.)
7. Признаки существования предела функции. 1 и 2 замечательные пределы (изучить самостоятельно).
- Непрерывность функции в точке и на интервале. Свойства непрерывных в точке функций.
- Точки разрыва функций и их классификация. Привести примеры.
- Свойства, непрерывных на отрезке функций. Теоремы Вейерштрасса, Больцано – Коши.
- Сравнения бесконечно малых величин. Эквивалентные бесконечно малые. Приложение эквивалентных бесконечно малых для вычисления пределов. Основные эквивалентные величины.
- Производная функции. Геометрический смысл, уравнения касательной и нормали. Механический смысл производной (изучить самостоятельно).
- Дифференцируемость функции в точке и на интервале. Связь между дифференцируемостью и непрерывностью функции.
- Производная суммы, произведения, частного дифференцируемых функций. Сложная функция и её дифференцирование. (Вывести самостоятельно).
- Производная степенной, логарифмической функций (вывод самостоятельно).
- Производная основных элементарных функций (вывод самостоятельно).
- Обратные функции, их свойства и дифференцирование.
- Обратные тригонометрические функции и их дифференцирование (вывод самостоятельно).
19. Производная показательной функций (вывод самостоятельно).
- Логарифмическое дифференцирование. Производная показательно-степенной функций (вывод).
- Неявные функции и их дифференцирование.
- Дифференциал функции, его геометрический смысл, основные свойства, инвариантность первого дифференциала.
- Параметрическая функция и её дифференцирование.
- Гиперболические функции и их дифференцирование (изучить самостоятельно)..
- Теоремы Ролля, Лагранжа, Коши (доказательства самостоятельно).
- Правило Лопиталя. Раскрытие неопределённостей
вида: 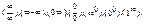
- Возрастание и убывание функции. Условия возрастания и убывания функции на интервале.
- Экстремум функции. Необходимое и достаточные условия существования.
- Точки перегиба графика функции, необходимый и достаточные признаки существования. Исследование функции на выпуклость и вогнутость графика.
- Асимптоты кривой. Уравнение наклонной асимптоты. Вертикальные асимптоты.
- Задача о наибольшем и наименьшем значениях функции на отрезке.
- Полная схема исследования функции и построение её графика.
- Приложения производной для решения задач физики, механики и других.
- ЗАМЕЧАНИЕ:
- Вопросы с 27 по 33 прорабатываются студентами самостоятельно, под руководством преподавателя, во время выполнения соответствующих индивидуальных заданий.






