Силы в ветвях цепной передачи.

Геометрические соотношения червячных передач.

Основная расчётная величина – осевой модуль червяка, равный торцевому модулю червячного колеса.

a_w = 0,5 ∙ (d₁ + d₂ +2∙x∙m) – межосевое расстояние;

d₁ и d₂ – делительные диаметры → d₁ = m ∙ q; d₂ = m ∙ z₂.

Передаточное отношение.

где

z₂ – число зубьев на червячном колесе;

z – число зубьев (заходов) червяка (заходов может быть равно 1, 2 или 4).

Большинство червячных передач выполняется смещением межосевого расстояния для получения стандартного его значения или изменением числа зубьев.

 

 

Геометрические соотношение цепных передач.

Межосевое расстояние а_опт = (30 ÷ 50) ∙ р.

Длина цепи .

Для нормальной работы цепи и исключения перенатяжения необходимо обеспечить провисание f.

Силы в зацеплении в червячных передач.

Fa1 = Ft2

При расчёте принимают, что сила приложена в полюсе зацепления по нормали к рабочей поверхности винта.

где η – КПД передачи; U – передаточноеотношение

 

 

 

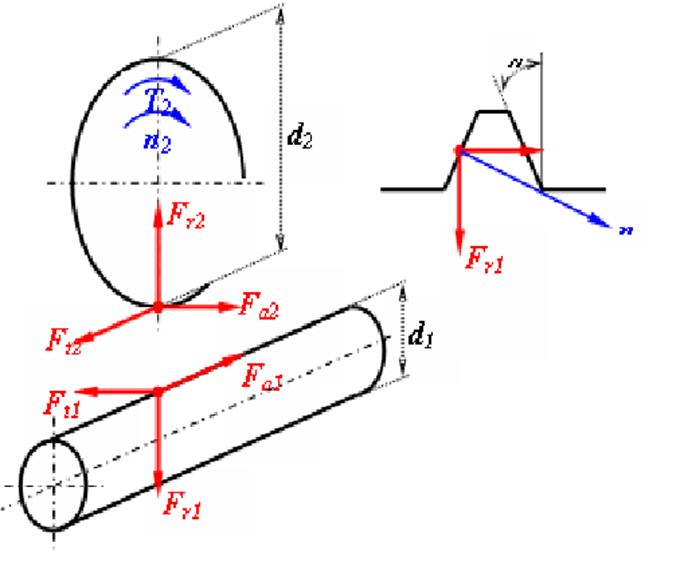
Расчет на прочность червячных передач.

Расчет на контактную прочность совмещен с этим расчетом путем выбора соответствующих контактных напряжений. Расчет контактных напряжений, от которых в основном и зависит износостойкость, проводится по формуле Герца:

Основные особенности - расчета червячных передач:

1.

2.

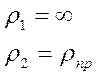
После подстановки в формулу Герца с учетом особенностей контакта червячных передач и дальнейших упрощений, получаем выражение:

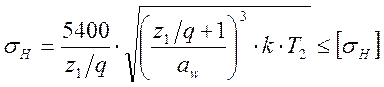(1), где

- коэффициент нагрузки учитывает неравномерность распределения нагрузки и динамичность нагрузки (ударность) .

зависит от коэффициента диаметра червяка и от режима нагрузки

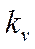- скорости скольжения и степени точности.

Проектный расчет проводится по формуле:

Эта формула получается, если в выражении (1) приравнять левую и правую части, а затем выразить одну из величин.

Силы в ветвях цепной передачи.

Окружная сила, передаваемая цепью – Ft = 2 T / d, d- диаметр делительной окружности звездочки. Предварительное натяжение цепи от провисания ведомой ветви F₀ = k_f q a g, где k_f – коэфф-т повисания. q – масса 1 м цепи [кг\м] по табл. а – межосевое расстояние [м]. g = 9.81 [м\с²]

Натяжение цепи от центробежных сил Fv = q v ². Сила Fv нагружает звенья цепи по всему ее контуру, но звездочками не воспринимается.

Натяжение ведущей ветви цепи работающей передачи F₁ = F_t + F₀ + F_v Натяжение ведомой ветви цепи F₂ равно большему из натяжений F₀ и F_v

Нагрузка на вала звездочек. Цепь действует с силой Fn = k_BF_t +2 F₀

k_B – коэф-т нагрузи вала

 

 

Межосевое расстояние а_опт = (30 ÷ 50) ∙ р.

Длина цепи .

Нагрузки на вал.

F = k ∙ F_t + 2 ∙ F₀, где k – коэфф-т нагрузки на вал; F_t – усилие в тяговой ветви в цепи; F₀ – предварительное натяжение цепи, обусловленное её провисанием.

F2

1) окружная сила ;

2) предварительное натяжение от провисания F₀ = K_f ∙ q ∙ a ∙ g, где

K_f – коэфф-т, учитывающий расположение передачи в пространстве

(K_f = 6, если α = 0º, K_f = 1, если α = 90º); a – площадь попереч. сечения цепи;