Отношения и отображения
Задача 3. Для бинарного отношения  ,
,  , заданного матрицей
, заданного матрицей 
a) проверьте выполнимость свойств рефлексивности, симметричности, транзитивности,
b) найдите отношение инверсии  и композицию
и композицию 
1.  . 2.
. 2.  .
.
3. 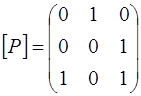 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
Задача 4. Укажите два инъективных, но не сюръективных, два сюръективных, но не инъективных и два биективных отображения множеств  и
и 
1.  .
.
2. 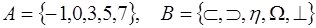 .
.
3.  .
.
4.  .
.
5.  .
.
6. 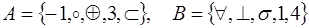 .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15. 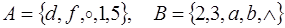 .
.
16.  .
.
17. 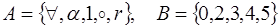 .
.
18.  .
.
19.  .
.
20.  .
.
Комбинаторика
Задача 5.
1. Сколько различных слов можно получить перестановкой букв слова «атаман», при условии, что согласные идут в алфавитном порядке, но буквы «а» не стоят рядом?
2. Сколько различных слов можно получить перестановкой букв слова «ворон», при условии, что две буквы «о» не стоят рядом?
3. Сколько различных слов можно получить перестановкой букв слова «пастух», при условии, что между двумя гласными расположены две согласные буквы?
4. Сколько различных слов можно получить перестановкой букв слова «криминал», при условии, что пятое и седьмое места заняты согласными буквами?
5. Сколько различных слов можно получить перестановкой букв слова «перешеек», при условии, что четыре буквы «е» не идут подряд?
6. Сколько различных слов можно получить перестановкой букв слова «диктатура», при условии, что как гласные, так и согласные буквы идут в алфавитном порядке?
7. Сколько различных слов можно получить перестановкой букв слова «катастрофа», при условии, что не меняется порядок согласных букв?
8. Сколько различных слов можно получить перестановкой букв слова «парламент», при условии, что согласные идут в алфавитном порядке, гласные буквы – в порядке, обратном алфавитному?
9. Сколько различных слов можно получить перестановкой букв слова «телефон», при условии, что в начале и в конце слова стоит согласная буква?
10. Сколько различных слов можно получить перестановкой букв слова «президент», при условии, что согласные идут в алфавитном порядке?
11. Сколько различных слов можно получить перестановкой букв слова «полномочия», при условии, что никакие гласные буквы не стоят рядом?
12. Сколько различных слов можно получить перестановкой букв слова «логарифм», при условии, что второе, четвертое и шестое места заняты согласными буквами?
13. Сколько различных слов можно получить перестановкой букв слова «переворот», при условии, что не больше одной пары одинаковых букв стоят рядом?
14. Сколько различных слов можно получить перестановкой букв слова «ультиматум», при условии, что между буквами «т» стоят все гласные буквы и только они?
15. Сколько различных слов можно получить перестановкой букв слова «комитет», при условии, что гласные буквы не стоят рядом и разделяются буквами «т»?
16. Сколько различных слов можно получить перестановкой букв слова «зоология», при условии, что три буквы «о» стоят рядом?
17. Сколько различных слов можно получить перестановкой букв слова «непоседа», при условии, что согласные и гласные буквы чередуются?
18. Сколько различных слов можно получить перестановкой букв слова «салфетка», при условии, что запрещено буквосочетание «алт»?
19. Сколько различных слов можно получить перестановкой букв слова «взломать», при условии, что между двумя гласными находятся три согласные буквы?
20. Сколько различных слов можно получить перестановкой букв слова «институт», при условии, что одинаковые буквы не идут друг за другом?
Задача 6. Вычислите значение 6-го члена числовой последовательности, заданной рекуррентным соотношением
Варианты 1-10:  ,
,
Варианты 11-20:  .
.
| № | 1,11 | 2,12 | 3,13 | 4,14 | 5,15 | 6,16 | 7,17 | 8,18 | 9,19 | 10,20 |

| -2 | -3 | ||||||||

| -1 | -1 | -3 |
Задача 7. Найти общее решение рекуррентного соотношения 5-го порядка
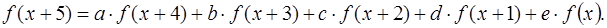
Варианты:
| № | a | b | c | d | e |
| 1 | -8 | -33 | -18 | ||
| 2 | -11 | -30 | -75 | ||
| 3 | -4 | -13 | -6 | ||
| 4 | -26 | -32 | |||
| 5 | -27 | -12 | |||
| 6 | -11 | -8 | |||
| 7 | -7 | -19 | |||
| 8 | -83 | -216 | |||
| 9 | -2 | -14 | |||
| 10 | -4 | -16 | -16 | ||
| 11 | -2 | -4 | -24 | ||
| 12 | -2 | ||||
| 13 | -6 | -6 | -18 | ||
| 14 | -6 | -45 | -27 | ||
| 15 | -70 | -40 | |||
| 16 | -1 | ||||
| 17 | -4 | -57 | -36 | ||
| 18 | -34 | -24 | |||
| 19 | -40 | -16 | |||
| 20 | -2 | -33 |
Булевы функции
Задача 8. Запишите КНФ и ДНФ булевой функции с помощью тождественных преобразований. Проверьте по таблице истинности.
1. 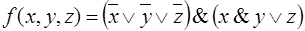 .
.
2.  .
.
3.  .
.
4. 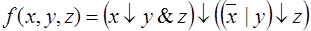 .
.
5.  .
.
6. 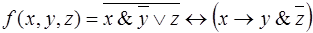 .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11. 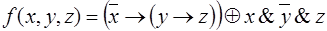 .
.
12. 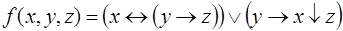 .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19. 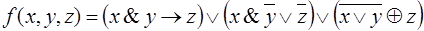 .
.
20.  .
.
Графы
Задача 9. Запишите матрицу смежности графа. Запишите матрицу кратчайших путей между вершинами графа. Найдите путь максимальной пропускной способности графа. Найдите максимальный поток в сети.
Вариант 1.

Вариант 2.

Вариант 3.

Вариант 4.

Вариант 5.

Вариант 6.
















Задача 10. Решите вырожденную закрытую транспортную задачу венгерским методом.
Математическая логика и теория алгоритмов
Задача 11. Докажите справедливость утверждения по методу резолюций.
1. Если бы он ей не сказал, то она бы и не узнала. Если бы она не спросила, то он и не сказал ей. Она узнала. Значит, она спросила.
2. Если из того, что на грядке выросло много морковки следует, что если поливать грядку раствором табачной пыли, то никакие насекомые не сядут на рассаду. Грядку поливали раствором табачной пыли. Значит если на грядке много морковки, то на рассаду не сели никакие насекомые.
Задача 12. Выполните сколемизацию формулы исчисления предикатов.
1.  .
.
2.  .
.
3. 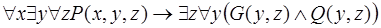 .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15. 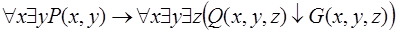 .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20.  .
.
Задача 13. Запишите нормальный алгоритм Маркова и программу для машины Тьюринга вычисления функции  .
.
Варианты 1-10: 
Варианты 11-20: 
| № | 1,11 | 2,12 | 3,13 | 4,14 | 5,15 | 6,16 | 7,17 | 8,18 | 9,19 | 10,20 |

| ||||||||||

|






