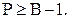Прямым произведением 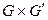 графов
графов  и
и  называется граф, у которого
называется граф, у которого 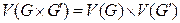 (т.е. вершины имеют вид
(т.е. вершины имеют вид 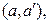 где
где 
 причём
причём
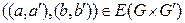

 (3)
(3)
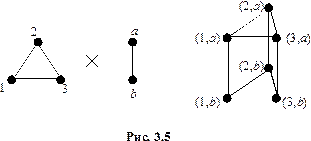
 соединены ребром в точности в следующих случаях: а)
соединены ребром в точности в следующих случаях: а) 
 б)
б) 
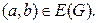
Например, если 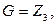
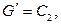 то графом
то графом 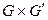 будет являться треугольная призма (см. рис. 3.5).
будет являться треугольная призма (см. рис. 3.5).
Для графического построения графа 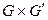 следует нарисовать граф
следует нарисовать граф  а затем каждую из вершин “раздуть” до графа
а затем каждую из вершин “раздуть” до графа 
Упражнение 3.5. Изобразить граф 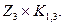
Решение (см. рис. 3.6).
 Нарисуем граф
Нарисуем граф  с вершинами большого размера – для того, чтобы заменить каждую из них графом
с вершинами большого размера – для того, чтобы заменить каждую из них графом  Соединение вершин осуществляется по правилу (3).
Соединение вершин осуществляется по правилу (3).
Граф 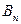 (п - мерный куб). Его вершинами являются строчки
(п - мерный куб). Его вершинами являются строчки 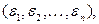 где
где 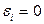 или 1. Две вершины
или 1. Две вершины  и
и 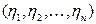 соединены ребром в том и только том случае, если строчки
соединены ребром в том и только том случае, если строчки  и
и 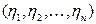 имеют отличие ровно в одной позиции, т.е. существует такое
имеют отличие ровно в одной позиции, т.е. существует такое  что
что  и
и 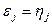 при
при  На рисунке 3.7 изображены графы
На рисунке 3.7 изображены графы  и
и 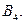
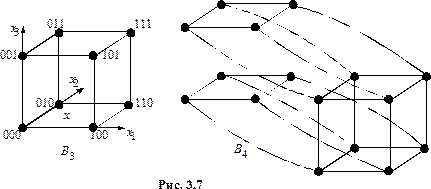
Для упрощения обозначений в записи вершин мы не пишем скобки и запятые, т.е. пишем 110 вместо 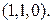
Упражнение 3.6. Найти количество вершин и рёбер графа 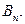
Решение. Так как вершины графа 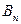 – это строчки
– это строчки  и
и 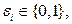 то всего вершин
то всего вершин  Далее, для вершины
Далее, для вершины  можно получить
можно получить  смежных с ней вершин, меняя поочерёдно каждую компоненту
смежных с ней вершин, меняя поочерёдно каждую компоненту 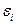 на противоположную
на противоположную 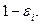 Следовательно, из каждой вершины исходит ровно
Следовательно, из каждой вершины исходит ровно  рёбер. Значит, общее количество рёбер равно
рёбер. Значит, общее количество рёбер равно  (деление на 2 делается ввиду того, что иначе каждое ребро было бы подсчитано дважды). Итак,
(деление на 2 делается ввиду того, что иначе каждое ребро было бы подсчитано дважды). Итак, 
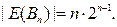
Подграф. Связный граф. Компоненты связности графа
Пусть  – граф. Понятие подграфа имеет два различных не эквивалентных между собой определения.
– граф. Понятие подграфа имеет два различных не эквивалентных между собой определения.
Подграф в широком смысле графа  – это граф
– это граф  где
где 

Подграф в узком смысле – это граф  где
где  и
и 
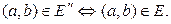
 Иными словами, для построения у графа
Иными словами, для построения у графа  подграфа в широком смысле надо выделить какое-либо множество вершин и некоторые из них соединить рёбрами, взятыми из графа
подграфа в широком смысле надо выделить какое-либо множество вершин и некоторые из них соединить рёбрами, взятыми из графа 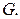 Для получения подграфа в узком смысле надо взять какое-либо множество вершин и соединить их в точности теми рёбрами, которыми они соединялись в графе
Для получения подграфа в узком смысле надо взять какое-либо множество вершин и соединить их в точности теми рёбрами, которыми они соединялись в графе 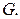 На рисунке 8 изображены графы
На рисунке 8 изображены графы  и
и  такие, что
такие, что  – подграф графа
– подграф графа  в широком, но не в узком смысле. Чтобы получить из него подграф в узком смысле, следует добавить ребро
в широком, но не в узком смысле. Чтобы получить из него подграф в узком смысле, следует добавить ребро 
Далее словом “подграф” мы будем называть подграф в широком смысле.
Граф  называется связным, если для любых двух его вершин
называется связным, если для любых двух его вершин  и
и  существует путь из
существует путь из  в
в  Будем считать, что из
Будем считать, что из  в
в  всегда существует путь нулевой длины (если длину определять по количеству рёбер). Любой граф
всегда существует путь нулевой длины (если длину определять по количеству рёбер). Любой граф  является объединением своих связных подграфов
является объединением своих связных подграфов  таких, что не существует рёбер (а значит, и путей), соединяющих вершины из разных
таких, что не существует рёбер (а значит, и путей), соединяющих вершины из разных  Эти подграфы называются компонентами связности графа
Эти подграфы называются компонентами связности графа 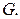
 Например, граф
Например, граф  изображённый на рисунке 3.9, состоит из трёх компонент связности.
изображённый на рисунке 3.9, состоит из трёх компонент связности.
У связного графа