В силу большого объема операций пользоваться изложенным выше алгоритмом практически невозможно. Разработано несколько экономичных методов построения минимальных ДНФ. Мы познакомимся с одним из них.
Выбранная нами для изучения методика построения минимальных ДНФ оперирует с несколькими видами дизъюнктивных нормальных форм. С двумя из них мы уже знакомы – это совершенная и минимальная дизъюнктивные нормальные формы. Рассмотрим еще две - сокращенную и тупиковую дизъюнктивные нормальные формы. Предварительно введем ряд новых понятий.
Определение. Элементарная конъюнкция называется импликантой функции  , если на любом наборе
, если на любом наборе  , на котором эта элементарная конъюнкция равна 1, функция
, на котором эта элементарная конъюнкция равна 1, функция  также обращается в 1.
также обращается в 1.
Очевидно, что каждая элементарная конъюнкция любой ДНФ, реализующей функцию  , является ее импликантой.
, является ее импликантой.
Определение. Будем называть импликанту функции  ее простой импликантой, если элементарная конъюнкция, получающаяся из нее удалением любой буквы, уже не является импликантой
ее простой импликантой, если элементарная конъюнкция, получающаяся из нее удалением любой буквы, уже не является импликантой  .
.
Упражнение 2.23. Перечислить все простые импликанты функции:
а)  ; б)
; б)  .
.
◄ а) Имеем 9 элементарных конъюнкций над переменными  : 1,
: 1,  ,
,  ,
,  ,
, 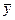 ,
,  ,
,  ,
,  ,
,  . Посмотрим, какие из них являются простыми импликантами функции
. Посмотрим, какие из них являются простыми импликантами функции  .
.

| 
| 
|
Константа 1 импликантой не является, так как на любом булевом векторе равна 1, в то время как  .
.
 обращается в 1 на наборах
обращается в 1 на наборах  и
и  , а
, а  , следовательно,
, следовательно,  не является импликантой
не является импликантой  .
.
 обращается в 1 на наборах
обращается в 1 на наборах  ,
,  , и на каждом из этих наборов
, и на каждом из этих наборов  также равна 1, следовательно,
также равна 1, следовательно,  – импликанта
– импликанта  . Эта импликанта простая, так как конъюнкция 1, полученная из нее путем удаления
. Эта импликанта простая, так как конъюнкция 1, полученная из нее путем удаления  , импликантой не является.
, импликантой не является.
 обращается в 1 на наборах
обращается в 1 на наборах  ,
,  , и на каждом из этих наборов
, и на каждом из этих наборов  также равна 1, следовательно,
также равна 1, следовательно,  – импликанта
– импликанта  . Эта импликанта простая, так как конъюнкция 1, полученная из нее путем удаления
. Эта импликанта простая, так как конъюнкция 1, полученная из нее путем удаления  , импликантой не является.
, импликантой не является.
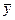 обращается в 1 на наборах
обращается в 1 на наборах  и
и  , а
, а  , следовательно,
, следовательно, 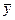 не является импликантой
не является импликантой  .
.
 обращается в 1 на одном наборе
обращается в 1 на одном наборе  , и
, и  , следовательно,
, следовательно,  – импликанта
– импликанта  . Однако простой эта импликанта не является, так как конъюнкция
. Однако простой эта импликанта не является, так как конъюнкция  , полученная из нее путем удаления буквы
, полученная из нее путем удаления буквы  , является импликантой.
, является импликантой.
 обращается в 1 на одном наборе
обращается в 1 на одном наборе  и
и  , следовательно,
, следовательно,  – импликанта
– импликанта  . Однако простой эта импликанта не является, поскольку конъюнкции
. Однако простой эта импликанта не является, поскольку конъюнкции  и
и  , полученные из нее путем удаления буквы
, полученные из нее путем удаления буквы  , являются импликантами.
, являются импликантами.
 обращается в 1 на наборе
обращается в 1 на наборе  , а
, а  , следовательно,
, следовательно,  не является импликантой
не является импликантой  .
.
 обращается в 1 на наборе
обращается в 1 на наборе  ,
,  , следовательно,
, следовательно,  импликанта
импликанта  . Однако простой эта импликанта не является, так как конъюнкция
. Однако простой эта импликанта не является, так как конъюнкция  , полученная из нее путем удаления
, полученная из нее путем удаления 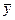 , является импликантой.
, является импликантой.
Таким образом, функция  имеет две простых импликанты
имеет две простых импликанты  и
и  .
.
б) решите самостоятельно. ►
Определение. Д изъюнкция всех простых импликант функции называется сокращенной ДНФ функции.
Например, для функции  (упр. 2.23 а)) сокращенная ДНФ имеет вид
(упр. 2.23 а)) сокращенная ДНФ имеет вид  .
.
Можно доказать, что сокращенная ДНФ функции  реализует функцию
реализует функцию  . Более того, в некоторых случаях функцию реализует дизъюнкция только некоторых (не всех!) простых импликант. В связи с этим уместно ввести понятие тупиковой ДНФ.
. Более того, в некоторых случаях функцию реализует дизъюнкция только некоторых (не всех!) простых импликант. В связи с этим уместно ввести понятие тупиковой ДНФ.
Определение. Тупиковой ДНФ функции называется такая реализующая ее дизъюнкция простых импликант, из которой нельзя удалить ни одну простую импликанту так, чтобы полученная после удаления ДНФ все еще реализовала функцию.
Отметим без доказательства следующий теоретический факт: минимальная ДНФ функции является тупиковой ДНФ.
Теперь, когда все необходимые понятия введены, мы можем наметить план построения минимальной ДНФ функции. План будет включать три этапа: на первом этапе строится сокращенная ДНФ функции, на втором – тупиковые ДНФ, на третьем – из тупиковых отбираются минимальные.




